大家都发表下对着俩曲线的理解吧。
分类、检索中的评价指标很多,Precision、Recall、Accuracy、F1、ROC、PR Curve......
一、历史
wiki上说,ROC曲线最先在二战中分析雷达信号,用来检测敌军。诱因是珍珠港事件;由于比较有用,慢慢用到了心理学、医学中的一些检测等应用,慢慢用到了机器学习、数据挖掘等领域中来了,用来评判分类、检测结果的好坏。
百科:ROC曲线指受试者工作特征曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系,它通过将连续变量设定出多个不同的临界值,从而计算出一系列敏感性和特异性,再以敏感性为纵坐标、(1-特异性)为横坐标绘制成曲线,曲线下面积越大,诊断准确性越高。在ROC曲线上,最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。
二、原理
这里就拿最经典的二分类(0、1)问题讨论吧,分类器分类之后,往往会得到对每个样本是哪一类的一个估计,像是LR模型就会将这个估计规范化到【0,1】,根据这个估计,你选择一个阈值p_0,就可以将分类结果映射到0,1了;分类效果好不好跟真实的label比比就行了。
所以你手里有decision和label两个向量,用来做分类结果的评估。
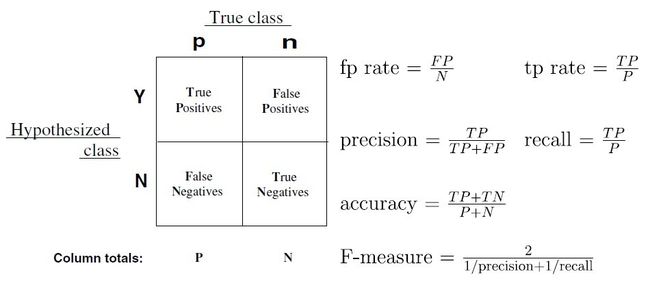
要看ROC的原理,总离不开上面这个表格,ROC绘制的就是在不同的阈值p_0下,TPR和FPR的点图。所以ROC曲线的点是由不同的p_0所造成的。所以你绘图的时候,就用不同的p_0采点就行。
Precision-Recall曲线,这个东西应该是来源于信息检索中对相关性的评价吧,precision就是你检索出来的结果中,相关的比率;recall就是你检索出来的结果中,相关的结果占数据库中所有相关结果的比率;所以PR曲线要是绘制的话,也是对cutoff进行遍历,这样也得到了不同的precision和recall的点。例如你选择了一个cutoff,从而根据cutoff判别分类的结果1或0。1就是检索返回的结果,0就是没有返回的结果。
数据库里有500条记录,其中50个是相关的(正样本),你通过一个cutoff,返回了75个1,其中只有45个是真正相关的;
那么在这个cutoff对应下的recall=45/50=0.9,precision=45/75=0.6。坐标就是(0.9,0.6),在这里绘制一个点吧。
可以看出TPR和Recall的形式是一样的,就是查全率了,FPR就是保证这样的查全率你所要付出的代价,就是把多少负样本也分成了正的了。
上面是我的理解,不知道对不对。
三、AUC的计算
为了更好的衡量ROC所表达结果的好坏,Area Under Curve(AUC)被提了出来,简单来说就是曲线右下角部分占正方形格子的面积比例;那么计算这个东西其实就很简单了,根据reference的paper,有很多很多计算方法,这里推荐一种近似采样的方法:采样。
你的分类器能够将正例排在负例前面的概率是多少,也就是采样中正例的decision>负例的decision的概率。
从stackoverflow上看到的代码,R语言:
|
1
2
3
4
5
6
|
auc <- mean(sample(pos.decision,1000,replace=T) > sample(neg.decision,1000,replace=T))
## or
aucs <- replicate(2000,mean(sample(pos.decision,1000,replace=T) > sample(neg.decision,1000,replace=T)))
auc2 <- round(mean(aucs),4)
|
其实这个可以等价于对于不规则图形的面积的采样估计了。谁能给推导一下?
四、ROC中最优的p_0的计算
简单理解下的话,保证TPR同时代价FPR要尽量的小,是不是可以建立max(TPR+(1-FPR))的模型,然后选p_0呢?
paper中有更加详细的方法。谁给详细介绍下?
五、ROC和PR曲线之间的关系和不同
当正负样本差距不大的情况下,ROC和PR的趋势是差不多的,但是当负样本很多的时候,两者就截然不同了,ROC效果依然看似很好,但是PR上反映效果一般,还需要继续努力啊。解释起来也简单,假设就1个正例,100个负例,那么基本上TPR可能一直维持在100左右,然后突然降到0.
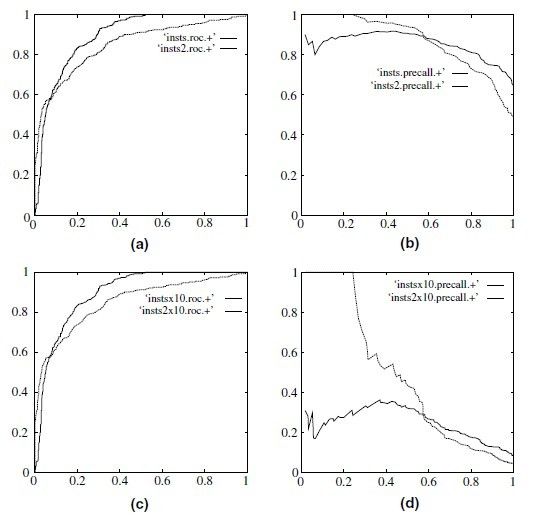
ROC and precision-recall curves under class skew. (a) ROC curves, 1:1; (b) precision-recall curves, 1:1; (c) ROC curves, 1:10 and (d) precisionrecall
六、具体例子和代码
(1)数据集
用的libsvm的那个270个样本的数据集,用LR模型做了一下:
0.688312721844616 1
0.461679176682519 0
0.405016268379421 1
0.693999977303342 0
0.391868684948981 0
0.526391961908057 0
0.570470938139219 1
0.708771207269333 1
0.700976655664182 1
0.713584109310541 1
0.545180177320974 0
0.646156295395112 0
0.347580513944893 0
0.391577777998607 1
....
(2)ROC曲线和PR曲线
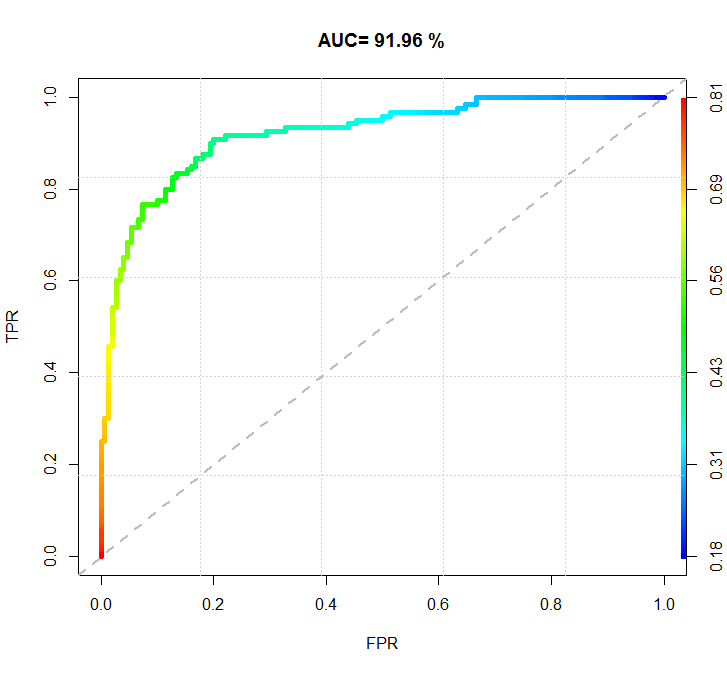
R语言的ROCR绘制的图形:
代码:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
|
library(ROCR)
a=read.table( "toy.txt" )
a <- as.matrix(a)
pred <- prediction(a[,1], a[,2])
perf <- performance(pred, "tpr" , "fpr" )
auc.tmp <- performance(pred, "auc" )
auc <- as.numeric([email protected])
auc <- round(auc, 4)
plot(perf,colorize=TRUE,lwd=5,xlab= "FPR" ,ylab= "TPR" , main=paste( "AUC=" ,auc*100, "%" ))
grid(5, 5, lwd = 1)
lines(par()$usr[1:2], par()$usr[3:4], lty=2, lwd=2, col= "grey" )
|
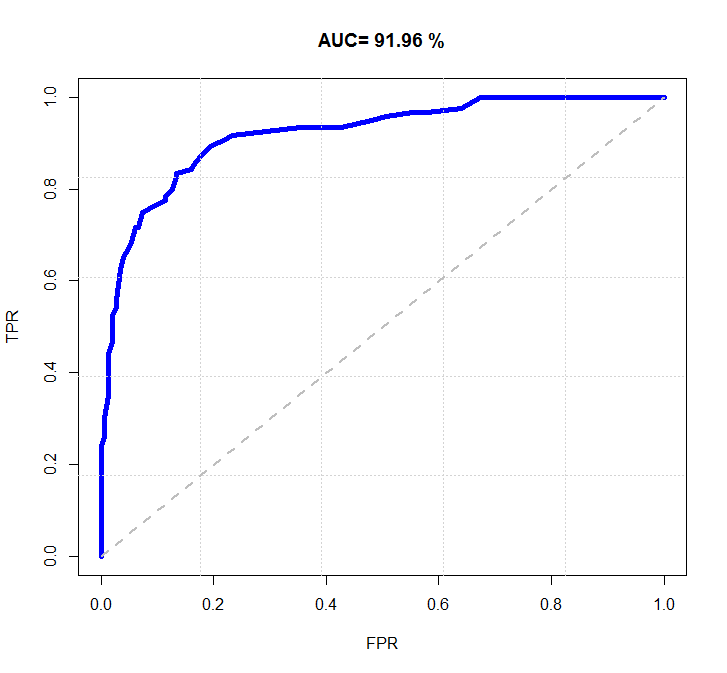
自己写代码绘制图像和估算AUC的值,AUC和ROCR包计算的还是很接近的:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
a <- read.table( "toy.txt" )
a <- as.matrix(a)
label <- a[,2]
decision <- a[,1]
ngrids <- 100
TPR <- rep(0, ngrids)
FPR <- rep(0, ngrids)
p0 <- rep(0, ngrids)
for (i in 1:ngrids)
{
p0[i] <- i/ngrids
pred_label <- 1*(decision > p0[i])
TPR[i] <- sum(pred_label * label) / sum(label)
FPR[i] <- sum(pred_label * (1-label)) / sum(1-label)
}
## compute AUC
pos.decision <- decision[which(label == 1)]
neg.decision <- decision[which(label == 0)]
auc <- mean(sample(pos.decision,1000,replace=T) > sample(neg.decision,1000,replace=T))
## or
aucs <- replicate(2000,mean(sample(pos.decision,1000,replace=T) > sample(neg.decision,1000,replace=T)))
auc2 <- round(mean(aucs),4)
plot(FPR, TPR, col=4,lwd=5, type= "l" , main=paste( "AUC=" ,auc2*100, "%" ))
grid(5, 5, lwd = 1)
points(c(0,1), c(0,1), type= "l" , lty=2, lwd=2, col= "grey" )
##
cut.op <- p0[which(TPR-FPR == max(TPR-FPR))]
|
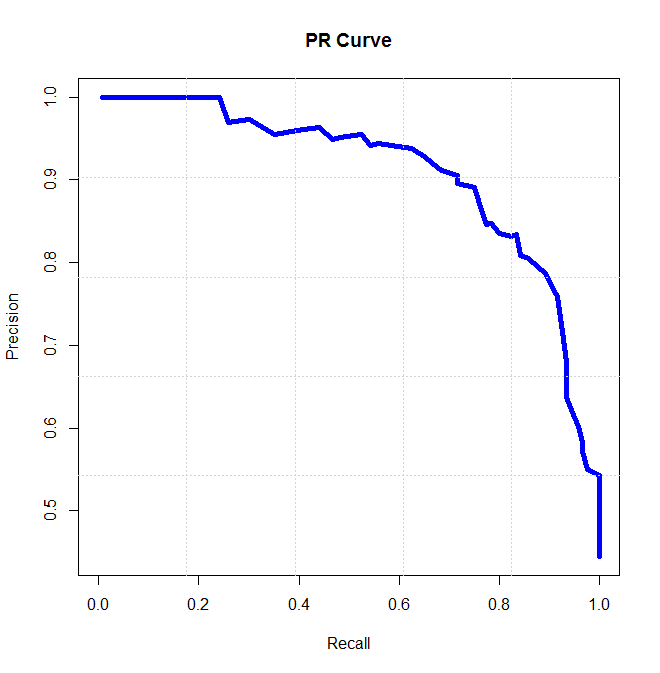
PR曲线:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
a <- read.table( "toy.txt" )
a <- as.matrix(a)
label <- a[,2]
decision <- a[,1]
ngrids <- 100
P <- rep(0, ngrids)
R <- rep(0, ngrids)
p0 <- rep(0, ngrids)
A <- rep(0, ngrids)
for (i in 0:ngrids)
{
p0[i] <- i/ngrids
pred_label <- 1*(decision > p0[i])
R[i] <- sum(pred_label * label) / sum(label)
P[i] <- sum(pred_label * label) / sum(pred_label)
A[i] <- sum((pred_label == label)*1)/nrow(a)
}
plot(R, P, col=4,lwd=5, type= "l" ,xlab= "Recall" ,ylab= "Precision" , main= "PR Curve" )
grid(5, 5, lwd = 1)
accuracy <- max(A)
|
七、Reference
[1]Tom Fawcett:An introduction to ROC analysis
[2]Jesse Davis,Mark Goadrich:The Relationship Between Precision-Recall and ROC Curves
[3]https://en.wikipedia.org/wiki/Receiver_operating_characteristic
[4]http://baike.baidu.com/view/42249.htm