Net: ConvTranspose2d

本文中主要讲解PyTorch中的转置卷积、逆卷积、微步卷积: ConvTranspose2d函数

ConvTranspose2d

nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)

此函数作一个反卷积操作，与Conv2d相反，此操作将图像的特征维度压缩，尺寸放大

输出的长和宽的计算
$$\begin{gathered} H_{out}=(H_{in}-1)\ast stride[0]-2\ast padding[0]+dilation[0]\ast (kernel\_size[0]-1)+outpu{t}_{p}adding[0]+1 \\ {W}_{out}=(W_{in}-1)\ast stride[1]-2\ast padding[1]+dilation[1]\ast (kernel\_size[1]-1)+outpu{t}_{p}adding[1]+1 \end{gathered}$$

参数的含义

• in_channels ([int]) – 输入图像通道数
• out_channels ([int])– 输出图像通道数
• kernel_size ([int] or [tuple]) – 卷积核的大小
• stride ([int] or [tuple], optional) – 输入图片之间的间隔. Default: 1
• padding ([int], [tuple]or [str], optional) – 卷积核与输入边缘相交的pixel. Default: 0（即相交一个单位）
• output_padding ([int] or [tuple], optional) – Additional size added to one side of each dimension in the output shape. Default: 0
• groups ([int], optional) – Number of blocked connections from input channels to output channels. Default: 1
• bias ([bool], optional) – If True, adds a learnable bias to the output. Default: True
• dilation ([int] or [tuple], optional) – Spacing between kernel elements. Default: 1

注意：这里的padding和stride与Conv2d的不同

• padding：卷积核向中心移动的步数，即当padding为0时，卷积核在卷积的时候移动到最边缘时与输入相交一个单位，当padding为1时，卷积核在卷积的时候移动到最边缘时与输入相交两个单位，即向内部多移动了一个单位
• stride：输入彼此之间的距离，stride默认为1，即输入之间彼此相距一个单位，当stride为2时，输入之间会额外散开一个单位，即输入之间相距两个单位（即任意一个输入pixel需要移动两次才能到达最近的pixel）

ConvTranspose2d是Conv2d的逆操作，当不知道如何使用时，可以直接将参数设为：你的Conv2d的参数如何，ConvTranspose2d的参数不变就可以回到最初输入时的状态

当然我们不能不知道他的原理，在假设已知Conv2d如何操作的基础上，我们通过三个例子来介绍一下ConvTranspose2d的具体操作过程，图源GitHub

实例1: stride=1 padding=0

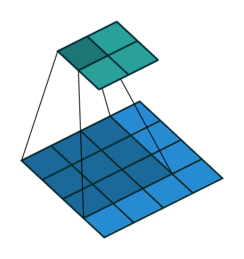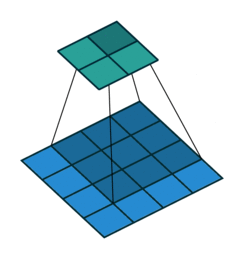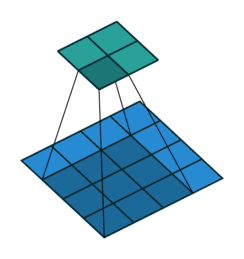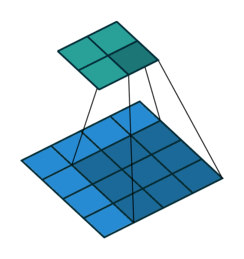
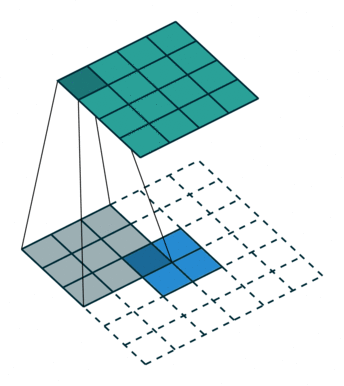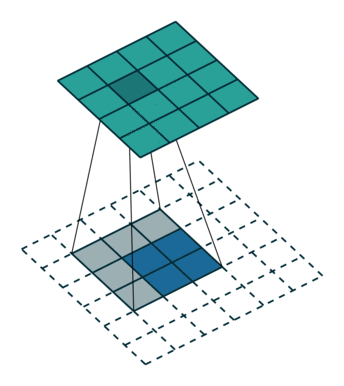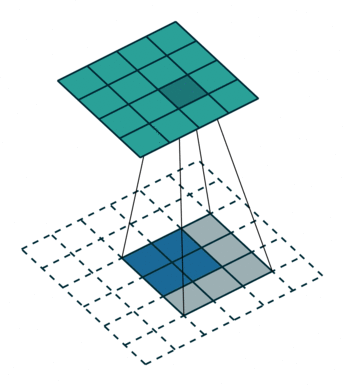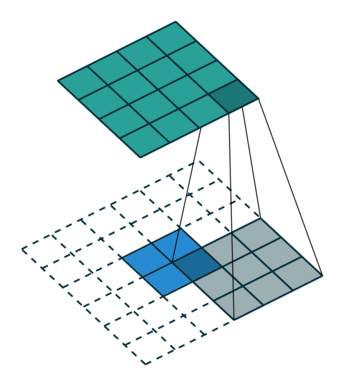
在默认情况下ConvTranspose2d将feature map进行kernal size-1的padding

看以下例子，(4, 4)的图片经过Conv变成了(2, 2)，当我们对他进行stride=1，padding=0的ConTranspose2d的时候，默认已经进行了kernel size-1=2的padding操作，然后其他不变：kernel size=3，stride=1和padding=0

# input
input = torch.ones((1, 1, 4, 4), dtype=torch.float)
# conv
conv = nn.Conv2d(1, 1, 3, stride=1, padding=0, bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
output = conv(input)
# convTranspose
trans = nn.ConvTranspose2d(1, 1, 3, stride=1, padding=0, bias=False)
trans.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
trans(output)
'''
input---------------------
tensor([[[[1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.]]]])
conv ---------------------
tensor([[[[9., 9.],
          [9., 9.]]]], grad_fn=)
trans---------------------
tensor([[[[ 9., 18., 18.,  9.],
          [18., 36., 36., 18.],
          [18., 36., 36., 18.],
          [ 9., 18., 18.,  9.]]]], grad_fn=)
'''

实例2: stride=2 padding=0

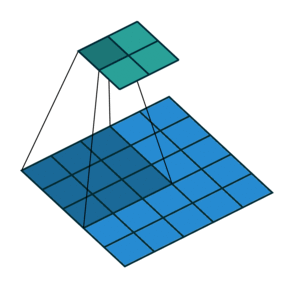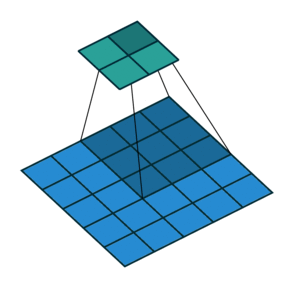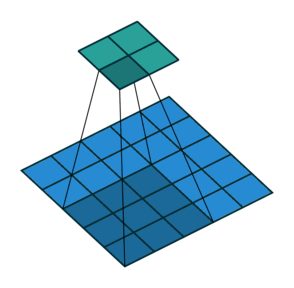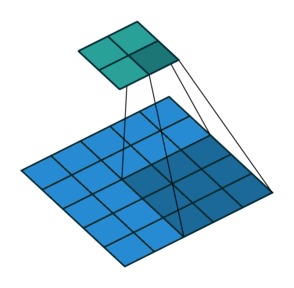
这里我们将stride从1变为2，如下图所示，对于Conv来说他的变化是卷积核移动的距离变为2，对于ConvTranspose来说变化是feature map中像素之间的距离+1，而默认的kernal size-1的padding不变

# input
input = torch.ones((1, 1, 5, 5), dtype=torch.float)
# conv
conv = nn.Conv2d(1, 1, 3, stride=2, padding=0, bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
output = conv(input)
# convTranspose
'''
input---------------------
tensor([[[[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]]]])
conv ---------------------
tensor([[[[9., 9.],
          [9., 9.]]]], grad_fn=)
trans---------------------
tensor([[[[ 9.,  9., 18.,  9.,  9.],
          [ 9.,  9., 18.,  9.,  9.],
          [18., 18., 36., 18., 18.],
          [ 9.,  9., 18.,  9.,  9.],
          [ 9.,  9., 18.,  9.,  9.]]]], grad_fn=)
'''

实例3: stride=1 padding=1

我们将stride不变，padding变为1，对于Conv来说每条边加入了填充，我们看一下对于ConvTranspose的变化，默认的我们对其进行kernal size-1的填充，这里本应该填充为2，但是由于我们的padding=1，所以我们的填充为2-1=1即只进行1个填充

# input
input = torch.ones((1, 1, 5, 5), dtype=torch.float)
# conv
conv = nn.Conv2d(1, 1, 3, stride=1, padding=1, bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
output = conv(input)
# convTranspose
trans = nn.ConvTranspose2d(1, 1, 3, stride=1, padding=1, bias=False)
trans.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
'''
input---------------------
tensor([[[[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]]]])
conv ---------------------
tensor([[[[4., 6., 6., 6., 4.],
          [6., 9., 9., 9., 6.],
          [6., 9., 9., 9., 6.],
          [6., 9., 9., 9., 6.],
          [4., 6., 6., 6., 4.]]]], grad_fn=)
trans---------------------
tensor([[[[25., 40., 45., 40., 25.],
          [40., 64., 72., 64., 40.],
          [45., 72., 81., 72., 45.],
          [40., 64., 72., 64., 40.],
          [25., 40., 45., 40., 25.]]]], grad_fn=)
'''

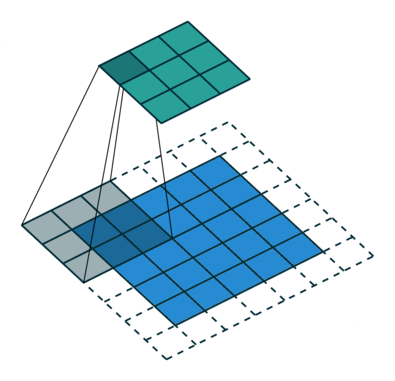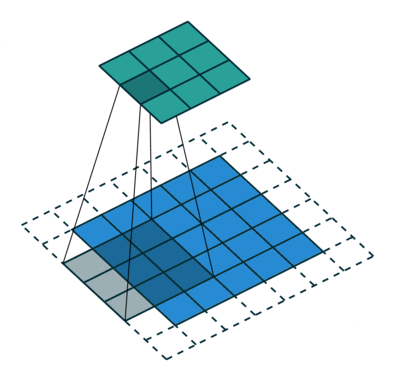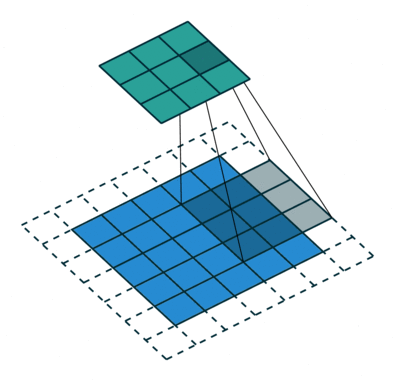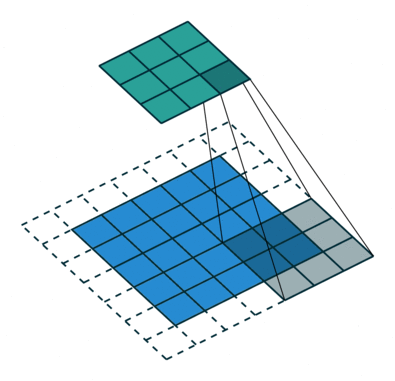
实例4: stride=2 padding=1

这里我们融合了实例2和实例3的特点：既包含了stride的变化也包含了padding的变化，直接看图，对于Conv我们很容易理解，对于ConvTranspose，stride依旧是将feature map的像素之间距离+1，padding也像上面例子一样，本身默认的填充是kernal size-1=2，这里变为2-1=1，然后填充区域是在feature map分开之后的基础上进行的

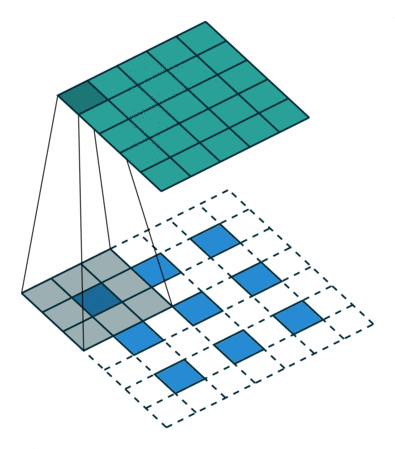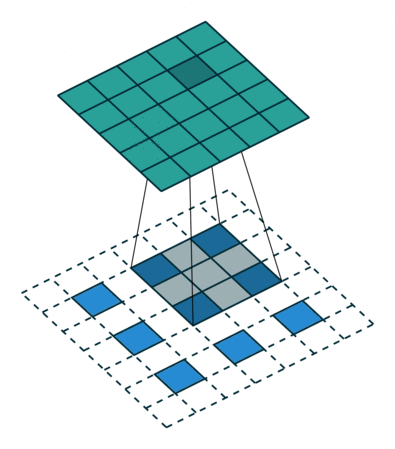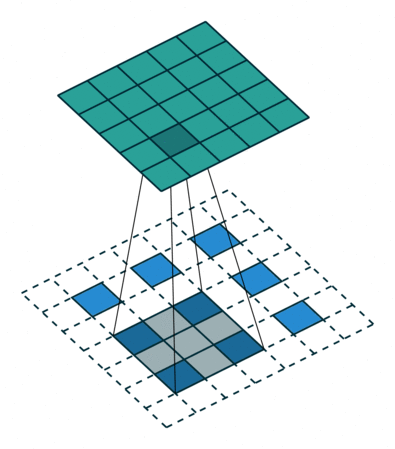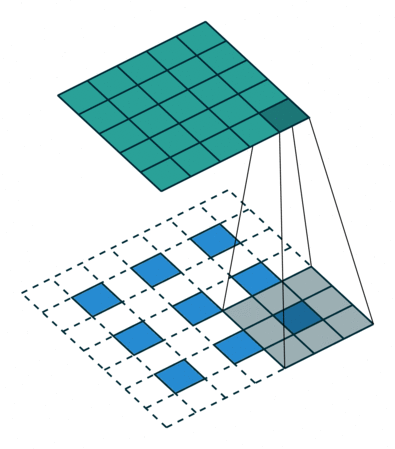实例总结

经过上面的例子我们可以了解到以下参数

• stride=1 padding=0: 此情况下，对于Conv表示步长为1，填充为0，而对于ConvTranspose则为feature map不变的情况下进行默认的kernal size-1的padding
• stride：对于Conv就是卷积核移动的距离，对于ConvTranspose是输入的feature map的像素之间的间隔
• padding: 对于Conv是原图四条边填充的大小，对于ConvTranspose本身默认填充kernal size-1，现在变为kernel size-1-padding
• in_channels out_channels kernel_size: Conv与ConvTranspose相同

output_padding

我的一个简单理解是：output padding用来保证通过ConvTranspose之后生成的特征图和通过Conv之前输出的特征图的维度相同
Feature_in → Conv Other Operation ConvTranspose → Feature_out
其中size(feature_in) = size(feature_out)

在ConvTranspose2d中有一个output_padding参数，这里给出Stack Overflow的解释

这里简单讲解一下，就是说对于两个相同的输入一个为(7, 7)，一个为(8, 8)，当我们对他进行Conv操作时得到的feature map大小相同均为(3, 3)

# input
input1 = torch.ones((1, 1, 7, 7), dtype=torch.float)
input2 = torch.ones((1, 1, 8, 8), dtype=torch.float)
# conv
conv = nn.Conv2d(1, 1, 3, stride=2, bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
conv(input1)
conv(input2)
'''
conv ---------------------
tensor([[[[9., 9., 9.],
          [9., 9., 9.],
          [9., 9., 9.]]]], grad_fn=)
conv ---------------------
tensor([[[[9., 9., 9.],
          [9., 9., 9.],
          [9., 9., 9.]]]], grad_fn=)
'''

但是如果我们想将它们恢复到原来的大小怎么办呢？如果我们将输出的(3, 3)的feature map直接输入到ConvTranspose中输出是(7, 7)的图片，如果我们想输出(8, 8)的怎么办呢？就要用到output padding方法，从下面例子我们可以看出，output padding将最终的输出进行了补零操作**(其实我没看到文档中说的怎么做的，只是从例子中看到的是补零)**

# no output padding
trans1 = nn.ConvTranspose2d(1, 1, 3, stride=2, bias=False)
trans1.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
trans1(output)
# with output padding
trans2 = nn.ConvTranspose2d(1, 1, 3, stride=2, output_padding=1, bias=False)
trans2.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
trans2(output)
'''
tensor([[[[ 9.,  9., 18.,  9., 18.,  9.,  9.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.],
          [18., 18., 36., 18., 36., 18., 18.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.],
          [18., 18., 36., 18., 36., 18., 18.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.]]]], 
          grad_fn=)
tensor([[[[ 9.,  9., 18.,  9., 18.,  9.,  9.,  0.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.,  0.],
          [18., 18., 36., 18., 36., 18., 18.,  0.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.,  0.],
          [18., 18., 36., 18., 36., 18., 18.,  0.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.,  0.],
          [ 9.,  9., 18.,  9., 18.,  9.,  9.,  0.],
          [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.]]]], 
          grad_fn=)
'''