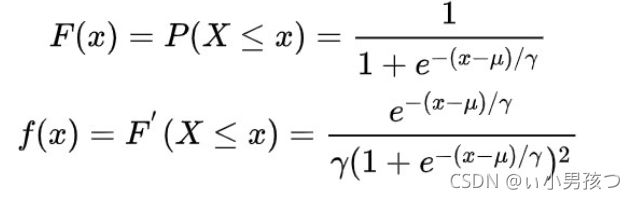【机器学习实验五】逻辑斯蒂回归
目录
一、逻辑斯蒂回归基本概念
1.1、基本概念
1.2、特点
1.3、Logistic分布
1.4、逻辑斯蒂回归模型
二、利用逻辑斯蒂模型进行分类测试
2.1、数据准备
2.2、编写代码查看数据集的分布情况
2.3、训练分类算法
2.4、绘制决策边界
三、从疝气病症状预测病马的死亡率
3.1、项目背景
3.2、数据准备
3.3、使用Python构建logistics分类器
四、总结
4.1、Logistic回归的一般过程:
4.2、优缺点
一、逻辑斯蒂回归基本概念
1.1、基本概念
逻辑斯蒂(Logistic)回归又称为“对数几率回归”,虽然名字有回归,但是实际上却是一种经典的分类方法,其主要思想是:根据现有数据对分类边界线(Decision Boundary)建立回归公式,以此进行分类。
1.2、特点
- 优点:计算代价不高,具有可解释性,易于实现。不仅可以预测出类别,而且可以得到近似概率预测,对许多需要利用概率辅助决策的任务很有用。
- 缺点:容易欠拟合,分类精度可能不高。
- 适用数据类型:数值型和标称型数据。
1.3、Logistic分布
Logistic 分布是一种连续型的概率分布,其分布函数和密度函数分别为:
其中,μ 表示位置参数,γ 为形状参数。我们可以看下逻辑斯蒂分布在不同的![]() 、
、![]() 的情况下,其概率密度函数
的情况下,其概率密度函数![]() 的图形:
的图形:
逻辑斯蒂分布在不同的![]() 、
、![]() 的情况下,其概率分布函数
的情况下,其概率分布函数![]() 的图形:
的图形:
Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似,但是 Logistic 分布的尾部更长,所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在μ=0,γ=1 的特殊形式。
1.4、逻辑斯蒂回归模型
逻辑斯蒂回归模型是一种分类模型,由条件概率分布P(Y|X)表示,形式为参数化的逻辑斯蒂分布。这里随机变量X取值为实数,随机变量Y取值为1或0。
二项逻辑斯谛回归模型是如下的条件概率分布:
这里x属于实数,Y属于{0,1}是输出,w和b是参数,w称为权值向量,b称为偏置,w*x为w和x的内积。
对于给定的输入实例x,按照上述分布函数可以求得P(Y=1|x)和P(Y=0|x)。逻辑斯谛回归是比较两个条件概率值的大小,将实例x分到概率值大的那一类。
有时候为了方便,将权值向量和输入向量加以扩充,仍记作w,x,即
这时,逻辑斯蒂回归模型如下:
得到上面的回归模型了,上面的回归模型中有一个未知参数w,在利用上述的模型对数据进行预测之前需要先求取参数w的值,这里采用极大似然估计的方法求取参数w。
假设:
可以得到似然函数为:
对似然函数取对数可得:
这样问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降法或者梯度上升法。
将利用极大似然估计得到的w值代入上述的模型中,即可用于测试数据集的预测。
二、利用逻辑斯蒂模型进行分类测试
2.1、数据准备
如图所示,该数据有两个特征维度,我们可以将第一列看作x轴的值,第二列看作y轴的值,第三列为分类的标签。
2.2、编写代码查看数据集的分布情况
# -*- coding:UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:加载数据
Returns:
dataMat - 数据列表
labelMat - 标签列表
"""
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
"""
函数说明:绘制数据集
"""
def plotDataSet():
dataMat, labelMat = loadDataSet() #加载数据集
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord1, ycord1, s = 20, c = 'black', marker = 's',alpha=.5)#绘制正样本
ax.scatter(xcord2, ycord2, s = 20, c = 'red',alpha=.5) #绘制负样本
plt.title('DataSet') #绘制title
plt.xlabel('x'); plt.ylabel('y') #绘制label
plt.show() #显示
if __name__ == '__main__':
plotDataSet()
如图所示:假设Sigmoid函数的输入记为z,那么z=w0x0 + w1x1 + w2x2,即可将数据分割开。其中,x0为全是1的向量,x1为数据集的第一列数据,x2为数据集的第二列数据。因此,我们需要求出这个方程未知的参数w0,w1,w2,也就是我们需要求的回归系数(最优参数)。
2.3、训练分类算法
# -*- coding:UTF-8 -*-
import numpy as np
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
"""
函数说明:sigmoid函数
Parameters:
inX - 数据
Returns:
sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
函数说明:梯度上升算法
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
"""
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组,返回权重数组
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
print(gradAscent(dataMat, labelMat))
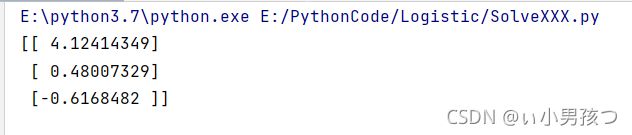
运行结果:
现在,我们已经求出了未知的参数w0,w1,w2,接下去通过求解出的参数,我们就可以确定不同类别数据之间的分隔线,画出决策边界。
2.4、绘制决策边界
# -*- coding:UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:加载数据
Parameters:
无
Returns:
dataMat - 数据列表
labelMat - 标签列表
"""
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
"""
函数说明:sigmoid函数
Parameters:
inX - 数据
Returns:
sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
函数说明:梯度上升算法
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
"""
def plotDataSet():
dataMat, labelMat = loadDataSet() #加载数据集
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5) #绘制负样本
plt.title('DataSet') #绘制title
plt.xlabel('x'); plt.ylabel('y') #绘制label
plt.show()
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组,返回权重数组
"""
函数说明:绘制数据集
Parameters:
weights - 权重参数数组
"""
def plotBestFit(weights):
dataMat, labelMat = loadDataSet() #加载数据集
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord1, ycord1, s = 20, c = 'black', marker = 's',alpha=.5)#绘制正样本
ax.scatter(xcord2, ycord2, s = 20, c = 'red',alpha=.5) #绘制负样本
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit') #绘制title
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
plotDataSet()
weights = gradAscent(dataMat, labelMat)
plotBestFit(weights)
由运行结果可得,通过我们求解的参数确定的分类模型来划分数据类别取得了很好的效果。
三、从疝气病症状预测病马的死亡率
3.1、项目背景
本次项目将使用Logistic回归来预测患疝气病的马的存活问题。 原始数据集如下图所示:
这里的数据包含了368个样本和28个特征。这种病不一定源自马的肠胃问题,其他问题也可能引发马疝病。该数据集中包含了医院检测马疝病的一些指标,有的指标比较主观,有的指标难以测量,例如马的疼痛级别。
3.2、数据准备
上述数据还存在一个问题,数据集中有30%的值是缺失的。数据中的缺失值是一个非常棘手的问题,下面给出了一些可选的做法:
- 使用可用特征的均值来填补缺失值;
- 使用特殊值来填补缺失值,如-1;
- 忽略有缺失值的样本;
- 使用相似样本的均值添补缺失值;
- 使用另外的机器学习算法预测缺失值。
数据预处理
- 如果测试集中一条数据的特征值已经确实,那么我们选择实数0来替换所有缺失值,因为本文使用Logistic回归。因此这样做不会影响回归系数的值。sigmoid(0)=0.5,即它对结果的预测不具有任何倾向性。
- 如果测试集中一条数据的类别标签已经缺失,那么我们将该类别数据丢弃,因为类别标签与特征不同,很难确定采用某个合适的值来替换。
3.3、使用Python构建logistics分类器
# -*- coding:UTF-8 -*-
import numpy as np
import random
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.01 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组,并返回
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
def colicTest():
frTrain = open('horseColicTraining.txt') #打开训练集
frTest = open('horseColicTest.txt') #打开测试集
trainingSet = []; trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine)-1):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[-1]))
trainWeights = gradAscent(np.array(trainingSet), trainingLabels) #使用改进的随即上升梯度训练
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(len(currLine)-1):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainWeights[:,0]))!= int(currLine[-1]):
errorCount += 1
errorRate = (float(errorCount)/numTestVec) * 100 #错误率计算
print("测试集错误率为: %.2f%%" % errorRate)
def classifyVector(inX, weights):
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
if __name__ == '__main__':
colicTest()可以看到由于数据集中存在 30%的值是缺失的,因此测试集的错误率会比较高,这是很难避免的。
四、总结
4.1、Logistic回归的一般过程:
- 收集数据:采用任意方法收集数据。
- 准备数据:由于需要进行距离计算,因此要求数据类型为数值型。另外,结构化数据格式则最佳。
- 分析数据:采用任意方法对数据进行分析。
- 训练算法:大部分时间将用于训练,训练的目的是为了找到最佳的分类回归系数。
- 测试算法:一旦训练步骤完成,分类将会很快。
- 使用算法:首先,我们需要输入一些数据,并将其转换成对应的结构化数值;接着,基于训练好的回归系数,就可以对这些数值进行简单的回归计算,判定它们属于哪个类别;在这之后,我们就可以在输出的类别上做一些其他分析工作。
4.2、优缺点
优点:实现简单,易于理解和实现;计算代价不高,速度很快,存储资源低。
缺点:容易欠拟合,分类精度可能不高。