逻辑回归算法(Logistic Regression)原理(含多项逻辑斯蒂回归对参数求偏导的推导过程)及numpy代码实现

逻辑回归算法，虽然名字中带有“回归”二字，但解决的却是分类问题，它与线性回归之间有什么样的关系呢？

1.二项逻辑斯蒂回归

概述

二项逻辑斯蒂回归，简称逻辑回归，又称为对数几率回归，是一种二分类模型。
模型：$$h=\frac{1}{1+e^{-(W^{T}x+b)}}$$代价函数：$$J=-\frac{1}{m}\sum _{i=1}^m{y}_i{\ln }_{}h(x_i)+(1-y_i){\ln }_{}\left[1-h(x_i)\right]$$目标：$$W^{\ast },b^{\ast }=\underset{W,b}{\mathrm{argmin}}J(W,b)$$

模型形式——对数几率函数

考虑这样一个问题：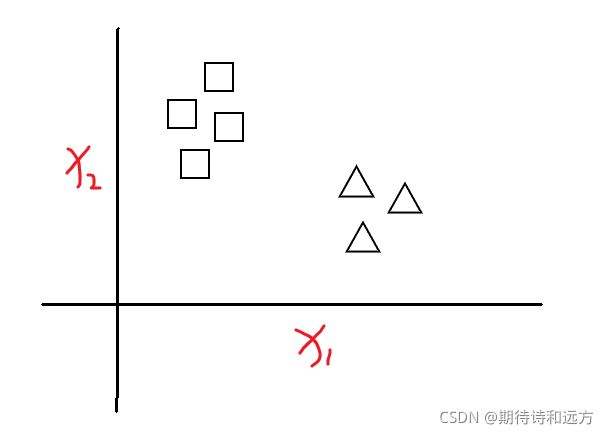
假设一组数据的分布如上图所示，建立一个什么样的模型将两个类别区分开来呢？线性回归模型$z=W^{T}x+b$貌似可以解决这个问题，但是线性回归模型的输出值是一个实值，而二分类任务的输出标记$y\in \left\{0,1\right\}$（在二项逻辑斯蒂回归中，我们强制将正类标记为1，负类标记为0，后面将会提到这样做的原因），于是，我们考虑将实值$z$转换为0/1值，最理想的是单位阶跃函数$y=\{\begin{array}{ll}0& \text{ if }z<0\\ 0.5& \text{ if }z=0\\ 1& \text{ if }z>0\end{array}$.但单位阶跃函数是不连续的，我们希望找到在一定程度上接近单位阶跃函数的替代函数，并希望它单调可微，对数几率函数正是这样一个常用的替代函数，对数几率函数（又叫sigmod函数，logistic函数）：$$y=\frac{1}{1+e^{-z}}$$

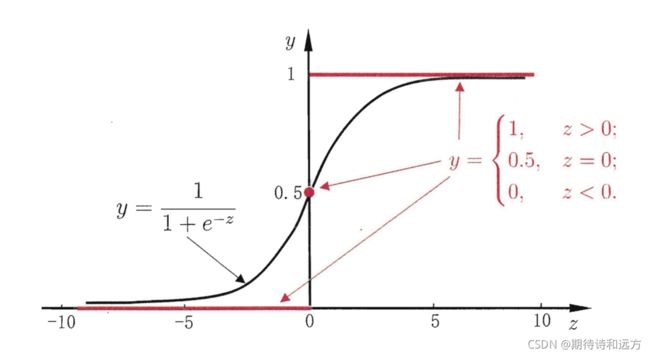
这样就把实数域的值转化到了$(0,1)$。
综上，得到逻辑回归模型形式：$$h=\frac{1}{1+e^{-(W^{T}x+b)}}$$值域在(0, 1)之间，并且正类标记为1，负类标记为0，所以y可以看作$x$是正类的概率。
分类决策：当$y>0.5$时，判断为正类，$y<0.5$时，判断为负类，$y=0.5$时，可以任意判别。

模型参数估计——最大似然估计

负平均对数似然函数

如何来估计模型的参数呢？我们需要定义模型的代价函数，线性回归模型使用的平方误差代价函数应用于逻辑回归模型中将是非凸函数，不能保证找到全局最小值，在逻辑回归模型中，我们使用负平均对数似然函数。

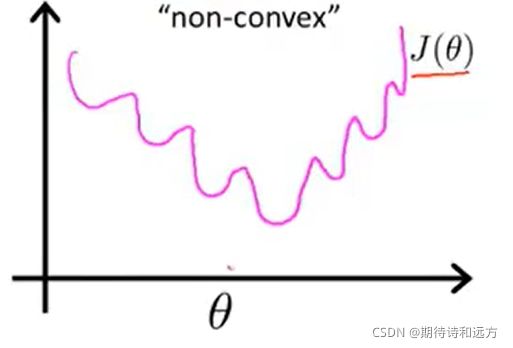
似然函数：一种关于模型中的参数的函数，$L(\theta |x)=P(X=x|\theta )$.
负平均对数似然函数就是在似然函数的基础上取对数再求平均再加上负号。

下面我们来推导一下样本集中$m$个独立样本出现的似然函数：
训练样本集$\left\{(x_i,y_i),i=1,2,\dots ,m\right\}$，假设样本彼此独立，类别标记$y\in \left\{0,1\right\}$，则样本$(x_i,y_i)$出现的概率：$$P(x_i,y_i)={\left[P(y_i=1|x_i)\right]}^{y_i}{\left[1-P(y_i=1|x_i)\right]}^{1-y_i}P(x_i),$$$m$个独立样本出现的似然函数为：$$\begin{array}{rl}l& =\prod _{i=1}^{m}P(x_i,y_i)\\ & =\prod _{i=1}^m{\left[P(y_i=1|x_i)\right]}^{y_i}{\left[1-P(y_i=1|x_i)\right]}^{1-y_i}P(x_i)\\ & =\prod _{i=1}^m{\left[P(y_i=1|x_i)\right]}^{y_i}{\left[1-P(y_i=1|x_i)\right]}^{1-y_i}\prod _{i=1}^{m}P(x_i)\end{array}$$其中${\prod }_{i=1}^{m}P(x_i)$与模型参数无关，所以似然函数可简化为$$l=\prod _{i=1}^m{\left[P(y_i=1|x_i)\right]}^{y_i}{\left[1-P(y_i=1|x_i)\right]}^{1-y_i}$$公式中存在很多连乘，为了计算简便，我们考虑对似然函数取对数：$$\begin{array}{rl}{l}^{\prime }={\ln }_{}l& ={\ln }_{}\left\{\prod _{i=1}^m{\left[P(y_i=1|x_i)\right]}^{y_i}{\left[1-P(y_i=1|x_i)\right]}^{1-y_i}\right\}\\ & =\sum _{i=1}^m{\ln }_{}\left\{{\left[P(y_i=1|x_i)\right]}^{y_i}{\left[1-P(y_i=1|x_i)\right]}^{1-y_i}\right\}\\ & =\sum _{i=1}^m{y}_i{\ln }_{}\left[P(y_i=1|x_i)\right]+(1-y_i){\ln }_{}\left[1-P(y_i=1|x_i)\right]\end{array}$$平均对数似然函数为：$$\hat{l}=\frac{1}{m}\sum _{i=1}^m{y}_i{\ln }_{}\left[P(y_i=1|x_i)\right]+(1-y_i){\ln }_{}\left[1-P(y_i=1|x_i)\right]$$
目标：最大化平均对数似然求解参数：$\underset{w,b}{arg\max \hat{l}}$
等价于：最小化负的平均对数似然：$\underset{w,b}{\mathrm{argmax}}(\widehat{-l})$，这样，就可以使用梯度下降法求解参数了。

使用梯度下降法求解参数

使用梯度下降法求解参数的关键是求得代价函数对参数的偏导，下面来推导一下：（前面的一篇文章单独讲了梯度下降法，不了解的可以看一下：梯度下降法求解最优化问题）
$$\begin{array}{rl}J& =-\frac{1}{m}\sum _{i=1}^m{y}_i{\ln }_{}h(x_i)+(1-y_i){\ln }_{}\left[1-h(x_i)\right]\\ h& =\frac{1}{1+e^{-z}}\\ z& =w^{T}x+b\\ \frac{\partial h}{\partial z}& =\frac{0-e^{-z}\ast (-1)}{(1+e^{-z}{)}^2}=\frac{e^{-z}}{(1+e^{-z}{)}^2}=h(1-h)\\ \frac{\partial J}{\partial w_j}& =\frac{\partial J}{\partial h}\cdot \frac{\partial h}{\partial z}\cdot \frac{\partial z}{\partial w_j}\\ & =-\frac{1}{m}\sum _{i=1}^m(\frac{y_i}{h(x_i)}+\frac{1-y_i}{1-h(x_i)})\cdot h(x_i)(1-h(x_i))\cdot x_i^{(j)}\\ & =-\frac{1}{m}\sum _{i=1}^m(y_i-h(x_i))x_i^{(j)}\\ & =\frac{1}{m}\sum _{i=1}^m(h(x_i)-y_i)x_i^{(j)},(j=1,2,\dots n)\\ \frac{\partial J}{\partial b}& =\frac{\partial J}{\partial h}\cdot \frac{\partial h}{\partial z}\cdot \frac{\partial z}{\partial b}\\ & =-\frac{1}{m}\sum _{i=1}^m(\frac{y_i}{h(x_i)}+\frac{1-y_i}{1-h(x_i)})\cdot h(x_i)(1-h(x_i))\cdot 1\\ & =-\frac{1}{m}\sum _{i=1}^m(y_i-h(x_i))\\ & =\frac{1}{m}\sum _{i=1}^m(h(x_i)-y_i)\end{array}$$将参数$b$与$w$向量合并为一个向量，$b$即$w_0$，$x_i^0$始终为1，所以代价函数$J$对参数$w_j$的偏导可以写为：$$\frac{\partial J}{\partial w_j}=\frac{1}{m}\sum _{i=1}^m(h(x_i)-y_i)x_i^{(j)},(j=0,1,2,\dots n)$$梯度下降法参数更新：
repeat until convergence{
$w_j:=w_j-\alpha {\sum }_{i=1}^m(h(x_i)-y_i)x_i^{(j)}$
(simultaneously update all ${\theta }_j$)
}

特征缩放

特征缩放加速收敛。给数据做如下变化：$$x_i{}^{\prime }=\frac{x_i-\mu }{s},$$其中$\mu$为均值向量，$s=\{\begin{array}{c}各个特征的max-min构成的向量\\ 标准差向量\end{array}$.
注：$x_0$不需要进行缩放，$x_0=1$.

代码实现

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split

def load_data():
    dataset = datasets.load_breast_cancer()
    dataX = dataset.data
    dataY = dataset.target
    print("dataX的shape:", dataX.shape)
    return dataX, dataY

def normalization(dataX):
    '''z-score归一化
    Parameters:
        dataX: 输入特征向量
    Returns:
        dataX1: 归一化之后的dataX
        mu: 均值向量
        sigma: 标准差向量
    '''
    mu = dataX.mean(0)
    sigma = dataX.std(0)
    dataX1 = (dataX - mu) / sigma
    return dataX1, mu, sigma

class logistic_regression():
    def __init__(self, dataX, dataY, alpha=0.1):
        self.datasize = dataX.shape[0]
        # 给dataX矩阵第一列补1，用于和偏置值计算
        ones = np.ones(self.datasize)
        self.dataX = np.c_[ones, dataX] # 补完1之后的dataX
        self.dataY = dataY
        self.alpha = alpha
        self.theta = np.zeros(self.dataX.shape[1]) # 参数初始化
        
    def fit(self):
        iterations = 100 # 设置停止迭代规则，迭代iterations次就停止更新
        for i in range(iterations):
            updated_theta = [] # 更新之后的参数，暂存到updated_theta列表中
            # 计算y_hat, y = 1 / (1 + e^(-z))
            y_hat = []
            z = np.dot(self.dataX, self.theta)
            for zi in z:
                # 需要考虑z的正负问题，z为负数，-z为正数，-z是e的指数，太大的话会导致内存溢出，需要做出修改
                if zi < 0:
                    y = np.exp(zi) / (np.exp(zi) + 1)
                else:
                    y = 1 / (1 + np.exp(-zi))
                y_hat.append(y)
            y_hat = np.array(y_hat)
            loss = -1 / self.datasize * np.sum(self.dataY * np.log(y_hat + 1e-5) + (1 - self.dataY) * np.log(1 - y_hat + 1e-5))
            print('第', i, '次迭代的loss:', loss)
            # 依次计算theta_j更新后的值
            for j, theta_j in enumerate(self.theta):
                xj = self.dataX[:, j]
                updated_theta_j = theta_j - self.alpha * np.sum((y_hat - self.dataY) * xj)
                updated_theta.append(updated_theta_j)
            self.theta = updated_theta # 所有参数计算完之后再一起更新
        print('训练完成！')
        
    def predict(self, testX, testY):
        ones = np.ones(testX.shape[0])
        testX = np.c_[ones, testX]
        z = np.dot(testX, self.theta)
        y_hat = []
        for zi in z:
            if zi < 0:
                y = np.exp(zi) / (np.exp(zi) + 1)
            else:
                y = 1 / (1 + np.exp(-zi))
            label = 1 if y >= 0.5 else 0
            y_hat.append(label)
        y_hat = np.array(y_hat)
        cnt = 0
        n = len(testY)
        for i in range(n):
            if y_hat[i] == testY[i]:
                cnt += 1
        print('模型预测正确率：', cnt / n)
        return y_hat

if __name__ == "__main__":
    # 1.获取数据集
    dataX, dataY = load_data()
    # 2.划分数据集
    trainX, testX, trainY, testY = train_test_split(dataX, dataY, test_size=0.3, random_state=0)
    # 3.标准化预处理
    newTrainX, mu, sigma = normalization(trainX)
    print('mu =', mu, "sigma =", sigma)
    newTestX = (testX - mu) / sigma
    # 4.构建一个逻辑回归模型
    model = logistic_regression(newTrainX, trainY)
    # 5.训练模型
    model.fit()
    # 6.测试模型
    y_hat = model.predict(newTestX, testY)
    # 7.输出预测值与真实值的差距
    print("预测值：", y_hat)
    print("真实值：", testY)

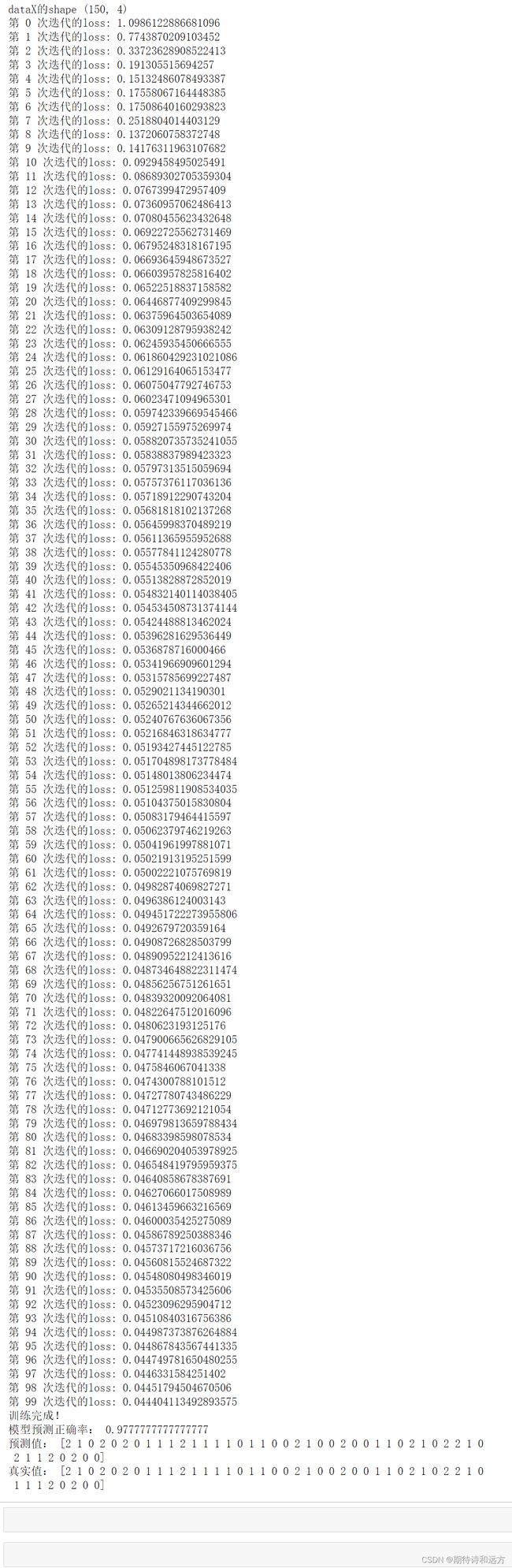
代码运行结果：

2.多项逻辑斯蒂回归

概述

多项逻辑斯蒂回归又称为softmax回归，是二项逻辑斯蒂回归的推广，用于多类别分类。
模型：$y_j=\frac{e^{z_j}}{{\sum }_{i=1}^C{e}^{z_i}}$即softmax函数形式（softmax函数的推导详见参考文献1），将$z_j=w_j^{T}x+b_j$带入，得到：$$P(y=j|x)=\frac{e^{w_j^{T}x+b_j}}{{\sum }_{i=1}^C{e}^{w_i^{T}x+b_i}},j=1,2,\dots ,C$$同样使用最大似然函数可得代价函数：$$J=-\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^C\left[{\ln }_{}P(y_i|x_i{)}^{I(y_i=k)}\right]$$目标：$$W^{\ast },b^{\ast }=\underset{W,b}{\mathrm{argmin}}J(W,b),$$得到C组参数。

梯度下降法求解

下面推导一下代价函数$J$对$w_j$的偏导，这里的$w_j$是一个向量，并且偏置值$b$也包含在其中。(推导过程我搞了两三天没求出来，最终还是多亏了向大佬求助)$$\begin{array}{rl}J& =-\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^C\left[{\ln }_{}P(y_i|x_i{)}^{I(y_i=j)}\right]\\ P(y=i|x)& =P_i=\frac{e^{z_i}}{{\sum }_{l=1}^C{e}^{z_l}}\\ z_i& =w_i^{T}x\\ \frac{\partial P}{\partial z_k}& =\{\begin{array}{ll}\frac{e^{z_k}\ast {\sum }_{l=1}^C{e}^{z_l}-e^{z_k}\ast e^{z_k}}{({\sum }_{l=1}^C{e}^{z_l}{)}^2}=P_k-P_k^2& \text{ if }i=k\\ \frac{0-e^{z_i}\ast e^{z_k}}{({\sum }_{l=1}^C{e}^{z_l}{)}^2}=-P_i{P}_k& \text{ if }i\ne k\end{array}\\ \frac{\partial J}{\partial w_k}& =\frac{\partial J}{\partial P}\cdot \frac{\partial P}{\partial z}\cdot \frac{\partial z}{\partial w_k}\\ & =-\frac{1}{m}\sum _{i=1}^m\left[I(y_i=k)\frac{1}{P_k}\cdot (P_k-P_k^2)+\sum _{j=1,j\ne k}^{C}I(y_i=j)\frac{1}{P_j}\cdot (-P_j{P}_k)\right]\cdot x_i\\ & =-\frac{1}{m}\sum _{i=1}^m\left[I(y_i=k)-I(y_i=k)P_k-P_k\sum _{j=1,j\ne k}^{C}I(y_i=j)\right]\cdot x_i\\ & =-\frac{1}{m}\sum _{i=1}^m\left[I(y_i=k)-I(y_i=k)P_k-P_k(1-I(y_i=k))\right]\cdot x_i\\ & =-\frac{1}{m}\sum _{i=1}^m\left[I(y_i=k)-P_k\right]\cdot x_i\end{array}$$
参数更新：
repeat until convergence{
$w_k:=w_k+\alpha {\sum }_{i=1}^{m}I(y_i=k)(1-P(y_i=k|x_i))\cdot x_i$
(simultaneously update all $w_j$)
}

代码实现

以下是使用多项逻辑斯蒂回归算法实现鸢尾花类别分类的代码。

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split

def load_data():
    dataset = datasets.load_iris()
    dataX = dataset.data
    dataY = dataset.target
    print('dataX的shape', dataX.shape)
    return dataX, dataY

def normalization(dataX):
    '''z-score归一化
    Parameters:
        dataX: 输入特征向量
    Returns:
        dataX1: 归一化之后的dataX
        mu: 均值向量
        sigma: 标准差向量
    '''
    mu = dataX.mean(0)
    sigma = dataX.std(0)
    dataX1 = (dataX - mu) / sigma
    return dataX1, mu, sigma

def dense_to_onehot(dense, n_classes):
    '''将类别标号转为onehot向量
    Parameters:
        dense: 稠密的类别向量
        n_classes: 类别数目
    Returns:
        onehot: 类别向量独热编码后的矩阵
    注：此函数写的较为简单，只适用于类别从0开始编号，且依次递增1的情况
    '''
    n_labels = dense.shape[0]
    onehot = np.zeros((n_labels, n_classes))
    for i in range(n_labels):
        onehot[i, dense[i]] = 1
    return onehot

class multinomial_logistic_regression():
    def __init__(self, dataX, dataY, alpha=0.1):
        self.datasize = dataX.shape[0] # 样本数
        self.n_classes = len(set(dataY)) # 类别数
        # 给dataX矩阵第一列补1，用于和偏置值计算
        ones = np.ones(self.datasize)
        self.dataX = np.c_[ones, dataX] # 补完1之后的dataX
        self.dataY = dense_to_onehot(dataY, self.n_classes) # 将标签转为onehot向量
        self.alpha = alpha # 学习率
        self.theta = np.zeros((self.dataX.shape[1], self.n_classes)) # 参数初始化
        
    def softmax(self, z):
        '''softmax函数
        Parameters:
            z: shape(m, c)
        Returns:
            y: shape(m, c)
        '''
        y = np.zeros(z.shape)
        for i, z_i in enumerate(z):
            l = np.array([(lambda num: np.exp(z_ij) if z_ij < 0 else (1 / np.exp(-z_ij)))(z_ij) for z_ij in z_i]) # a如果是正数，作为e的指数可能会溢出，所以e^a转换为1 / e^(-a)
            l = l / sum(l)
            y[i] = l
        return y
    
    def fit(self):
        iterations = 100 # 设置停止迭代规则，迭代iterations次就停止更新
        for iteration in range(iterations):
            # 计算y_hat
            z = np.dot(self.dataX, self.theta) # dataX(m, n) theta(n, c) 结果为(m, c)
            y_hat = self.softmax(z)
            # 计算损失
            loss = -1 / self.datasize * np.sum(np.log(np.sum(np.multiply(y_hat, self.dataY), axis=1)))
            print('第', iteration, '次迭代的loss:', loss)
            # 更新theta
            updated_theta = np.zeros(self.theta.shape) # 更新之后的参数，暂存到updated_theta列表中
            for j in range(self.n_classes):
                temp = (self.dataY[:, j] - y_hat[:, j]).reshape((self.datasize, 1))
                theta_j = self.theta[:, j] + self.alpha * np.sum(np.multiply(temp, self.dataX), axis=0) 
                updated_theta[:, j] = theta_j
            self.theta = updated_theta
        print('训练完成！')
        
    def predict(self, testX, testY):
        ones = np.ones(testX.shape[0])
        testX = np.c_[ones, testX]
        z = np.dot(testX, self.theta)
        y_hat = np.argmax(z, axis=1)
        cnt = 0
        n = len(testY)
        for i in range(n):
            if y_hat[i] == testY[i]:
                cnt += 1
        print('模型预测正确率：', cnt / n)
        return y_hat

if __name__ == "__main__":
    # 1.获取数据集
    dataX, dataY = load_data()
    # 2.划分数据集
    trainX, testX, trainY, testY = train_test_split(dataX, dataY, test_size=0.3, random_state=0)
    # 3.标准化预处理
    newTrainX, mu, sigma = normalization(trainX)
    newTestX = (testX - mu) / sigma
    # 4.构建一个逻辑回归模型
    model = multinomial_logistic_regression(newTrainX, trainY)
    # 5.训练模型
    model.fit()
    # 6.测试模型
    y_hat = model.predict(newTestX, testY)
    # 7.输出预测值与真实值的差距
    print("预测值：", y_hat)
    print("真实值：", testY)

代码执行结果：

3.总结

以上就是逻辑斯蒂回归的全部内容了，推导过程有些复杂，希望大家可以自己推导一下。

参考文献：
1.多类别逻辑回归（Multinomial Logistic Regression）