【模式识别】C++实现K-means算法
一、问题描述
试用K均值法对如下模式分布进行聚类分析:
{x1(0, 0),x2(3,8),x3(2,2),x4(1,1),x5(5,3),x6(4,8),x7(6,3),x8(5,4),x9(6,4),x10(7,5)}
二、算法介绍
对于本次算法程序,我将其分为以下几个部分:
1、变量定义:
这里定义了一个名为Node数据结构,其中包括两个元素:element(用于记录各个模式样本的数据)、kinds(用于记录每个模式样本所属的类别,该数据为0时代表该模式样本尚未分类)。
#define Number 100 //模式样本的最大维数与个数
struct Node //定义了一个用于存放模式样本的数据结构
{
double element[Number] = { 0 };//模式样本
int kinds = 0; //模式样本所属类别,0为未分类状态
} X[Number];2、数据的输入与算法初始化:
由用户输入模式样本,并将其放在一个名为node的Node类型数组里。然后接受用户输入的k值(用户想将样本分为几类),并对k值的合法性进行了检测,确保后续算法运行的正确性。
/* 数据的输入与初始化 */
int n; //模式样本的维数
int m; //模式样本的个数
cout << "请输入需要分类的模式样本的维数:";
cin >> n;
cout << "请输入需要分类的模式样本的个数:";
cin >> m;
/*接受用户手动输入的模式样本的维数与个数,用于之后使用。*/
cout << "请输入需要分类的模式样本:\n";
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
cin >> X[i].element[j];
}
}
int k; //用于K-means算法的k值
while (1)
{
cout << "请输入本次聚类分析需要将模式样本分成的类数(k值):";
cin >> k;
if (k <= 1)
cout << "k值需为大于等于1的整数";
else
break;
}3、初始化聚类中心:
根据用户之前输入的数据,初始化聚类中心,做好迭代计算准备。
/* 根据用户输入的k值初始化聚类中心 */
Node* Z = new Node[k]; //聚类中心
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
Z[i].element[j] = X[i].element[j];
}
}4、迭代计算聚类中心:
将迭代计算所需要的全部数据传入迭代计算函数(Kmeans)中进行计算。
/* 迭代计算聚类中心 */
Kmeans(k,X,Z,m,n);5、输出计算结果:
算法运行结束后输出对应的计算结果,并清空程序运行期间占用的内存。
/* 输出计算结果 */
cout << "经过计算\n";
for (int i = 0; i < k; i++)
{
cout << "聚类中心Z" << i + 1 << "=( ";
for (int j = 0; j < n; j++)
{
cout << Z[i].element[j] << " ";
}
cout << ")\n";
}6、迭代函数Kmeans:
迭代函数Kmeans是本次实验的主要问题,将在该部分对其进行详细介绍。
定义迭代过程变量:
void Kmeans(int k, Node X[], Node Z[], int m, int n) //K-means算法中迭代计算函数
{
int number = 0; //用于记录迭代计算轮数
double* D = new double[k]; //用于存放迭代计算中距离的变量
int* N = new int[k](); //用于统计每个模式类中的模式样本数
int(*S)[100] = new int[k][100]; //用于统计每个模式类中的模式样本
int condition = 1; //算法结束的条件在算法开始前,首先定义了一些用于迭代过程的变量它们的功能分别如下:
number:用于记录迭代轮数,方便计算过程中的屏幕输出。
D:double类型的数组,大小为k,可以存放某次迭代计算过程中某个模式样本与各个聚类中心的距离。
N:int类型的数组,大小为k,可以存放在某次迭代计算中每个模式样本中的模式样本数。
S:int类型的二维数组,大小为k*100,用于存放k个模式类中的模式样本分别有那些。
condition:用于判断迭代计算是否结束,0为还需迭代计算,1为迭代计算完成,被初始化为1。
迭代计算(以下内容全部在一个while循环中)
每次迭代计算开始时进行数据的初始化(迭代次数加一,迭代结束条件置1)将Ni初始化为0,防止二义性。
这里是一个两层循环,最外层循环的意思是遍历每个模式样本(共有m个)。内层第一个for循环是通过调用Distance函数来计算某个模式样本与各个聚类中心(共k个)的欧氏距离,并将这个距离按计算顺序存放在数组D中。内层第二个for循环是通过对数组D的遍历来寻找某个模式样本与聚类中心的最短距离,并通过改变该模式样本的kinds的内容来表示将该模式样本划分到对应模式类下。
while (1) //迭代运算
{
number++;
condition = 1;
for (int i = 0; i < k; i++) //对Ni进行初始化
{
N[i] = 0;
}
/* 分别计算各点与聚类中心的距离 */
for (int i = 0; i < m; i++)
{
for (int j = 0; j < k; j++)
{
D[j] = Distance(X[i], Z[j], n);
}
int temp = 0;
for (int j = 0; j < k; j++)
{
if (D[temp] > D[j])
temp = j;
X[i].kinds = temp + 1;
}
}下图是Distance函数的定义。
double Distance(Node X, Node Z, int n) //欧式距离计算函数
{
double result = 0;
for (int i = 0; i < n; i++)
{
result = result + (X.element[i] - Z.element[i]) * (X.element[i] - Z.element[i]);
}
result = sqrt(result);
return result;
}模式样本的输出和记录
接下来通过一个两层循环对前一步划分好模式类的模式样本进行输出和记录。
本次循环的最外层要循环k次,代表一个聚类中心循环一次,在一次循环中在内层循环部分逐个访问了所有模式样本,通过比对该模式样本的kinds来确认该模式样本是否属于这个模式类。若属于,则将该模式类的长度记录变量N[i]加一,然后记录下这个模式样本的编号(记录在二维数组S中)。
/* 统计每个模式类中的样本数和样本 */
for (int i = 0; i < k; i++)
{
cout << "第" << number << "次迭代计算后,模式类" << i + 1 << "中包括{ ";
int temp = 0;
for (int j = 0; j < m; j++)
{
if (X[j].kinds == (i + 1))
{
N[i]++;
S[i][temp] = j;
cout << "X" << S[i][temp] + 1 << " ";
temp++;
}
}
cout << "}\n";
}计算新的聚类中心
接下来通过重新分类的模式样本的数据,计算新的聚类中心。
在此之前将上次迭代计算的聚类中心保存到oldZ中以便之后使用。
在聚类中心计算时,调用Add函数来实现矩阵的加法。
/* 计算新的聚类中心 */
Node* oldZ = new Node[k]; //保存本次计算前的聚类中心
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
oldZ[i].element[j] = Z[i].element[j];
}
}下图是Add函数的定义
void Add(Node& result, Node X, int n) //矩阵加法
{
for (int i = 0; i < n; i++)
{
result.element[i] = result.element[i] + X.element[i];
}
}判断是否符合迭代结束的条件
接下来是判断是否符合迭代结束的条件。
对比当前迭代计算后得出的聚类中心与上一轮计算后的迭代中心oldZ,若两者相同,则 condition 不变为1,若有一个数据不同则置 condition 为0
/* 判断是否符合迭代结束条件 */
for (int i = 0; i < k; i++)
{
cout << "第" << number << "次迭代计算后聚类中心Z" << i + 1 << "=( ";
for (int j = 0; j < n; j++)
{
cout << Z[i].element[j] << " ";
}
cout << ")\n";
}
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
if (Z[i].element[j] != oldZ[i].element[j])
condition = 0;
}
}判断离开循环,回收内存
最后通过condition来判断是否要离开while循环,然后回收内存
delete[] oldZ;
if (condition == 1)
break;
}
delete[] S;
delete[] N;
delete[] D;
}三、计算过程
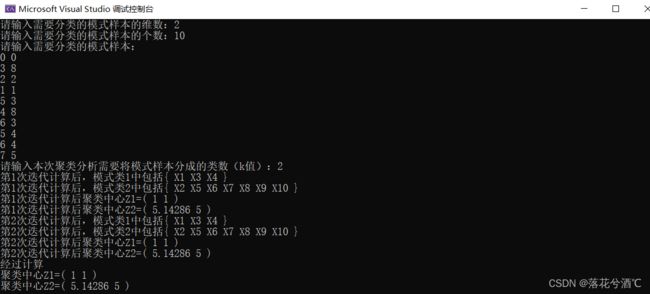
k=2
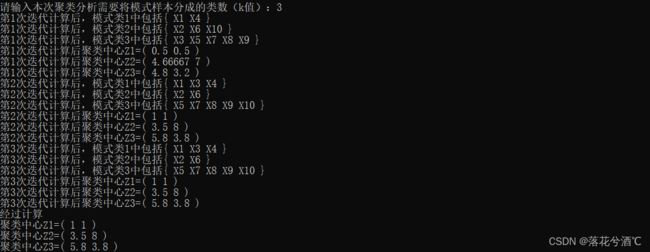
k=3
四、完整代码
/* K-均值算法 */
#include
#include
using namespace std;
#define Number 100 //模式样本的最大维数与个数
struct Node //定义了一个用于存放模式样本的数据结构
{
double element[Number] = { 0 };//模式样本
int kinds = 0; //模式样本所属类别,0为未分类状态
} X[Number];
double Distance(Node X, Node Z, int n) //欧式距离计算函数
{
double result = 0;
for (int i = 0; i < n; i++)
{
result = result + (X.element[i] - Z.element[i]) * (X.element[i] - Z.element[i]);
}
result = sqrt(result);
return result;
}
void Add(Node& result, Node X, int n) //矩阵加法
{
for (int i = 0; i < n; i++)
{
result.element[i] = result.element[i] + X.element[i];
}
}
void Kmeans(int k, Node X[], Node Z[], int m, int n) //K-means算法中迭代计算函数
{
int number = 0; //用于记录迭代计算轮数
double* D = new double[k]; //用于存放迭代计算中距离的变量
int* N = new int[k](); //用于统计每个模式类中的模式样本数
int(*S)[100] = new int[k][100]; //用于统计每个模式类中的模式样本
int condition = 1; //算法结束的条件
while (1) //迭代运算
{
number++;
condition = 1;
for (int i = 0; i < k; i++) //对Ni进行初始化
{
N[i] = 0;
}
/* 分别计算各点与聚类中心的距离 */
for (int i = 0; i < m; i++)
{
for (int j = 0; j < k; j++)
{
D[j] = Distance(X[i], Z[j], n);
}
int temp = 0;
for (int j = 0; j < k; j++)
{
if (D[temp] > D[j])
temp = j;
X[i].kinds = temp + 1;
}
}
/* 统计每个模式类中的样本数和样本 */
for (int i = 0; i < k; i++)
{
cout << "第" << number << "次迭代计算后,模式类" << i + 1 << "中包括{ ";
int temp = 0;
for (int j = 0; j < m; j++)
{
if (X[j].kinds == (i + 1))
{
N[i]++;
S[i][temp] = j;
cout << "X" << S[i][temp] + 1 << " ";
temp++;
}
}
cout << "}\n";
}
/* 计算新的聚类中心 */
Node* oldZ = new Node[k]; //保存本次计算前的聚类中心
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
oldZ[i].element[j] = Z[i].element[j];
}
}
//计算聚类中心
for (int i = 0; i < k; i++)
{
Node result;
for (int j = 0; j < N[i]; j++)
{
Add(result, X[S[i][j]], n);
}
for (int j = 0; j < n; j++)
{
Z[i].element[j] = ((result.element[j]) / N[i]);
}
}
/* 判断是否符合迭代结束条件 */
for (int i = 0; i < k; i++)
{
cout << "第" << number << "次迭代计算后聚类中心Z" << i + 1 << "=( ";
for (int j = 0; j < n; j++)
{
cout << Z[i].element[j] << " ";
}
cout << ")\n";
}
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
if (Z[i].element[j] != oldZ[i].element[j])
condition = 0;
}
}
delete[] oldZ;
if (condition == 1)
break;
}
delete[] S;
delete[] N;
delete[] D;
}
int main()
{
/* 数据的输入与初始化 */
int n; //模式样本的维数
int m; //模式样本的个数
cout << "请输入需要分类的模式样本的维数:";
cin >> n;
cout << "请输入需要分类的模式样本的个数:";
cin >> m;
cout << "请输入需要分类的模式样本:\n";
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
cin >> X[i].element[j];
}
}
int k; //用于K-means算法的k值
while (1)
{
cout << "请输入本次聚类分析需要将模式样本分成的类数(k值):";
cin >> k;
if (k <= 1)
cout << "k值需为大于等于1的整数";
else
break;
}
/* 根据用户输入的k值初始化聚类中心 */
Node* Z = new Node[k]; //聚类中心
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
Z[i].element[j] = X[i].element[j];
}
}
/* 迭代计算聚类中心 */
Kmeans(k,X,Z,m,n);
/* 输出计算结果 */
cout << "经过计算\n";
for (int i = 0; i < k; i++)
{
cout << "聚类中心Z" << i + 1 << "=( ";
for (int j = 0; j < n; j++)
{
cout << Z[i].element[j] << " ";
}
cout << ")\n";
}
delete[] Z;
return 0;
}