机器学习笔记:CNN卷积神经网络
推荐一个网站 CNN Explainer (poloclub.github.io),可以直观地理解CNN的具体过程
1,CNN概述
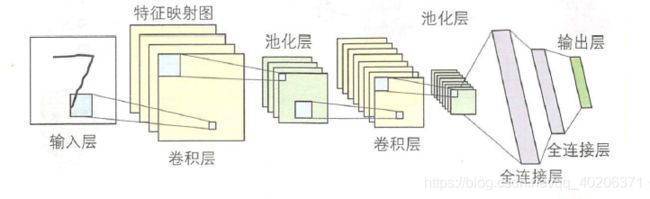
卷积神经网络由输入层、卷积层、池化层、全连接层和输出层组成。
通过增加卷积层和池化层,可以得到更深层次的网络。
与多层感知器相比,卷积神经网络的参数更少,不容易发生过拟合。
2, 为何CNN更适合图像问题
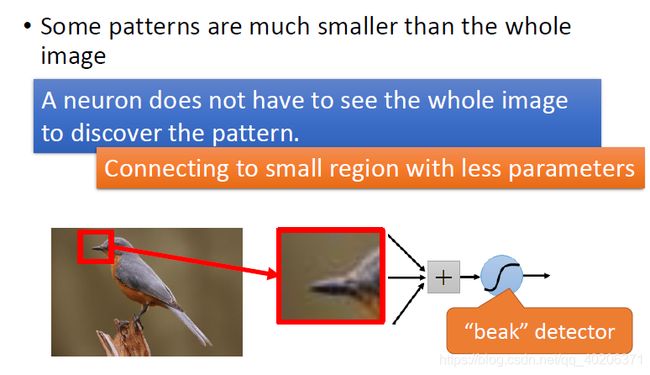
2.1 管中窥豹
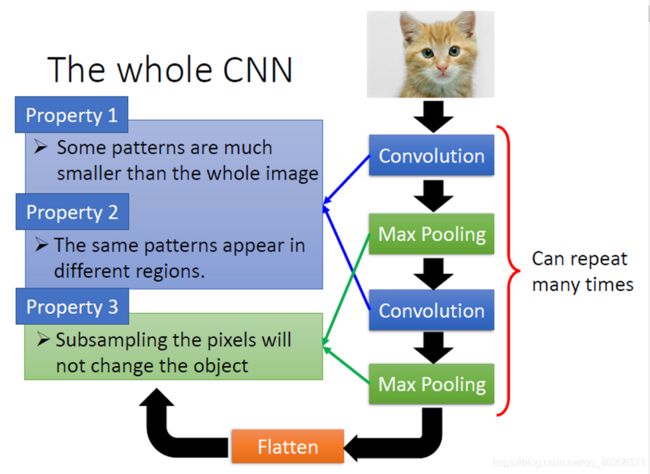
看image的一小部分,就可以识别这个image了,不用看全
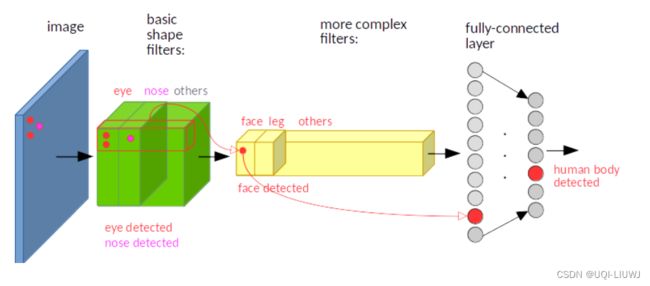
2.2 相同模式(等变性……不变性)
同样的pattern ,出现在image的不同地方,但是这些image表达的是同一个东西
2.2.1 不变性分类
- 平移不变性:Translation Invariance
- 旋转/视角不变性:Ratation/Viewpoint Invariance
- 尺度不变性:Size Invariance
- 光照不变性:Illumination Invariance
2.2.2 平移不变性
- 图像中的目标不管被移动到图片的哪个位置,得到的结果(标签)应该是相同的
- 卷积+最大池化约等于平移不变性
卷积是一种等变性(equivariant)
f(g(x))=g(f(x)) ,f是卷积,g是平移旋转啥的
图像经过平移,相应的特征图上的表达也是平移的。下图只是一个为了说明这个问题的例子。输入图像的左下角有一个人脸,经过卷积,人脸的特征(眼睛,鼻子)也位于特征图的左下角。
假如人脸特征在图像的左上角,那么卷积后对应的特征也在特征图的左上角。但是通过全连接层之后,识别出的特征是不变的
池化可以看成一种近似的不变性
f(x)=f(g(x)),f是池化,g是平移啥的(但如果平移出了感受野,就不是不变性了,所以是近似)
比如最大池化,它返回感受野中的最大值,如果最大值被移动了,但是仍然在这个感受野中,那么池化层也仍然会输出相同的最大值。这就有点平移不变的意思了。
2.3 降采样
进行降采样不会影响image的识别(就是说我行和列都等比例地取一部分)
2.4 CNN的解决之道
3 卷积
3.1 卷积层概述
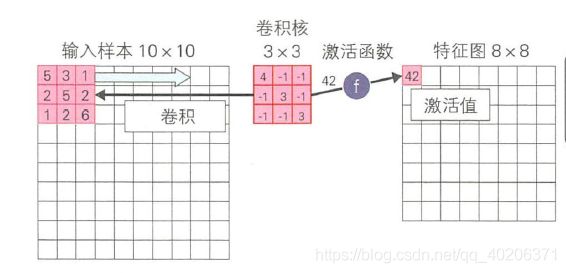
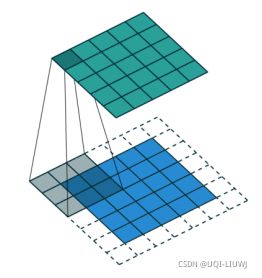
在第一层卷积层对输入样本进行卷积操作后,就可以得到他的特征图(一个卷积层用同一卷积核对每个输入样本进行卷积操作)【一般得到的特征图尺寸小于原图大小】
第二层及之后的卷积层把前一层的特征图作为输入数据,进行卷积操作。(每个位置对应元素乘积之和)
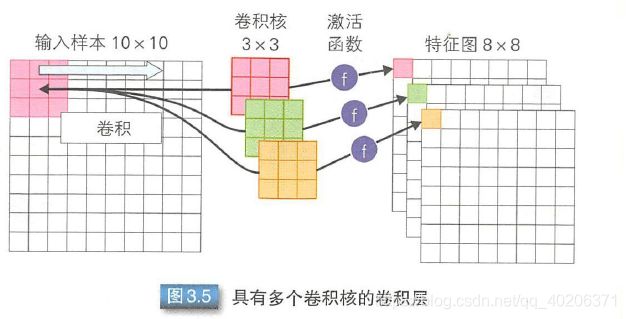
一个卷积层可能有多个卷积核,每个卷积核对应了一个特征图。
共享权值(卷积核)带来的直接好处是减少网络各层之间的连接,同时又降低了过拟合的风险。
filter里面的值是可以被学出来的。某个位置,有几个filter,就会有几个matrix输出。
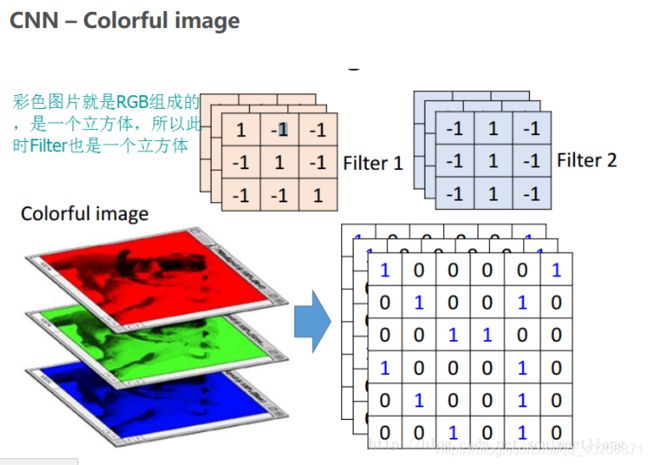
对上图,输入的channel为3,那么卷积层的每一个filter也有3个channel(这里我们filter的维数为3*3*3),每次卷积的时候channel中27个元素和filter中的27个元素做运算。
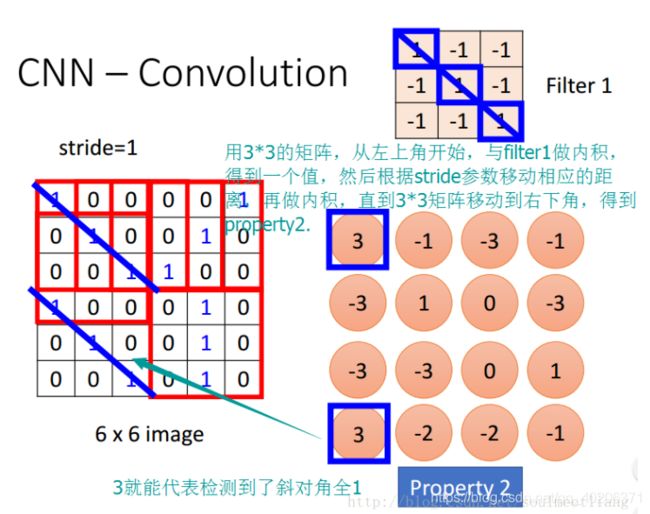
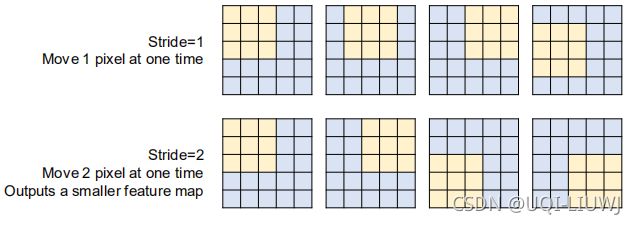
3.2 stride 步长
我们可以手动设置stride步长
stride=1的时候:
n-k表示input中的k*k可以向右移动最多几个,再加上原始的1
3.3 卷积层和全连接神经网络之间的联系
卷积相当于一个连接稀疏的前馈神经网络(基于视野的稀疏,只有此时filter看到的元素可以参与前向传播)——减少参数量
每一个filter作用在每一个filter那么大的input矩阵上,权值是共享的——参数量更少了
3.4 理解in_channel和out_channel之间的联系
以下图的feature_map为例,输入是7*7的图像,其中每个位置不再是一个pixel,而是一个三维向量(即in_channel为3)
为了和in_channel对齐,所以我每一个CNN的filter需要有in_channel(3)个channel(在这里,每一个channel是一个3*3的卷积核 )
输入的这3*3*3个点和卷积核的3*3*3个点相乘,得到输出的一个点的值
输出有out_channel(2)个,每个out_channel需要有一个3*3*3的卷积核
所以一个有in_channel(类似于"行数")*out_channel(类似于"列数")个3*3的卷积核
也就是说,参数个数为in_channel*out_channel*kenel_height*kernel_width
3.4.1 CNN对于参数个数的增益
我们拿MLP做对比:
kernel size:K=3
input_channel:C_in=3
output_channel:C_oout=64
CNN需要的参数个数:K*K*C_in*C_out=1728
对于一张32*32的图像,一个MLP需要 (32*32*3)*(32*32*64)=2,0132,6592个参数!
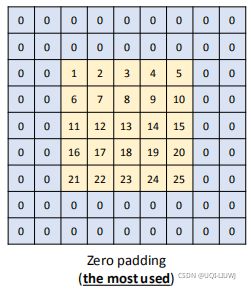
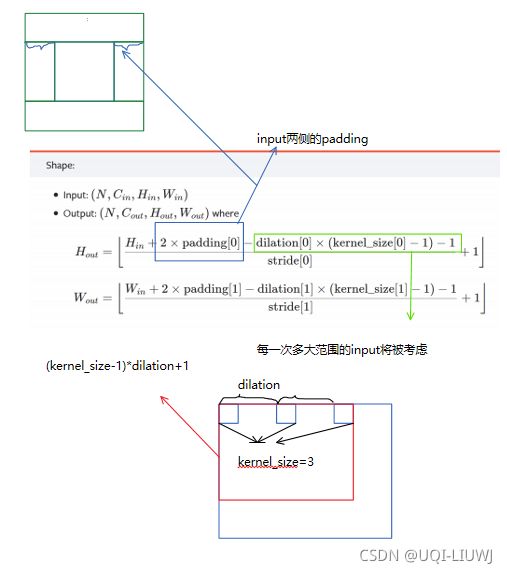
3.5 padding
使用padding,可以让输出和输入尺寸一样
3.5.1 zero-padding
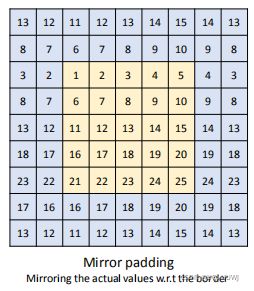
3.5.2 mirror-padding
3.5.3 duplicate padding
用最近的值来填充
3.6 dilation
dilation 的作用是在不增加参数量数量级的情况下,指数级地提升感受野
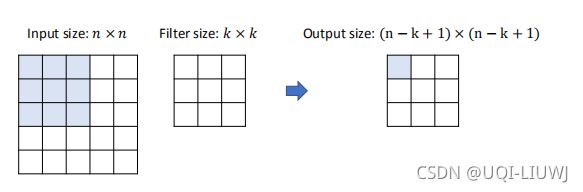
3.7 卷积层输出的大小
3.8 感受野 perceptive field
输出的一个1*1的格子,可以包含输入的k*k的信息
n-k+1=1——>n=k
与此同时,这一个1*1的格子,可以看到上上层(2k-1)*(2k-1)的信息
n-k+1=k——>n=2k-1
上上上层:
n-k+1=2k-1——>n=3k-2
3.8.1 感受野和分辨率
在图像识别问题的神经网络中,很常见的操作是逐渐降低特征图的分辨率。(这个可以由后面的池化操作实现)
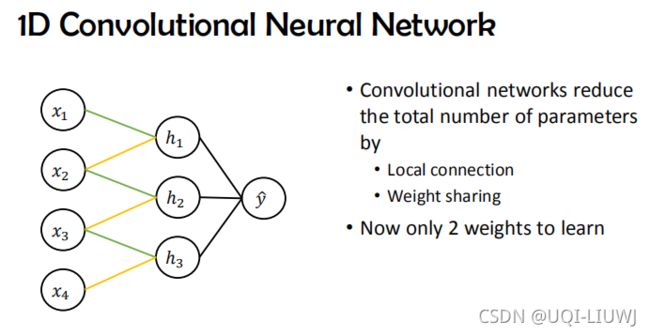
3.9 一维卷积
3.9.1 1*1 卷积
不学习任何空间信息,只是进行channel的整合
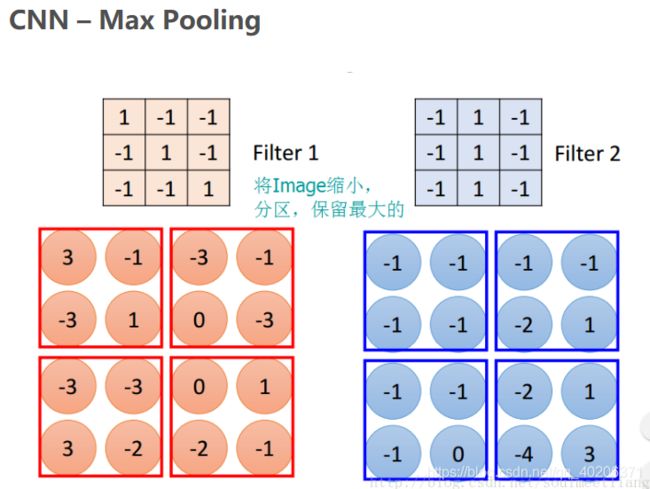
4 池化层
n合一操作
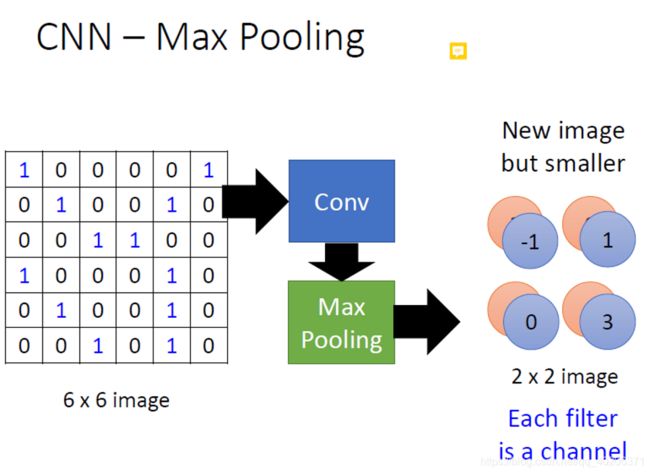
经过卷积层的filter之后的输出:
再经过max-pooling之后的结果:
有不同的池化方式,比较典型的有最大池化、平均池化
参数训练也是采用误差反向传播的方法。误差只会传给池化时选定的单元(类似于前面的卷积,filter没看到的部分是没有连接的,这些元素的信息是不会前向传播到后面的元素的;然后没有被池化层选定的单元连接权重为0,这些元素的信息也是不会前向传播到后面的元素的。所以只有被选中的元素的信息会传递,那么反向传播更新参数的时候也只会把误差传递给这几个元素)
4.1 池化操作的输出大小
和卷积操作一样
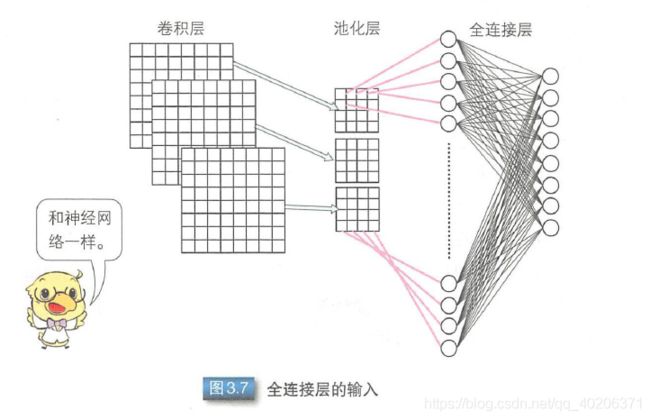
5 flatten+全连接
6 CNN各参数对结果和性能的影响
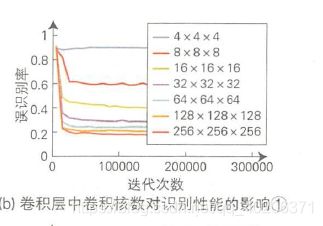
6.1 卷积核大小
卷积核大小——不会对识别性能有很大的影响
6.2 卷积核数量
卷积核越多,识别越好
6.3 激活函数
Relu和maxout好于sigmoid和tanh
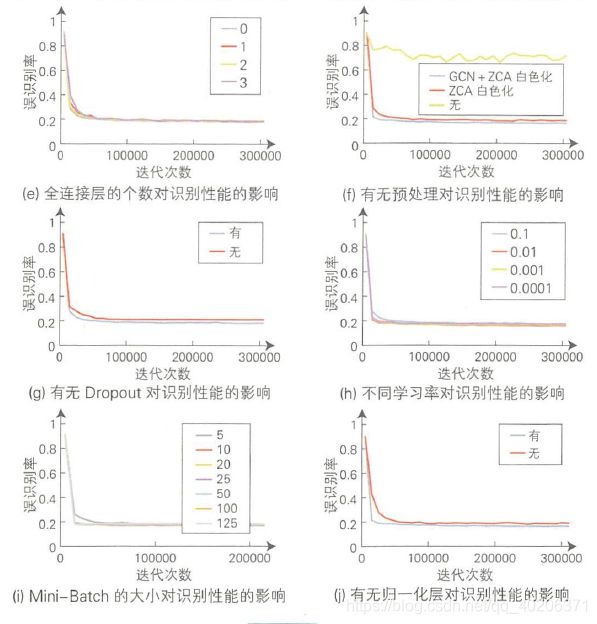
6.4 其他因素的影响
7 CNN应用:deep dream
把CNN一个层上的参数绝对值变大
这样可以让原来的特征被识别得更加“夸张”。
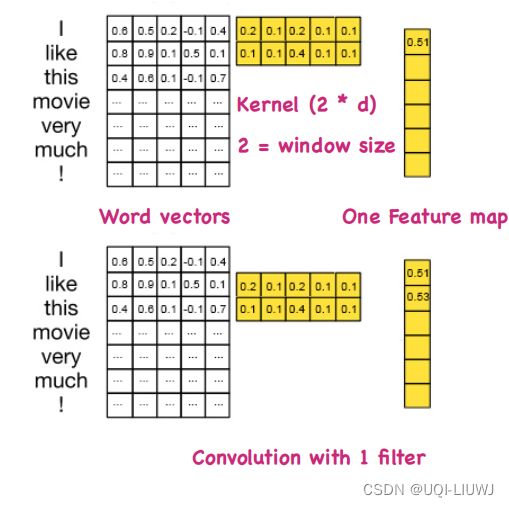
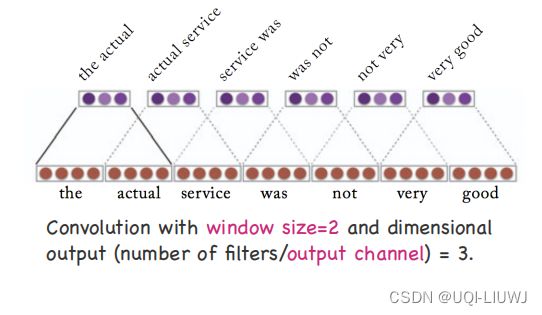
8 CNN用于 NLP问题中
一般都是一维卷积(时间维度)
9 总结
经过一个卷积层之后,image的深度只取决于这个卷积层的filter数目,和之前卷积层中filter的数目无关