机器学习 - 回归 线性回归 Linear Regression(学习笔记)
什么是回归?
“回归”一词最早由英国科学家弗朗西斯·高尔顿提出。1875 年,高尔顿利用子代豌豆与父代豌来确定豌豆尺寸的遗传规律。实验的大意是说:非常矮小的的父辈倾向于有偏高的子代,非常高大的的父辈倾向于有偏矮的子代。这表明子代的身高向着父辈身高的平均值回退,后来人们把这种研究方法称为“回归预测”。
线性回归是什么?
线性回归是预测连续值的问题。基于样本数据拟合出一个可以预测数值的模型,从而实现了回归。利用线性模型来解决“回归问题”,那到底什么是回归问题呢?可以把它理解为“预测”真实值的过程。最简单的线性回归模型是我们所熟知的一次函数(即 y=kx+b),k代表权值参数,b 指的是偏差值。
假设函数
![]()
Y1代表预测结果, X1表示数据样本, b表示用来调整预测结果的“偏差度量值”,而wT表示权值系数的转置。矩阵相乘法是一个求两个向量点积的过程,也就是按位相乘,然后求和 。
损失函数
损失函数的返回值越大就表示预测结果与真实值偏差越大。在线性方程中,要更加复杂、严谨一些,因此我们采用数学中的“均方误差”公式来计算单样本误差:
在机器学习中使用损失函数的目的,是为了使用“优化方法”来求得最小的损失值,这样才能使预测值最逼近真实值。在上述函数中 n、Y、X1 都是已知的,因此只需找到一组 w 与 b 使得上述函数取得最小值即可,这就转变成了数学上二次函数求极值的问题,而这个求极值的过程也就我们所说的“优化方法”。
以上从数学的角度解释了假设函数和损失函数,我们最终的目的要得到一个最佳的“拟合”直线,因此就需要将损失函数的偏差值减到最小,我们把寻找极小值的过程称为“优化方法”,常用的优化方法有很多,比如共轭梯度法、梯度下降法、牛顿法和拟牛顿法。
梯度下降法(Gradient Descent)
如何理解“梯度下降”呢?如果不考虑其他外在因素,可以把它想象成“下山”的场景,如何从一个高山上以最快的时间走到山脚下呢?以所在的当前位置为基准,寻找该位置最陡峭的地方,然后沿着此方向向下走,并且每走一段距离,都要寻找当前位置“最陡峭的地方”,反复采用上述方法,最终就能以最快的时间抵达山脚下。
某个函数在某点的梯度指向该函数取得最大值的方向,那么它的反向自然就是取得最小值的方向。在解决线性回归和逻辑回归问题时,梯度下降方法有着广泛的应用。梯度下降包括批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD),其中批量梯度下降最常用。
sklearn应用线性回归算法
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
#准备自变量x,生成数据集,-3到3的区间均分间隔30份数
x = np.linspace(3,6,40)
#准备因变量y,这一个关于x的假设函数
y=3 * x + 2
# 添加代码,扰乱点的分布
x = x + np.random.rand(40)
#由于fit 需要传入二维矩阵数据,因此需要处理x,y数据格式,将每个样本信息单独作为矩阵的一行
x=[[i] for i in x]
y=[[i] for i in y]
# 构建线性回归模型
model=linear_model.LinearRegression()
# 训练模型,"喂入"数据
model.fit(x,y)
#准备测试数据 x_,这里准备了三组,如下:
x_=[[4],[5],[6]]
# 打印预测结果
y_=model.predict(x_)
print(y_)
#查看拟合准确率情况
print(model.score(x,y))
#查看w和b的
print("w值为:",model.coef_)
print("b截距值为:",model.intercept_)
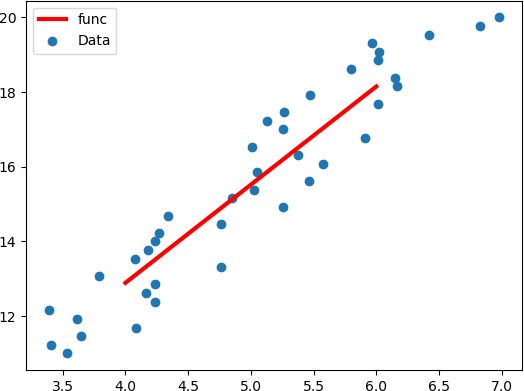
#数据集绘制,散点图,图像满足函假设函数图像
plt.scatter(x,y)
#绘制最佳拟合直线
plt.plot(x_,y_,color="red",linewidth=3.0,linestyle="-")
plt.legend(["func","Data"],loc=0)
plt.show()[[12.88153562] [15.34076249] [17.79998935]] 0.9428561794542006 w值为: [[2.45922686]] b截距值为: [3.04462817]
sklearn包中的线性回归参数分析
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)1.fit_intercept :(截距)默认为True,可选False
2.normalize:(标准化) 默认为True,可选False
3.copy_X:(复制X数据)默认为True,可选False。如果选False会覆盖原数
4.n_jobs:(并行线程数)默认为1,可选int,最大为-1。
总结
线性回归算法简单,且容易理解,但这并不影响它的广泛应用,比如经济金融领域实现股票的预测,以及著名的波士顿房价预测,这些都是线性回归的典型应用。