集成学习Day2 sklearn回归实例 && Day 3 偏差方差理论与测试误差估计 && Day 4模型超参数调优

集成学习Day2 sklearn回归实例 && Day 3 偏差方差理论与测试误差估计 && Day 4模型超参数调优

1. 使用sklearn构建完整机器学习项目的流程

   （1）明确项目任务：回归/分类；
   （2）收集数据集，选择合适的特征；
   （3）选择度量模型性能的指标；
   （4）选择具体的模型并进行训练以优化模型；
   （5）评估模型的性能并调参。

2. 使用sklearn进行Boston房价回归预测

（1）这是一个回归问题

（2）Boston数据集读取与特征分析

from sklearn import datasets 
import pandas as pd 
import numpy as np 

boston = datasets.load_boston()

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 
show_data = boston_data.head()

print(show_data)

数据集各个特征解释：

（3）选择模型度量标准

   a. 均方误差：
$$\text{MSE}\left(y,\hat{y}\right)=\frac{1}{n_{\text{samples}}}\sum _{i=0}^{n_{\text{samples}}}{\left(y_i-{\hat{y}}_i\right)}^2$$
   b. 平均绝对误差：
$$\text{MAE}(y,\hat{y})=\frac{1}{n_{\text{samples}}}\sum _{i=0}^{n_{\text{samples}}}\left|y_i-{\hat{y}}_i\right|$$
   c. $R^2$决定系数：能够由自变量解释的变异程度占总的变异程度的比例
$$R^2(y,\hat{y})=1-\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}$$
   d. 解释方差得分：
$$explained\_variance(y,\hat{y})=1-\frac{Var\{y-\hat{y}\}}{Var\{y\}}$$

   在本例中，选择均方误差MSE作为模型度量标准。

（4）回归模型选择

A. 线性回归的数学模型

   回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（特征）之间的关系。通常用于预测分析、时间序列模型以及发现变量之间的因果关系。通常使用曲线/线来拟合数据点，目标是使曲线到数据点的距离差异最小。而线性回归就是回归问题中的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。通过构建损失函数，来求解损失函数最小时的参数w ：
   假设：数据集$D=\{(x_1,y_1),...,(x_N,y_N)\}$，$x_i\in R^p,y_i\in R,i=1,2,...,N$，$X=(x_1,x_2,...,x_N{)}^T,Y=(y_1,y_2,...,y_N{)}^T$
   假设X和Y之间存在线性关系，模型的具体形式为$\hat{y}=f(w)=w^{T}x$
   a.1 以最小二乘法估计参数$w^T$：衡量真实值$y_i$与线性回归模型的预测值$w^T{x}_i$之间的差距：
$$L(w)=\sum _{i=1}^N||w^T{x}_i-y_i|{|}_2^2=\sum _{i=1}^N(w^T{x}_i-y_i{)}^2=(w^T{X}^T-Y^T)(w^T{X}^T-Y^T{)}^T=w^T{X}^{T}Xw-2w^T{X}^{T}Y+Y{Y}^T$$
为求解参数$w$，采用$\hat{w}=argminL(w)$并求导：
$$\frac{\partial L(w)}{\partial w}=2X^{T}Xw-2X^{T}Y=0$$
因此：$$\hat{w}=(X^{T}X{)}^{-1}{X}^{T}Y$$
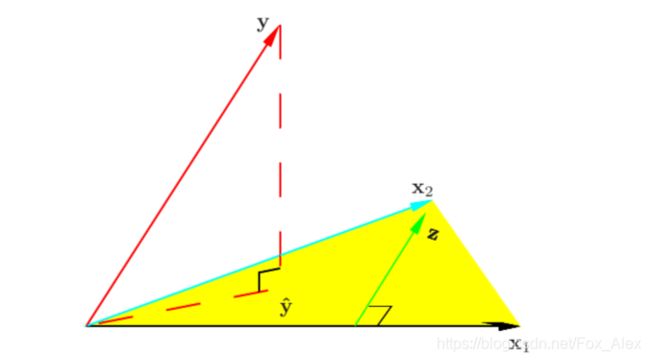
   a.2 几何视角
   平面X的法向量为Y-Xw，与平面X互相垂直，因此：$X^T(Y-Xw)=0$，即：$w=(X^{T}X{)}^{-1}{X}^{T}Y$。

   a.3 概率视角
   假设噪声$ϵ\backsim N(0,{\sigma }^2),y=f(w)+ϵ=w^{T}x+ϵ$，那么使用极大似然估计MLE对参数$w$进行估计：
$$L(w)=logP(Y|X;w)=log\prod _{i=1}^{N}P(y_i|x_i;w)=\sum _{i=1}^{N}logP(y_i|x_i;w)=\sum _{i=1}^{N}log(\frac{1}{\sqrt{2\pi \sigma }}exp(-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}))=\sum _{i=1}^N[log(\frac{1}{\sqrt{2\pi }\sigma })-\frac{1}{2{\sigma }^2}(y_i-w^T{x}_i{)}^2]$$
$$argma{x}_{w}L(w)=argmi{n}_w[l(w)=\sum _{i=1}^N(y_i-w^T{x}_i{)}^2]$$
   因此：线性回归的最小二乘估计$\approx$噪声$ϵ\backsim N(0,{\sigma }^2)$的极大似然估计。

B. 线性回归的sklearn例子

sklearn例子：

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 
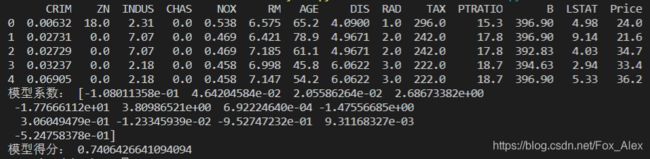
show_data = boston_data.head()

print(show_data)

lin_reg = linear_model.LinearRegression() # create the class of Linear Regression
lin_reg.fit(X, y) # input features X and target Y to train
print("模型系数：", lin_reg.coef_) # output parameters of the model
print("模型得分：", lin_reg.score(X, y)) # output model's R^2

训练结果：

C. 线性回归的推广

  在回归问题中，假设因变量和特征呈线性关系时，线性回归模型是适用的，但当它们之间存在非线性关系时，使用线性回归进行预测的效果就会变得很差，因此需要进行推广。

c.1 多项式回归

  将标准的线性回归模型变为多项式函数：
$$y_i=w_0+w_1{x}_i+w_2{x}_i^2+...+w_d{x}_i^d+ϵ$$
  多项式的阶数一般取3或者4，阶数越大曲线越光滑，但对于边界处对于异常点的波动就会越大，从而导致预测变差。
  sklearn代码：PolynoimalFeatures函数：生成一个新的特征矩阵，由次数小于或等于指定次数的所有特征的多项式组合组成。例如，一个输入样本是二维的，其形式为[a, b]，其二次多项式特征为[1,a, b, a^2, ab, b^2]。

from sklearn.preprocessing import PolynomialFeatures
import numpy as np

X_arr = np.arange(6).reshape(3, 2)
print("原始X为：\n", X_arr)

poly = PolynomialFeatures(2)
print("2次转换X：\n", poly.fit_transform(X_arr))

poly = PolynomialFeatures(interaction_only=True)
print("2次转换X：\n", poly.fit_transform(X_arr))

c.2 广义可加模型GAM

  广义可加模型GAM是线性模型推广到非线性模型的一个框架，在这个框架中每一个变量都用一个非线性函数替换，但模型保持整体可加性。同时GAM还可以将线性分类模型进行推广。
  优点：简单易操作，自然地将线性回归模型推广到非线性，从而提升模型精读。并且由于模型本身是可加的，因此GAM还是能像线性回归模型一样把其他因素控制不变的情况下单独对某个变量进行推断，极大地保留了线性回归的易于推断的性质。
  缺点：GAM模型会经常忽略一些有意义的交互作用，比如某两个特征共同影响因变量，不过GAM还是能像线性回归一样加入交互项$x^{(i)}\times x^{(j)}$ 的形式进行建模；但是GAM模型本质上还是一个可加模型，如果能摆脱可加性模型形式，可能还会提升模型预测精度……
  sklearn代码：

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 
show_data = boston_data.head()

# conda install pygam
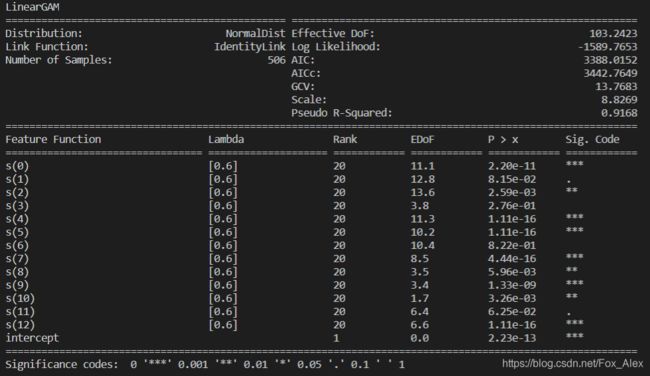
from pygam import LinearGAM

gam = LinearGAM().fit(boston_data[boston.feature_names], y)
gam.summary()

c.3 回归树

   基于树的回归方法是根据分层和分割的方式将特征空间划分为一个个区域，对于某个带预测的自变量，用它所属区域中训练集的平均数或众数对其进行预测，这类方法称为决策树方法。决策树由结点和有向边构成，结点有两种类型：内部结点（表示一个特征或属性）和叶节点（表示一个类别或者某个值），分割后的区域称为叶节点，将特征空间分开的点为内部节点。
   建立回归树的过程大致可以分为以下两步：
   - 将自变量的特征空间(即$x^{(1)},x^{(2)},x^{(3)},...,x^{(p)}$)的可能取值构成的集合分割成J个互不重叠的区域$R_1,R_2,...,R_j$。
   - 对落入区域$R_j$的每个观测值作相同的预测，预测值等于$R_j$上训练集的因变量的简单算术平均。
   具体步骤如下：
   c.3.1 选择最优切分特征j以及该特征上的最优点s：遍历特征j以及固定j后遍历切分点s，选择使得下式最小的(j,s) $$mi{n}_{j,s}[mi{n}_{c_1}\sum _{x_i\in R_1(j,s)}(y_i-c_1{)}^2+mi{n}_{c_2}\sum _{x_i\in R_2(j,s)}(y_i-c_2{)}^2]$$
   c.3.2 按照(j,s)分裂特征空间：$$R_1(j,s)=\{x|x^j\le s\}和R_2(j,s)=\{x|x^j>s\},{\hat{c}}_m=\frac{1}{N_m}\sum _{x\in R_m(j,s)}{y}_i,m=1,2$$
   c.3.3 继续调用步骤a，b直到满足停止条件，就是每个区域的样本数小于等于5。
   c.3.4 将特征空间划分为J个不同的区域，生成回归树：$$f(x)=\sum _{m=1}^J{\hat{c}}_{m}I(x\in R_m)$$
   回归树与线性模型的比较：线性模型的模型形式与树模型的模型形式有着本质的区别，具体而言，线性回归对模型形式做了如下假定：$f(x)=w_0+\sum _{j=1}^p{w}_j{x}^{(j)}$，而回归树则是$f(x)=\sum _{m=1}^J{\hat{c}}_{m}I(x\in R_m)$。那么哪种模型更优呢？这个要视具体情况而言，如果特征变量与因变量的关系能很好的用线性关系来表达，那么线性回归通常有着不错的预测效果，拟合效果则优于不能揭示线性结构的回归树。反之，如果特征变量与因变量的关系呈现高度复杂的非线性，那么树方法比传统方法更优。
   树模型的优缺点：优点：易于理解，可解释性强，可以直接做定性的特征而不需要像线性回归一样哑元化，能很好处理缺失值和异常值，对异常值不敏感，但是这个对线性模型来说却是致命的；缺点：预测准确性不如其他模型，但是可以改进。
   sklearn代码：

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 

from sklearn.tree import DecisionTreeRegressor

reg_tree = DecisionTreeRegressor(criterion="mse", min_samples_leaf=5)
reg_tree.fit(X, y)
print(reg_tree.score(X, y))

   预测得分：

c.4 支持向量回归SVR

   对偶理论详见我之前的博客手推机器学习系列笔记——手推SVM(1)、手推机器学习系列笔记——手推SVM(2)
   在线性回归的理论中，每个样本点都要计算平方损失，但是SVR却是不一样的。SVR认为：落在f(x)的ϵ邻域空间中的样本点不需要计算损失，这些都是预测正确的，其余的落在ϵ邻域空间以外的样本才需要计算损失，因此：
$$\begin{gathered} mi{n}_{w,b,{\xi }_i,{\hat{\xi }}_i}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N({\xi }_i,{\hat{\xi }}_i) \\ s.t.f(x_i)-y_i\le ϵ+{\xi }_i \\ {y}_i-f(x_i)\le ϵ+{\hat{\xi }}_i \\ {\xi }_i,{\hat{\xi }}_i\le 0,i=1,2,...,N \end{gathered}$$
  引入拉格朗日函数：
$$\begin{array}{l}L(w,b,\alpha ,\hat{\alpha },\xi ,\xi ,\mu ,\hat{\mu })\\ =\frac{1}{2}\Vert w{\Vert }^2+C{\sum }_{i=1}^N\left({\xi }_i+{\xi }_i\right)-{\sum }_{i=1}^N{\xi }_i{\mu }_i-{\sum }_{i=1}^N{\xi }_i{\mu }_i\\ +{\sum }_{i=1}^N{\alpha }_i\left(f\left(x_i\right)-y_i-ϵ-{\xi }_i\right)+{\sum }_{i=1}^N{\alpha }_i\left(y_i-f\left(x_i\right)-ϵ-{\xi }_i\right)\end{array}$$
  再令$L(w,b,\alpha ,\hat{\alpha },\xi ,\xi ,\mu ,\hat{\mu })$对$w,b,\xi ,\hat{\xi }$求偏导等于0，得： $w={\sum }_{i=1}^N\left({\alpha }_i-{\alpha }_i\right)x_i$。
上述过程中需满足KKT条件，即要求：
$$\{\begin{array}{c}{\alpha }_i\left(f\left(x_i\right)-y_i-ϵ-{\xi }_i\right)=0\\ \widehat{{\alpha }_i}\left(y_i-f\left(x_i\right)-ϵ-{\hat{\xi }}_i\right)=0\\ {\alpha }_i{\alpha }_i=0,{\xi }_i{\hat{\xi }}_i=0\\ \left(C-{\alpha }_i\right){\xi }_i=0,\left(C-{\alpha }_i\right){\hat{\xi }}_i=0\end{array}$$
  SVR的解形如:$f(x)={\sum }_{i=1}^N\left({\alpha }_i-{\alpha }_i\right)x_i^{T}x+b$

   sklearn代码：

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 

from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler # 标准化数据
from sklearn.pipeline import make_pipeline # 使用管道，将预处理和模型变为一个流程

reg_svr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
reg_svr.fit(X, y)
print(reg_svr.score(X, y))

函数原型：sklearn.svm.SVR(*, kernel=‘rbf’, degree=3, gamma=‘scale’, coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)
参数：
kernel：核函数，{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, 默认=’rbf’ 径向基；
degree：多项式核函数的阶数。默认 = 3；
C：正则化参数，默认=1.0；
epsilon：SVR模型允许的不计算误差的邻域大小，默认0.1。

（5）模型优化

A 过拟合与欠拟合

   在回归问题中，我们最常用用均方误差来进行评价，即：$MSE=\frac{1}{N}\sum _{i=1}^N(y_i-\hat{f}(x_i){)}^2$，其中$\hat{f}(x_i)$是样本$x_i$应用建立的模型$\hat{f}$预测的结果通常我们的模型在训练集上进行训练，来最小化训练均方误差，但是真正目的在于希望模型能在测试集取得好的表现（即具有小的测试均方误差），训练均方误差和测试均方误差没有直接的关系，一般地我们认为训练均方误差越小那么模型在测试集上的测试均方误差越小，但会出现模型在训练集上的训练均方误差很小而在测试集上的测试均方误差很大，称为过拟合；欠拟合即模型在训练集上的训练均方误差就很大。

B 偏差-方差分解理论

从下图的测试误差曲线图中可以看出，红色线呈现出“U”型变化：

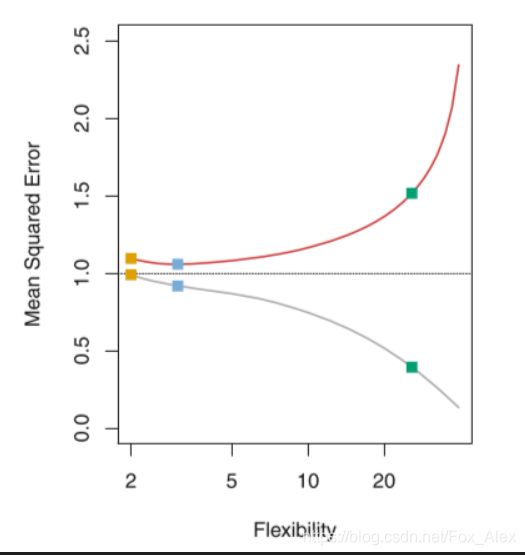
   则下列公式可被证明：
$$E{\left(y_0-\hat{f}\left(x_0\right)\right)}^2=\mathrm{Var}\left(\hat{f}\left(x_0\right)\right)+{\left[\mathrm{Bias}\left(\hat{f}\left(x_0\right)\right)\right]}^2+\mathrm{Var}(\epsilon )$$
   我们可以将测试均方误差的期望值可以分解为$\hat{f}(x_0)$的方差、$\hat{f}(x_0)$的偏差平方以及误差项$ϵ$的方差。为了使模型的测试均方误差最小，即最小化偏差平方以及方差，但偏差平方和方差都是非负的，因此测试均方误差的期望不低于误差的方差，将$\mathrm{Var}(\epsilon )$称为建模任务的难度，这个量在问题确定后就不可更改，也叫不可约误差。而模型的方差就是用不同数据集来估计$f$时，估计函数的改变量，一般来说模型复杂度越高，$f$的方差就越大；模型的偏差指的是：为了选择一个简单的模型去古巨基真实函数所带入的误差，例如真实的函数是X和Y的二次关系，却使用线性模型来建模，那这种由模型复杂度引起的误差成为偏差。偏差衡量的是算法的期望预测和真实结果的偏离程度，即刻画了学习算法本身的拟合能力（模型的学能力），而方差度量的是模型在不同数据集上的稳定性。
  偏差-方差分解说明：泛化性是由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定的，给定一个学习任务，为了获得好的泛化性，则需要使偏差更小（更加充分的拟合数据）并且使方差更小（使数据扰动产生的影响小）。

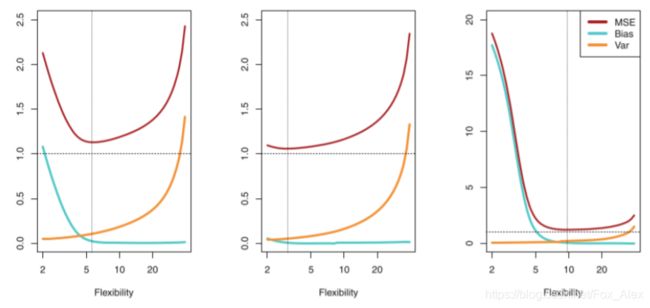
C 测试估计误差

  要想选择一个测试误差得到最小的模型，但实际上很难对训练误差进行精确的计算，我们就需要对测试误差进行估计，估计的方法有两种：训练误差修正和交叉验证。
  C.1 训练误差修正
  模型越复杂，它的训练误差会减小，但同时测试误差会先减少后增加。因此，可以先构造一个特征较多的模型使其过拟合，这个时候训练误差很小但测试误差较大，然后加入关于特征个数的罚项，因此当训练误差随特征个数的增加而减少时，罚项因为特征数量的增加而增加，抑制了训练误差随特征个数的增加而无休止的减少。$C_p=\frac{1}{N}(RSS+2d{\hat{\sigma }}^2)$，其中d为模型特征个数，$RSS=\sum _{i=1}^N(y_i-\hat{f}(x_i){)}^2$，${\hat{\sigma }}^2$为模型预测误差的方差的估计值，即残差的方差。
  AIC赤池信息量准则：$AIC=\frac{1}{d{\hat{\sigma }}^2}(RSS+2d{\hat{\sigma }}^2)$
  BIC贝叶斯信息量准则：$BIC=\frac{1}{n}(RSS+log(n)d{\hat{\sigma }}^2)$
  C.2 交叉验证
  前面对训练误差修正得到测试误差的估计是间接方法，而交叉验证则是对测试误差的直接估计。交叉验证相比训练误差修正的优势在于：能够给出测试误差的一个直接估计。常用的K折交叉验证：我们把训练样本分成K等分，然后用K-1个样本集当做训练集，剩下的一份样本集为验证集去估计由K-1个样本集得到的模型的精度，这个过程重复K次取平均值得到测试误差的一个估计$C{V}_{(K)}=\frac{1}{K}\sum _{i=1}^{K}MS{E}_i$。

D 特征选择

  在测试误差能够被合理的估计出来以后，我们做特征选择的目标就是：从p个特征中选择m个特征，使得对应的模型的测试误差的估计最小。对应的方法有：
  - 最优子集选择：
    (i) 记不含任何特征的模型为$M_0$，计算这个$M_0$的测试误差；
    (ii) 在$M_0$基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作$M_1$，并计算该模型$M_1$的测试误差；
    (iii) 再增加变量，计算p-1个模型的RSS，并选择RSS最小的模型记作$M_2$，并计算该模型$M_2$的测试误差；
    (iv) 重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型$\{M_0,M_1,...,M_p\}$中测试误差最小的模型作为最优模型。
  - 向前逐步选择：
  最优子集选择虽然在原理上很直观，但是随着数据特征维度p的增加，子集的数量为$2^p$，计算效率非常低下且需要的计算内存也很高，在大数据的背景下显然不适用。因此，我们需要把最优子集选择的运算效率提高，因此向前逐步选择算法的过程如下：
    (i) 记不含任何特征的模型为$M_0$，计算这个$M_0$的测试误差；
    (ii) 在$M_0$基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作$M_1$，并计算该模型$M_1$的测试误差；
    (iii) 在最小的RSS模型下继续增加一个变量，选择RSS最小的模型记作$M_2$，并计算该模型$M_2$的测试误差；
    (iv) 以此类推，重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型$\{M_0,M_1,...,M_p\}$中测试误差最小的模型作为最优模型。

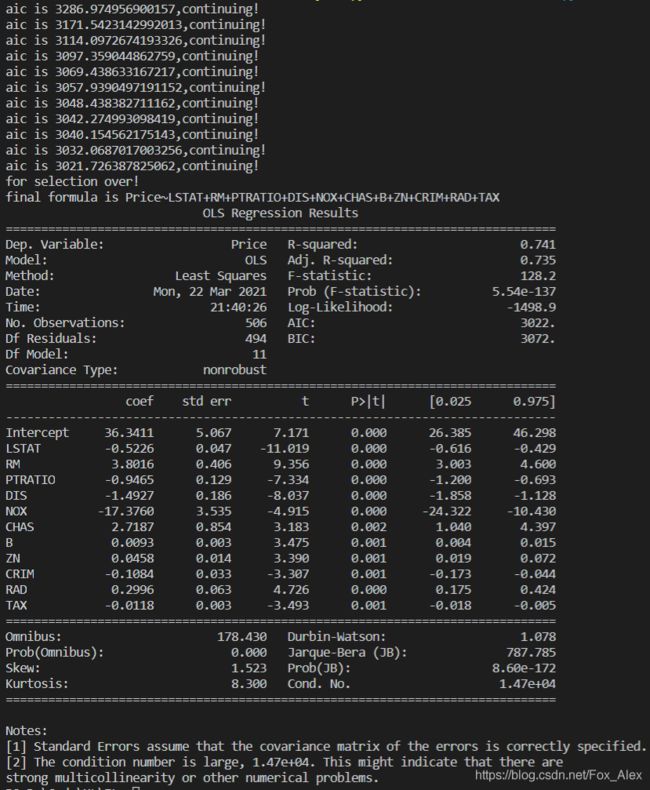
  特征提取实例：根据AIC准则定义向前逐步回归进行变量筛选

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

import statsmodels.api as sm # 最小二乘
from statsmodels.formula.api import ols # 加载ols模型

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 
show_data = boston_data.head()


# 定义向前逐步回归函数
def forward_select(data,target):
    variate=set(data.columns)  # 将字段名转换成字典类型
    variate.remove(target)  # 去掉因变量的字段名
    selected=[]
    current_score,best_new_score=float('inf'),float('inf')  # 目前的分数和最好分数初始值都为无穷大（因为AIC越小越好）
    # 循环筛选变量
    while variate:
        aic_with_variate=[]
        for candidate in variate:  # 逐个遍历自变量
            formula="{}~{}".format(target,"+".join(selected+[candidate]))  # 将自变量名连接起来
            aic=ols(formula=formula,data=data).fit().aic  # 利用ols训练模型得出aic值
            aic_with_variate.append((aic,candidate))  # 将第每一次的aic值放进空列表
        aic_with_variate.sort(reverse=True)  # 降序排序aic值
        best_new_score,best_candidate=aic_with_variate.pop()  # 最好的aic值等于删除列表的最后一个值，以及最好的自变量等于列表最后一个自变量
        if current_score>best_new_score:  # 如果目前的aic值大于最好的aic值
            variate.remove(best_candidate)  # 移除加进来的变量名，即第二次循环时，不考虑此自变量了
            selected.append(best_candidate)  # 将此自变量作为加进模型中的自变量
            current_score=best_new_score  # 最新的分数等于最好的分数
            print("aic is {},continuing!".format(current_score))  # 输出最小的aic值
        else:
            print("for selection over!")
            break
    formula="{}~{}".format(target,"+".join(selected))  # 最终的模型式子
    print("final formula is {}".format(formula))
    model=ols(formula=formula,data=data).fit()
    return(model)

forward_select(data=boston_data,target="Price")
lm=ols("Price~LSTAT+RM+PTRATIO+DIS+NOX+CHAS+B+ZN+CRIM+RAD+TAX",data=boston_data).fit()
print(lm.summary())

E 压缩估计（正则化）

  除了刚刚讨论的直接对特征自身进行选择以外，我们还可以对回归的系数进行约束或者加罚的技巧对p个特征的模型进行拟合，显著降低模型方差，这样也会提高模型的拟合效果。具体来说，就是将回归系数往零的方向压缩，这也就是为什么叫压缩估计的原因了。
  E.1 岭回归(L2正则化的例子)：
  在线性回归中，我们的损失函数为$J(w)=\sum _{i=1}^N(y_i-w_0-\sum _{j=1}^p{w}_j{x}_{ij}{)}^2$，我们在线性回归的损失函数的基础上添加对系数的约束或者惩罚，即：
$$\begin{gathered} J(w)=\sum _{i=1}^N(y_i-w_0-\sum _{j=1}^p{w}_j{x}_{ij}{)}^2+\lambda \sum _{j=1}^p{w}_j^2,其中，\lambda \ge 0 \\ \hat{w}=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y \end{gathered}$$
  调节参数$\lambda$的大小是影响压缩估计的关键，$\lambda$越大，惩罚的力度越大，系数则越趋近于0，反之，选择合适的$\lambda$对模型精度来说十分重要。岭回归通过牺牲线性回归的无偏性降低方差，有可能使得模型整体的测试误差较小，提高模型的泛化能力。
  岭回归实例

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 
reg_rid = linear_model.Ridge(alpha=.5)
reg_rid.fit(X,y)
print(reg_rid.score(X,y))

  E.2 Lasso回归(L1正则化的例子)：
  岭回归的一个很显著的特点是：将模型的系数往零的方向压缩，但是岭回归的系数只能呢个趋于0但无法等于0，换句话说，就是无法做特征选择。能否使用压缩估计的思想做到像特征最优子集选择那样提取出重要的特征呢？答案是肯定的！我们只需要对岭回归的优化函数做小小的调整就行了，我们使用系数向量的L1范数替换岭回归中的L2范数：
$$J(w)=\sum _{i=1}^N(y_i-w_0-\sum _{j=1}^p{w}_j{x}_{ij}{)}^2+\lambda \sum _{j=1}^p|w_j|,其中，\lambda \ge 0$$
  为什么Losso能做到特征选择而岭回归却不能呢个做到呢？(如图：左边为lasso，右边为岭回归)

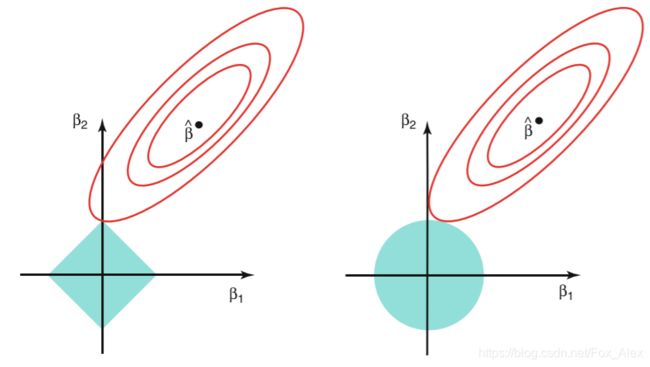
  椭圆形曲线为RSS等高线，菱形和圆形区域分别代表了L1和L2约束，Lsaao回归和岭回归都是在约束下的回归，因此最优的参数为椭圆形曲线与菱形和圆形区域相切的点。但是Lasso回归的约束在每个坐标轴上都有拐角，因此当RSS曲线与坐标轴相交时恰好回归系数中的某一个为0，这样就实现了特征提取。反观岭回归的约束是一个圆域，没有尖点，因此与RSS曲线相交的地方一般不会出现在坐标轴上，因此无法让某个特征的系数为0，因此无法做到特征提取。

  Lasso实例

from sklearn import datasets 
from sklearn import linear_model
import pandas as pd 
import numpy as np 

boston = datasets.load_boston() # load boston dataset

X = boston.data 
y = boston.target  
features = boston.feature_names 
boston_data = pd.DataFrame(X, columns=features)
boston_data["Price"] = y 
# reg_rid = linear_model.Ridge(alpha=.5)
# reg_rid.fit(X,y)
# print(reg_rid.score(X,y))


reg_lasso = linear_model.Lasso(alpha=0.5)
reg_lasso.fit(X,y)
print(reg_lasso.score(X,y))

F 降维

  到目前为止，我们所讨论的方法对方差的控制有两种方式：一种是使用原始变量的子集，另一种是将变量系数压缩至零。但是这些方法都是基于原始特征$x_1,...,x_p$得到的，现在我们探讨一类新的方法：将原始的特征空间投影到一个低维的空间实现变量的数量变少，如：将二维的平面投影至一维空间。机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们希望减少 冗余信息 所造成的误差,提高识别（或其他应用）的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。在很多算法中，降维算法成为了数据预处理的一部分，如PCA。事实上，有一些算法如果没有降维预处理，其实是很难得到很好的效果的。
  主成分分析(PCA)：
  主成分分析的思想：通过最大投影方差 将原始空间进行重构，即由特征相关重构为无关，即落在某个方向上的点(投影)的方差最大。在进行下一步推导之前，我们先把样本均值和样本协方差矩阵推广至矩阵形式：
  样本均值Mean:$\bar{x}=\frac{1}{N}\sum _{i=1}^N{x}_i=\frac{1}{N}{X}^T{1}_N,其中1_N=(1,1,...,1{)}_N^T$
  样本协方差矩阵$S^2=\frac{1}{N}\sum _{i=1}^N(x_i-\bar{x})(x_i-\bar{x}{)}^T=\frac{1}{N}{X}^{T}HX,其中，H=I_N-\frac{1}{N}{1}_N{1}_N^T$
  最大投影方差的步骤：
  (i) 中心化：$x_i-\bar{x}$
  (ii) 计算每个点$x_1,...,x_N$至$u_1$方向上的投影：$(x_i-\bar{x})u_1,||u_1||=1$
  (iii) 计算投影方差：$J=\frac{1}{N}\sum _{i=1}^N[(x_i-\bar{x}{)}^T{u}_1{]}^2,||u_1||=1$
  (iv) 最大化投影方差求$u_1$：
$$\begin{gathered} {\bar{u}}_1=argma{x}_{u_1}\frac{1}{N}\sum _{i=1}^N[(x_i-\bar{x}{)}^T{u}_1{]}^2 \\ s.t.u_1^T{u}_1=1(u_1往后不带向量符号) \end{gathered}$$
    得到：
$$\begin{gathered} J=\frac{1}{N}\sum _{i=1}^N[(x_i-\bar{x}{)}^T{u}_1{]}^2=\frac{1}{N}\sum _{i=1}^N[u_1^T(x_i-\bar{x})(x_i-\bar{x}{)}^T{u}_1] \\ =u_1^T[\frac{1}{N}\sum _{i=1}^N(x_i-\bar{x})(x_i-\bar{x}{)}^T]u_1=u_1^T{S}^2{u}_1 \end{gathered}$$
     即：
$$\begin{gathered} {\hat{u}}_1=argma{x}_{u_1}{u}_1^T{S}^2{u}_1,s.t.u_1^T{u}_1=1 \\ L(u_1,\lambda )=u_1^T{S}^2{u}_1+\lambda (1-u_1^T{u}_1) \\ \frac{\partial L}{\partial u_1}=2S^2{u}_1-2\lambda u_1=0 \\ 即：S^2{u}_1=\lambda u_1 \end{gathered}$$
  可以看到：$\lambda$为$S^2$的特征值，$u_1$为$S^2$的特征向量。因此我们只需要对中心化后的协方差矩阵进行特征值分解，得到的特征向量即为投影方向。如果需要进行降维，那么只需要取p的前M个特征向量即可。

（6）超参数调优

A 模型参数与超参数

  模型参数与超参数有着很大的差别。参数（模型参数）是模型内部的配置变量，其值以从数据中估计等方式获得，定义了可使用的模型，不需要手动设置；超参数（模型超参数）通常用于帮助估计模型参数，通常是由人工指定的，也可以使用启发式的设置。

B 网格搜索sklearn例子

  上述（5）中提的优化方法是从模型算法本身的改进的，例如在线性回归中使用岭回归进行优化——在线性回归的损失函数中加入L2正则项从而降低方差但同时也牺牲了无偏性。但对于这个问题，L2正则化的超参数$\lambda$应该取多少，这属于最优化的内容，可以使用网格搜索方法进行超参数的确定。
  网格搜索：比如有2个超参数需要选择，那么把所有超参数的可能取值列出来然后做排列组合。举个例子：$\lambda =0.01,0.1,1.0$和$\alpha =0.01,0.1,1.0$，你可以做一个排列组合，即：{[0.01,0.01],[0.01,0.1]，[0.01,1]，[0.1,0.01]，[0.1,0.1]，[0.1,1.0]，[1,0.01]，[1,0.1]，[1,1]} ，然后针对每组超参数分别建立一个模型，最后选择测试误差最小的那组超参数。换句话说，我们需要从超参数空间中寻找最优的超参数，很像一个网格中找到一个最优的节点，因此叫网格搜索。

from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline # make pipeline
from sklearn.preprocessing import StandardScaler # standard processing
from sklearn.model_selection import GridSearchCV # search grid
from sklearn.model_selection import cross_val_score # k-cross 
from sklearn.pipeline import Pipeline
from sklearn.model_selection import RandomizedSearchCV
from sklearn import datasets
import numpy as np

from scipy.stats import uniform

boston = datasets.load_boston()
X = boston.data  
y = boston.target 
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(), SVR())

score1 = cross_val_score(estimator=pipe_SVR, X=X, y=y, scoring='r2', cv=10) # 10 times
print("CV accuracy: %.3f +/- %.3f" % ((np.mean(score1)),np.std(score1)))

pipe_svr = Pipeline([("StandardScaler",StandardScaler()), ("svr",SVR())])
param_range = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]
param_grid = [{"svr__C":param_range, "svr__kernel":["linear"]},   # 注意__是指两个下划线，一个下划线会报错的
               {"svr__C":param_range, "svr__gamma":param_range, "svr__kernel":["rbf"]}]
gs = GridSearchCV(estimator=pipe_svr, param_grid=param_grid, scoring='r2', cv=10)
gs = gs.fit(X, y)

print("网格搜索最优得分：",gs.best_score_)
print("网格搜索最优参数组合：\n",gs.best_params_)

C 随机搜索sklearn例子

  相当于暴力尝试参数空间的每一种组合，然后选择最优的那组参数，这样的方法随着参数个数的增加，尝试的次数也呈现指数级增加，这样显然是非常低效的。随机搜索方法是一种补充方法，实验验证了随机搜索方法在一些情况下效率很高。参数的随机搜索中每个参数都是从可能的参数的分布中采样的，相比于网格搜索，它可以独立于参数数量和可能的取值来选择计算成本，并且添加不影响性能的参数不会降低效率。

from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline # make pipeline
from sklearn.preprocessing import StandardScaler # standard processing
from sklearn.model_selection import GridSearchCV # search grid
from sklearn.model_selection import cross_val_score # k-cross 
from sklearn.pipeline import Pipeline
from sklearn.model_selection import RandomizedSearchCV
from sklearn import datasets
import numpy as np

from scipy.stats import uniform

boston = datasets.load_boston()
X = boston.data  
y = boston.target 
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(), SVR())

score1 = cross_val_score(estimator=pipe_SVR, X=X, y=y, scoring='r2', cv=10) # 10 times
print("CV accuracy: %.3f +/- %.3f" % ((np.mean(score1)),np.std(score1)))

pipe_svr = Pipeline([("StandardScaler", StandardScaler()), ("svr", SVR())])
distributions = dict(svr__C=uniform(loc=1.0, scale=4), svr__kernel=["linear", "rbf"], svr__gamma=uniform(loc=0, scale=4)) # 两个__
rs = RandomizedSearchCV(estimator=pipe_svr, param_distributions=distributions, scoring='r2', cv=10)
rs = rs.fit(X, y)
print("随机搜索最优得分：",rs.best_score_)
print("随机搜索最优参数组合：\n",rs.best_params_)

  随机搜索的速度是非常快的，每次的结果也是不相同的。其准确率有待继续研究。

参考：
1. DataWhale组对学习-集成学习
2. sklearn官方文档：PolynomialFeatures函数
3. sklearn官方文档：SVR函数
4. sklearn官方文档：网格搜索GridSearchCV
5. sklearn官方文档：网格搜索结合管道GridSearchCV+Pipeline