k均值聚类算法案例 r语言iris_大数据小白入门——KMeans聚类算法

导读

K-Means聚类算法也称k均值聚类算法,是集简单和经典于一身的基于距离的聚类算法。它采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。K-Means聚类算法作为基于划分聚类算法的一个典型算法,在数据挖掘中被广泛应用,经常被用来作为预处理步骤。本章实验还是以鸢尾花数据为例,进行K-Means聚类算法的实现。
数据下载地址:https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data

算法核心思想

K-means聚类算法是一种迭代求解的聚类分析算法,其步骤是随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。

算法步骤图解


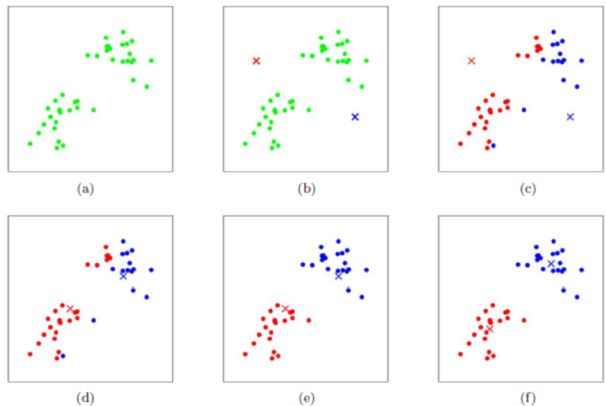
上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图d所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。

TF-IDF算法实现过程
 第一步,导入实验要用到的包工具
第一步,导入实验要用到的包工具
import org.apache.spark.ml.clustering.{KMeans,KMeansModel}import org.apache.spark.ml.linalg.Vectorsimport org.apache.spark.sql.SparkSession引入spark.implicits._,以便于RDDs和DataFrames之间的隐式转换
import spark.implicits._
第二步,定义一个case class作为DataFrame每一个数据样本的数据类型。case class model_examples (features: org.apache.spark.ml.linalg.Vector)第三步,把定义完成的数据读入RDD结构中去,并通过RDD的隐式转换.toDF()方法完成RDD到DataFrame的转换(实验数据还是采用的):
val rawData = sc.textFile("file:///data/iris.data")val df = rawData.map(line =>{ model_examples( Vectors.dense(line.split(",").filter(p => p.matches("\\d*(\\.?)\\d*")).map(_.toDouble)) )}).toDF()val kmeansmodel = new KMeans().setK(3).setFeaturesCol("features").setPredictionCol("prediction").fit(df)第五步,使用transform()方法将存储在DataFrame中的给定数据集进行整体处理,生成带有预测簇标签的数据集
val results = kmeansmodel.transform(df)
第六步,使用collect()方法,该方法将DataFrame中所有的数据组织成一个Array对象进行返回
results.collect().foreach(row => { println( row(0) + " is predicted as cluster " + row(1)) })第七步,使用kmeansmodel类中自带的clusterCenters属性查看iris数据中所有类别的聚类中心情况
kmeansmodel.clusterCenters.foreach( center => { println("Clustering Center:"+center) })最后对K-Means聚类算法进行总结,主要经过以下四步实现算法操作:
1、确定一个k值,即我们希望将数据集经过聚类得到k个集合。
2、从数据集中随机选择k个数据点作为质心。
3、对数据集中每一个点,计算其与每一个质心的距离(如欧式距离),离哪个质心近,就划分到那个质心所属的集合。
4、把所有数据归好集合后,得到k个集合,最后重新计算每个集合的质心。
 扫码关注小白白AI学习
扫码关注小白白AI学习