【数据挖掘】心跳信号分类预测 之 赛题理解 —— 学习笔记（一）

---

一、赛题理解

本赛是 Datawhale 与天池联合发起的零基础入门系列赛事第五场 —— 零基础入门心电图心跳信号多分类预测挑战赛。

2016 年 6 月，国务院办公厅印发《国务院办公厅关于促进和规范健康医疗大数据应用发展的指导意见》,文件指出健康医疗大数据应用发展将带来健康医疗模式的深刻变化，有利于提升健康医疗服务效率和质量。

赛题以心电图数据为背景，要求选手根据心电图感应数据预测心跳信号，其中心跳信号对应正常病例以及受不同心律不齐和心肌梗塞影响的病例，这是一个多分类的问题。通过这道赛题来引导大家了解医疗大数据的应用，帮助竞赛新人进行自我练习、自我提高。

比赛地址与赛题细节：天池-心跳信号分类预测

1.1 学习目标

• 理解赛题数据和目标，清楚评分体系
• 完成报名，下载数据，提交打卡，熟悉比赛流程

1.2 了解赛题

• 赛题概况
• 数据概况
• 预测指标
• 分析赛题

1.2.1 赛题概况

比赛要求参赛选手根据给定的数据集，建立模型，预测不同的心跳信号。赛题以预测心电图心跳信号类别为任务，数据集报名后可见并可下载，该该数据来自某平台心电图数据记录，总数据量超过 20 万，主要为 1 列心跳信号序列数据，其中每个样本的信号序列采样频次一致，长度相等。为保证比赛的公平性，将从中抽取 10 万条作为训练集，2 万条作为测试集 A，2 万条作为测试集 B，同时会对心跳信号类别 (label) 信息进行脱敏。

通过这道赛题来引导大家走进医疗大数据的世界，主要针对于于竞赛新人进行自我练习，自我提高。

1.2.2 数据概况

一般而言，对于数据在比赛界面都有对应的数据概况介绍 (匿名特征除外)，说明列的性质特征。了解列的性质会有助于对数据的理解和后续分析。其中， 匿名特征 即未告知数据列所属的性质的特征列。

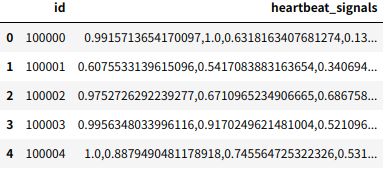
文件 train.csv 包含特征：

• id 为心跳信号分配的唯一标识
• heartbeat_signals 为心跳信号序列(数据之间采用“,”进行分隔)
• label 为心跳信号类别 (0、1、2、3)

文件 testA.csv 包含特征：

• id 心跳信号分配的唯一标识
• heartbeat_signals 心跳信号序列(数据之间采用“,”进行分隔)

1.2.3 预测指标

选手需提交 4 种不同心跳信号预测的概率，提交结果与实际心跳类型结果进行对比，求预测的概率与真实值差值的绝对值。

具体计算公式如下：

设，总共有 $n$ 个病例，针对某一信号样本，若其真实值为： $[y_1,y_2,y_3,y_4]$，模型预测概率值为：$[a_1,a_2,a_3,a_4]$，那么该模型的评价指标 $abs-sum$ 为：

$$abs-sum=\sum _{j=1}^n\sum _{i=1}^4\left|y{}_i-a{}_i\right|$$
例如，某心跳信号类别为 $1$，通过独热编码 (One-Hot Encoding) 转成 $[0,1,0,0]$，预测不同心跳信号概率为 $[0.1,0.7,0.1,0.1]$，那么这个信号预测结果的 $abs-sum$ 为：

$$abs-sum=\left|0.1-0\right|+\left|0.7-1\right|+\left|0.1-0\right|+\left|0.1-0\right|=0.6$$

以上，示范了 4 分类的 $abs-sum$ 评价方式。为更进一步了解常用分类评价指标，以下将依次对混淆矩阵，召回率、精确度、准确率、F1 分数等各项指标进行回顾。

其实，多分类评价指标的计算方式与二分类基本一致，只不过计算的是针对于每一类而言的。

1) 混淆矩阵 (Confuse Matrix)

• 若一个样本是正类 (P)，并且被分类预测为正类 (P)，即为 真正类 TP (True Positive)
• 若一个样本是正类 (P)，但是被分类预测为负类 (N)，即为 假负类 FN (False Negative) (II 类错误)
• 若一个样本是负类 (N)，但是被分类预测为正类 (P)，即为 假正类 FP (False Positive) (I 类错误)
• 若一个样本是负类 (N)，并且被分类预测为负类 (N)，即为 真负类 TN (True Negative)

其中，第一个字母 T/F，表示预测的正确与否；第二个字母 P/N，表示预测为正例或负例。例如，TP 表示把正样本正确地分类为正类 P。换言之，所预测的正样本确为真的正样本。可见，样本总数 = TP + TN + FP + FN。

现在，不妨以医院检测为例进一步说明。设阴性样本 (正常) 为正例 (P)，阳性样本 (有疾) 为负例 (N)。TP 和 TN 表示检测试剂准确，将阴性样本正确检测为阴性 (TP)，将阳性样本正确检测为阴性 (TP)；FP 和 FN 则说明检测试剂有误，把病人检测为正常人 (FP)，把正常人检测成病人 (FN)。显然，在医疗检测的场景当中，假阳 (FN) 尚可以接受，假阴 (FP) 则绝对不允许。因为假阳 (FN) 还可以再检测，以确认是真阳 (TN) 还是假阳 (FN)；但如果是假阴 (FP)，则不但会放过真正的病例 (N)，还可能对他人造成危害。因此，医疗检测试剂会比一般标准更加敏感，以提高召回率，避免出现漏网之鱼。

2) 精确率/查准率 (Precision, P)

精确率 是针对预测结果而言的，表示 分类正确的正样本数 (TP) 占 预测为正样本的总样本数 (TP + FP) 的比例，其定义为：

$$Precision=\frac{TP}{TP+FP}$$

可见， 精确率反映了所有分类器判断为正例的样本 (TP + FP) 中，真的正样本 (TP) 所占的比例。

3) 召回率/查全率 (Recall, R)

召回率 是针对原样本而言的，表示 分类正确的正样本数 (TP) 占 实际的正样本总数 (TP + FN) 的比例，其定义为：

$$Recall=\frac{TP}{TP+FN}$$
可见， 召回率反映了所有实际的正样本 (TP + FN) 中，真的正样本 (TP) 所占的比例。

关于精确率和召回率，以找文章为例。假设，共有 10 篇文章，其中 4 篇是需要找的。通过算法模型，找到了 5 篇，但实际上在这 5 篇中，只有 3 篇是真正需要的。此时，算法的精确率是 3 / 5 = 60%，意即找的这 5 篇，有 3 篇是真正对的；算法的召回率是 3 / 4 =75%，意即需要找的 4 篇文章，找到了其中 3 篇。

理想时，精确率和召回率二者都越高越好。然而，二者实际是一对 矛盾 的度量：精确率高时，召回率低；精确率低时，召回率高。一个原因是 样本存在误差，尤其是临界边缘的数据由于存在误差，导致互相渗透；另一个原因是 模型拟合能力有限，非线性模型以超平面划分样本，若扩大召回，可能导致混入更多错误样本，若提升精度，必然召回会下降。因此，以精确率还是召回率作评价指标，需具体问题具体分析。

4) 准确率 (Accuracy)

准确率 是最常用的评价指标之一，表示 分类正确的总样本数 (TP + TN) 占 总样本数 (TP + TN + FP + FN) 的比例，其定义为：

$$Accuracy=\frac{N_{Correct}}{N_{Total}}=\frac{TP+TN}{TP+TN+FP+FN}$$

然而，准确率不适合样本不均衡的情况，医疗数据大部分都是样本不均衡数据。准确率和精确率看似相近，实则不同：精确率 代表 对正样本结果中的预测正确程度，准确率 则代表 对所有样本的预测正确程度，包括正、负样本。此外，相比于总为 二分类 指标的 精确率，准确率 能从二分类推广和应用到 多分类。

5) 宏精确率/宏查准率 (macro-P)

宏精确率 计算每个样本的精确率然后求平均值

$$macroP=\frac{1}{n}\sum _1^{n}p{}_i$$

6) 宏召回率/宏查全率 (macro-R)

** 宏召回率** 计算每个样本的召回率然后求平均值

$$macroR=\frac{1}{n}\sum _1^{n}R{}_i$$

7) 宏 F1 (macro-F1)

$$macro{F}_1=\frac{2\times macroP\times macroR}{macroP+macroR}$$

与上述的 “宏” 不同，微精确率 (micro-P) 和微召回率 (micro-R) 先将多个混淆矩阵的 TP, FP, TN, FN 对应位置求平均，然后按照 P 和 R 的公式求得 micro-P 和 micro-R，最后根据 micro-P 和 micro-R 求得 micro-F1，如下所示：

8) 微精确率/微查准率 (micro-P)

$$microP=\frac{\overline{TP}}{\overline{TP}\times \overline{FP}}$$

9) 微召回率/微查全率 (micro-R)

$$microR=\frac{\overline{TP}}{\overline{TP}\times \overline{FN}}$$

10) 微 F1 (micro-F1)

$$micro{F}_1=\frac{2\times microP\times microR}{microP+microR}$$

1.2.4 赛题分析

• 本题为传统的数据挖掘问题，通过数据科学及机器学习深度学习进行建模和预测。
• 本题为典型的多分类问题，心跳信号共有 4 种不同的类别。
• 主要应用 LightGBM、XGBoost、CatBoost 及 Pandas、Numpy、Matplotlib、Seabon、Sklearn、TensorFlow / Keras
  等数据挖掘常用库或者框架来进行数据挖掘任务。

1.3 Baseline 学习与解读

1.3.1 导入依赖

import os
import gc
import math
import time

import pandas as pd
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt

import lightgbm as lgb
import xgboost as xgb
from catboost import CatBoostClassifier

from sklearn.metrics import log_loss
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold, KFold

import warnings
warnings.filterwarnings('ignore')

1.3.2 读取数据

train = pd.read_csv('./data/train.csv')  # 训练-验证集
test = pd.read_csv('./data/testA.csv')  # 测试集

train.head()  # 查看前 5 条信息

test.head()  # 查看前 5 条信息

# 查看训练-验证集 shape 
train.values.shape   # (100000, 3) 

# 查看第 0 条训练-验证集样本
train.values[0, :] 

# 查看第 0 条训练-验证集样本 的 特征序列长度
len(train.values[0][1].split(','))  # 205

可见，目前只有 3 列数据，除第 1 列的 id 和第 3 列的 labels，主要的特征数据 hrartbeat_signals 都以 1 维信号振幅 (已被归一化至 0～1 了) 序列 (str-ndarray) 的形式集中到了第 2 列，且信号长度均为 205 (表明有 205 个时间节点)。同时，除波形数据外，没有任何辅助或先验信息 可以利用。接下来，需要将其分离为有意义的 205 条特征。

1.3.3 数据预处理

1) 精度量化压缩

def reduce_mem_usage(df):
	''' 
	数据精度量化压缩函数 
	'''
    # 处理前 数据集总内存计算
    start_mem = df.memory_usage().sum() / 1024**2 
    print('Memory usage of dataframe is {:.2f} MB'.format(start_mem))
    
    # 遍历特征列
    for col in df.columns:
        # 当前特征类型
        col_type = df[col].dtype
        # 处理 numeric 型数据
        if col_type != object:
            c_min = df[col].min()  # 最小值
            c_max = df[col].max()  # 最大值
            # int 型数据 精度转换
            if str(col_type)[:3] == 'int':
                if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
                    df[col] = df[col].astype(np.int8)
                elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
                    df[col] = df[col].astype(np.int16)
                elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
                    df[col] = df[col].astype(np.int32)
                elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
                    df[col] = df[col].astype(np.int64)  
            # float 型数据 精度转换
            else:
                if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
                    df[col] = df[col].astype(np.float16)
                elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
                    df[col] = df[col].astype(np.float32)
                else:
                    df[col] = df[col].astype(np.float64)
        # 处理 object 型数据
        else:
            df[col] = df[col].astype('category')  # object 转 category
    
    # 处理后 数据集总内存计算
    end_mem = df.memory_usage().sum() / 1024**2 
    print('Memory usage after optimization is: {:.2f} MB'.format(end_mem))
    print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem) / start_mem))
    
    return df

# 训练-验证集量化压缩

# 训练-验证集列表
train_list = [] 
# 遍历每一条样本，分离信号数据作为独立特征 (id + 205 beats + label)
for items in train.values:
    train_list.append([items[0]] + [float(i) for i in items[1].split(',')] + [items[2]])
# 数据类型转换 list -> numpy -> DataFrame
train = pd.DataFrame(np.array(train_list))
# 特征名构造 id + s_0 ~ s_205 + label
train.columns = ['id'] + ['s_' + str(i) for i in range(len(train_list[0])-2)] + ['label']
# 内存优化
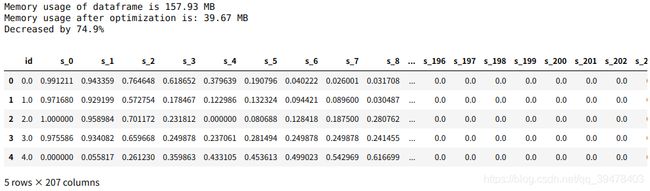
train = reduce_mem_usage(train)
# 查看
train.head()

# 同理，对测试集量化压缩
test_list=[]
for items in test.values:
    test_list.append([items[0]] + [float(i) for i in items[1].split(',')])
test = pd.DataFrame(np.array(test_list))
test.columns = ['id'] + ['s_'+str(i) for i in range(len(test_list[0])-1)]
test = reduce_mem_usage(test)
test.head()  # without labels

可见，压缩率较高，有效地降低了内存占用而不会对训练精度造成过大负面影响。事实上，对于连续型数值特征，有时太高的精度可能也是一种噪声，故 可以在保留重要信息的前提下对其精度截断/量化处理。

2) 简单探查分析

首先，分别查看训练-验证集和测试集的统计信息：

train.describe()

test.describe()

其次，分别查看训练-验证集和测试集的基本信息：

train.info()

test.info()

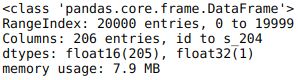
可见，波形数据均已被量化为 float16 类型的数值型特征，且 没有类别型特征需要考虑。

再次，检查是否存在缺失值：

list(train.isna().any())  # 为避免信息太长被省略显示, 可转换为 Python-list 完整查看

检查后，没有缺失值，也就无需填充了，非常理想。事实上，未采集到的信号默认振幅就是 0，故不存在缺失值的问题。更何况，除 ID3 外，大部分的树模型都能够自动处理缺失值，而我们基本都会用到树模型。

接着，不妨通过 KDE 进行训练-验证集与测试集的 分布一致性检查：

# 此处选择采用 核密度估计 (Kernel Density Estimation, KDE) 查看和对比数据分布
dist_cols = 6  # 子图总数：35 行 * 6 列
dist_rows = 35
plt.figure(figsize=(20, 20))  # 每幅子图尺寸： 20 * 20

for i, col in enumerate(test.columns):
    ax = plt.subplot(dist_rows, dist_cols, i+1)
    ax = sns.kdeplot(train[col], color="Red", shade=True)  
    ax = sns.kdeplot(test[col], color="Blue", shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train", "test"])
plt.show()

可见，没有设好距离导致我的图被吃了了一半 训练-验证集和测试集的分布十分接近，基本符合 训练样本和测试样本来自同一分布 的假设，相当理想。这意味着 通过添加噪声进行数据增强的方式很可能并不十分有效。

最后，查看训练-验证集的 类别频数/分布：

plt.hist(train['label'], orientation = 'vertical', histtype = 'bar', color = 'red')
plt.show() 

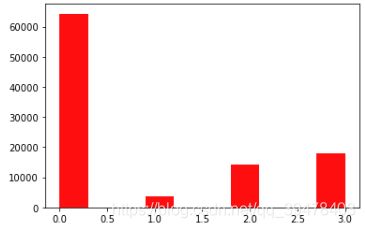
可见，训练-验证集中存在 严重的类别不平衡问题。通常，不平衡问题处理方式包括：

1. 对少样本过采样
2. 对大样本欠采样
3. 合成新的少数类样本
4. 调整类别标签权重

例如，通过 SMOTE 对少数类别样本过采样：

from imblearn.over_sampling import SMOTE   
#from imblearn.under_sampling import RandomUnderSampler 
     
y_train = train['label']
x_train = train.drop(['id','label'], axis=1)

#smote = SMOTE({1.0:30000, 2.0:30000, 3.0:30000}, random_state=2021, n_jobs=-1)  # 指定过采样数量
smote = SMOTE(random_state=2021, n_jobs=-1)
x_smote, y_smote = smote.fit_resample(x_train, y_train)

然后，查看过采样后各类别样本数：

plt.hist(y_smote, orientation = 'vertical', histtype = 'bar', color = 'blue')
plt.show() 

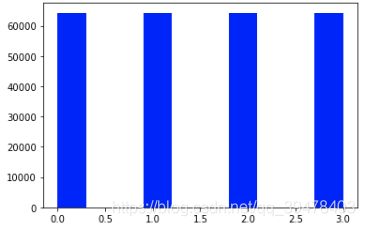
此时，虽然类别不平衡问题暂时是解决了，但这样做的负面影响在于：样本数过多将降低训练速度、基于插值的过采样可能导致过拟合等。

接下来，绘制训练-验证集中各类别样本的一个波形示例简单观察一下：

fig, ax = plt.subplots(nrows=4, ncols=1, figsize=(10, 15))
colors = ['red', 'orange' ,'skyblue', 'lightgreen']
for i in range(4):
    ax[i].plot(range(0, 205), train[train['label']==i].sample(1).iloc[0, 1:206], color=colors[i]) 
    ax[i].set_title(f'Class: {i}')

可见，每种类别或者说各类病症的心跳波形都具有各自的特点，比如起搏频率、位置，振幅高低等，可能局部或全局都有重要的特征可以挖掘。这里的数据似乎是心电图中一个周期的心跳，因为没有看到规律而周期呈现的波形，故对其进行特征工程时 无需考虑其周期性。另一方面，数据中没有显著的噪声、突起和畸变，似乎 无需滤波。此外，还可以多绘制几条同类别样本曲线，以观察各波形的共性和个性，从而更有针对性地进行分析、处理和设计。

1.3.4 准备训练

# data 与 id / label 分离
y_train = train['label']
x_train = train.drop(['id','label'], axis=1)
x_test = test.drop(['id'], axis=1)

# 自定义评分函数
def abs_sum(y_pred, y_true):
    y_pred = np.array(y_pred)
    y_true = np.array(y_true)
    loss = sum(sum(abs(y_pred-y_true)))
    return loss

def cv_model(clf, train_x, train_y, test_x, clf_name):
	''' 
	5-fold 交叉验证 训练模型 函数
	'''
    seed = 2021   # 随机数种子
    test = np.zeros((test_x.shape[0],4))  # 测试集预测结果记录
    cv_scores = []  # 交叉验证得分记录
    onehot_encoder = OneHotEncoder(sparse=False)  # 独热编码 处理 label
    
    kf = KFold(n_splits=5, shuffle=True, random_state=seed)  # 5-fold CV
    for i, (train_index, valid_index) in enumerate(kf.split(train_x, train_y)):
        print(f'************************************ fold - {str(i+1)} ************************************')
        # 当前 fold 的训练-验证集分离
        trn_x, trn_y, val_x, val_y = train_x.iloc[train_index], train_y[train_index], train_x.iloc[valid_index], train_y[valid_index]
        # lightbgm
        if clf_name == "lgb":
        	# 构造数据类型
            train_matrix = clf.Dataset(trn_x, label=trn_y)
            valid_matrix = clf.Dataset(val_x, label=val_y)
			# 设定模型参数
            params = {
                'boosting_type': 'gbdt',    # GBDT 算法
                'objective': 'multiclass',  # 多分类目标函数
                'num_class': 4,  		    # 4 分类
                'num_leaves': 2 ** 5,
                'feature_fraction': 0.8,
                'bagging_fraction': 0.8,
                'bagging_freq': 4,
                'learning_rate': 0.1,       # 学习率 / 步长
                'seed': seed,			    # 随机数种子
                'nthread': 28,              # 运行时线程数 
                'n_jobs':-1,                # 并行运行的多线程数
                'verbose': -1}
		    # 训练/拟合模型
            model = clf.train(
            	params, 
                train_set=train_matrix, 
                valid_sets=valid_matrix, 
                num_boost_round=2000, 
                verbose_eval=100, 
                early_stopping_rounds=200)
            # 预测验证集和测试集
            val_pred = model.predict(val_x, num_iteration=model.best_iteration)
            test_pred = model.predict(test_x, num_iteration=model.best_iteration) 
         
        # 对 label 独热编码以适应自定义评分函数的计算
        val_y = np.array(val_y).reshape(-1, 1)
        val_y = onehot_encoder.fit_transform(val_y)
        print('预测的概率矩阵为：')
        print(test_pred)
        
        # 记录预测结果
        test += test_pred
        score = abs_sum(val_y, val_pred)
        cv_scores.append(score)
        print(cv_scores)
       
    # 最终结果输出
    print("*******************************************************************************************")
    print(f"{clf_name}_cv_score_train_list: {cv_scores}")
    print(f"{clf_name}_cv_score_mean: {np.mean(cv_scores)}")
    print(f"{clf_name}_cv_score_std: {np.std(cv_scores)}")
    
    # 取均值
    test = test / kf.n_splits

    return test

# 构造模型
def lgb_model(x_train, y_train, x_test):
    lgb_test = cv_model(lgb, x_train, y_train, x_test, "lgb")
    return lgb_test

# 训练
lgb_test = lgb_model(x_train, y_train, x_test)

1.3.5 处理提交

注意，正式准备提交前，一定要先检查一下预测结果是否存在问题（如没处理好变量名对应，导致结果值全为 0；多出或少了若干行，导致结果没对齐等）再提交，不要训练提交一把梭，否则可能白白浪费宝贵的提交次数。

# 生成提交文件
temp = pd.DataFrame(lgb_test)
# 检查
temp

# 读取提交模板
result = pd.read_csv('./prediction_result/sample_submit.csv')
# 拷贝测试集预测结果到提交模板中
result['label_0'] = temp[0]
result['label_1'] = temp[1]
result['label_2'] = temp[2]
result['label_3'] = temp[3]
# 生成提交文件
result.to_csv('./prediction_result/submit.csv', index=False)

1.4 后话

一方面，此处仅仅对 Baseline 进行了简单解读，旨在理解并跑通大致的流程。至于 Baseline 的效果一般，则是因为还没有进行后续充分而有效的 EDA、特征工程、集成学习 等重要步骤。其中，特征工程最体现技术且最具挑战性。

另一方面，很感谢组队学习三月营的大佬们提供的 Baseline 以及耐心的答疑解惑，因为逻辑清晰的 Baseline 以及颇具建设性的指导意见能够节约不少时间精力，对我们萌新有很大帮助 ^ O ^

夜深了，不要熬夜，明天起来再学习吧～