sklearn.metrics模块重要API总结（持续更新）

前言

平时训练模型，会写一些评估函数，简单的评估函数如准确率等很容易实现，当使用AUC、NDCG等指标时，调用sklearn.metrics不仅准确可靠，而且速度飞快。

sklearn有三种不同的度量：

• Estimator score method：估计器有一个评分方法，为他们要解决的问题提供默认的评估标准。
• Scoring parameter：模型评估工具使用交叉验证（如model_selection.cross_val_score和model_selection.GridSearchCV）依赖于内部评分策略。
• Metric functions：sklearn.metrics 模块实现了为特定目的评估预测误差的功能。这些指标在分类指标(Classification metrics)、多标签排名指标(Multilabel ranking metrics)、回归指标(Regression metrics)和聚类指标(Clustering metrics)部分中有详细说明。

本节主要就是介绍Metric functions。

参考资料：
sklearn.metrics官方文档

各类指标

sklearn.metrics一个package，包含评分函数(score functions)、性能指标(性能指标)、pairwise metrics和距离计算(distance computations)。

分类指标（Classification metrics）

Precision-Recall系列

• sklearn.metrics.precision_score
• sklearn.metrics.recall_score

precision简称为$\text{P}$，分为 $\text{macro-P}$、$\text{micro-P}$、$\text{weighted-P}$

二分类

西瓜书上说的就是二分类，其：

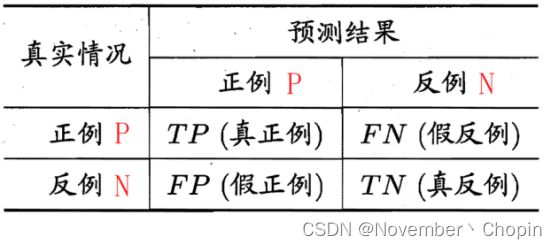
查准率（Precision）：$P=\frac{TP}{TP+FP}$，挑出的西瓜中，有多少比例是好瓜。

查全率（Recall）：$R=\frac{TP}{TP+FN}$，所有好瓜中，有多少比例被挑出来。

F1：$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样本总数+TP-TN}$，P和R的调和平均数。

from sklearn.metrics import precision_score, recall_score,f1_score
y_true = [0, 0, 1, 1, 1, 1]
y_pred = [0, 1, 0, 1, 0, 1]

precision_score(y_true, y_pred)
"""
输出：0.6666666666666666
TP=2, FP=1
根据公式可得P=2/(2+1)=2/3
"""
recall_score(y_true, y_pred) # 同理
f1_score(y_true, y_pred) # 同理

多分类

多标签分类

sklearn.metrics.accuracy_score

准确度分类得分。为样本预测的标签集必须与y_true中的相应标签集完全匹配。也可以给样本加权，详见sklearn.metrics.accuracy_score文档

accuracy_score(y_true, y_pred)

y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
accuracy_score(y_true, y_pred)
"""
输出:
0.5
"""

sklearn.metrics.auc

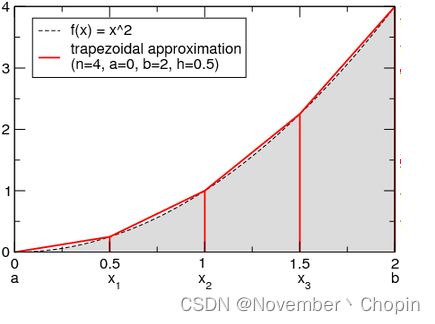
使用梯形法则(trapezoidal rule)求曲线下的面积“Area Under the Curve (AUC) ”。这是一个通用的求曲线下面积的函数，只需要给定曲线上的点。要计算ROC曲线下的面积，使用roc_auc_score。

简单来说，这就是一个根据梯形法则逼近曲线在区间内的积分，比如我们计算 $y=x^2$ 在区间 $[0,2]$ 内的面积，通过牛顿-莱布尼茨公式可以计算出其面积为 $\frac{8}{3}$，我们只需要给定 $y=x^2$ 曲线在 $[0,1]$ 上的点，就可以用梯形法则逼近其区间内的面积，见如下图片及代码部分（图片来源于南安普顿大学）。

sklearn.metrics.auc(x, y)
x：x坐标，要么是单调递增，要么是单调递减。
y：y坐标。

import numpy as np
from sklearn import metrics
# n越大，结果越精确
n = 10000000
x = np.linspace(0,2,n)
y = x**2
metrics.auc(x, y)
"""
输出:
2.6666666666666803
"""

average_precision_score (AP)

计算平均查准率(average precision, AP)。

说到AP，就不得

$$\text{AP}=\sum _n(R_n-R_{n-1})P_n$$

回归指标（Regression metrics）

多标签排序指标（Multilabel ranking metrics）

聚类指标（Clustering metrics）

双聚类指标（Biclustering metrics）

距离指标（Distance metrics）

Pairwise metrics

绘图