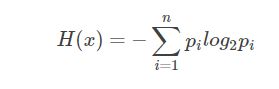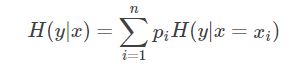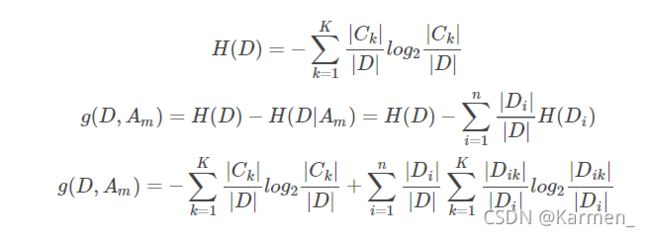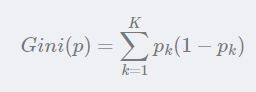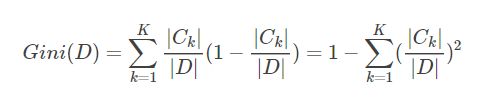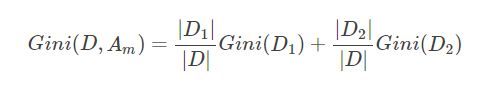机器学习（三）西瓜决策树

〇. ID3决策树算法原理

1. 纯度 purity

对于一个分支结点，如果该结点所包含的样本都属于同一类，那么它的纯度为1，而我们总是希望纯度越高越好，也就是尽可能多的样本属于同一类别。那么如何衡量“纯度”呢？由此引入“信息熵”的概念。

2. 信息熵 information ertropy

假定当前样本集合D中第k类样本所占的比例为pk（k=1,2,…,|y|），则D的信息熵定义为：

Ent(D) = -∑k=1 pk·log2 pk (约定若p=0，则log2 p=0)

显然，Ent(D)值越小，D的纯度越高。因为0<=pk<= 1,故log2 pk<=0，Ent(D)>=0. 极限情况下，考虑D中样本同属于同一类，则此时的Ent(D)值为0（取到最小值）。当D中样本都分别属于不同类别时，Ent(D)取到最大值log2 |y|.

3. 信息增益 information gain

假定离散属性a有V个可能的取值{a1,a2,…,aV}. 若使用a对样本集D进行分类，则会产生V个分支结点，记Dv为第v个分支结点包含的D中所有在属性a上取值为av的样本。不同分支结点样本数不同，我们给予分支结点不同的权重：|Dv|/|D|, 该权重赋予样本数较多的分支结点更大的影响、由此，用属性a对样本集D进行划分所获得的信息增益定义为：

Gain(D,a) = Ent(D)-∑v=1 |Dv|/|D|·Ent(Dv)

其中，Ent(D)是数据集D划分前的信息熵，∑v=1 |Dv|/|D|·Ent(Dv)可以表示为划分后的信息熵。“前-后”的结果表明了本次划分所获得的信息熵减少量，也就是纯度的提升度。显然，Gain(D,a) 越大，获得的纯度提升越大，此次划分的效果越好。

4. 增益率 gain ratio

基于信息增益的最优属性划分原则——信息增益准则，对可取值数据较多的属性有所偏好。C4.5算法使用增益率替代信息增益来选择最优划分属性，增益率定义为：

Gain_ratio(D,a) = Gain(D,a)/IV(a)

其中IV(a) = -∑v=1 |Dv|/|D|·log2 |Dv|/|D|

称为属性a的固有值。属性a的可能取值数目越多（即V越大），则IV(a)的值通常会越大。这在一定程度上消除了对可取值数据较多的属性的偏好。

事实上，增益率准则对可取值数目较少的属性有所偏好，C4.5算法并不是直接使用增益率准则，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

5. 基尼指数 Gini index

CART决策树算法使用基尼指数来选择划分属性，基尼指数定义为：

Gini(D) = ∑k=1; ∑k’≠1; pk·pk’ = 1- ∑k=1 pk·pk

Gini index从数据集D中随机抽取两个样本，类别标记不一致概率。Gini越小，纯度越高。

即使用基尼指数选择最优划分属性，即选择使得划分后基尼指数最小的属性做为最优划分属性。

属性a的基尼指数：Gain_index(D,a) = ∑v=1 |Dv|/|D|·Gini(Dv)

一、ID3算法代码

1. 引入数据和需要用到的包：

import numpy as np
import pandas as pd
import sklearn.tree as st
import math
import matplotlib					#引入绘图包
import matplotlib.pyplot as plt		#

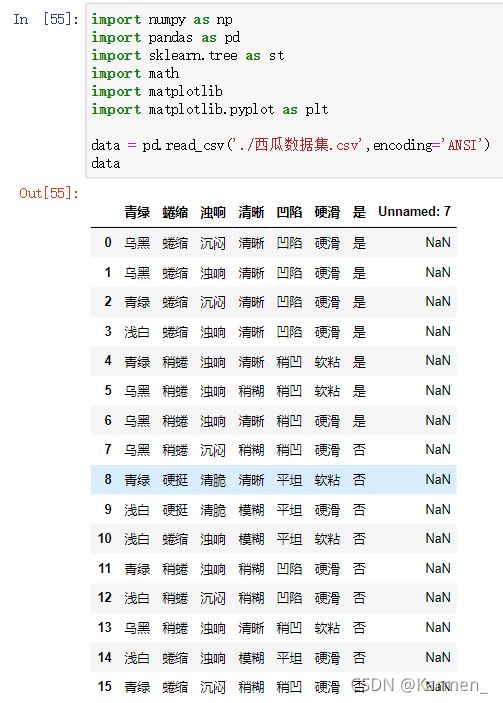
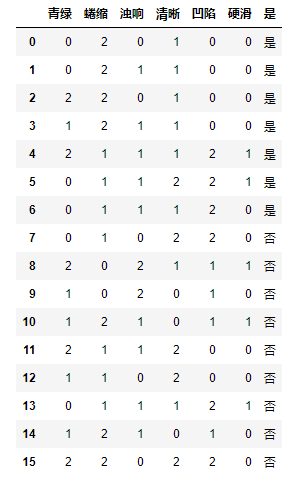
data = pd.read_csv('./西瓜数据集.csv',encoding='ANSI')		#读取数据集 采用ANSI编码
data = data.loc[:, ~data.columns.str.contains('Unnamed')]	#删除多出来的uname一行
data

读取数据的代码虽然少，但同时也是很重要的一步，如果数据读错了，那后面的结果也都是错的。

所以这里我会记录几个比较常见的问题：

• 数据集是txt格式的文件，如何将其转换成csv

txt的数据文件中，各个数据会由逗号或者空格来分开，而csv就是由逗号分隔数据的表格形的txt文件，所以得先将txt文本中的分隔符全部用半角的逗号替换掉，然后再另存为，选择ANSI编码格式生成新的txt文件，最后直接改后缀名为csv，如果编码格式选错了会导致乱码！（不要问为什么，它就是这么规定的）

错误①：不换分隔符直接暴力改后缀的结果：

错误②：换了分隔符但没有更换编码格式导致的结果：

• read_csv时没有备注encoding

读取文件时默认编码格式并不是ANSI，这样就会导致读到Python程序里时又成了乱码，所以这里切记要加上encoding='ANSI'

• 莫名其妙多出一列Unnamed：x

多出一行后导致的最终结果完全错误：

为什么会出现Unnamed列原因我也不知道，但我知道如何解决这个问题

data = data.loc[:, ~data.columns.str.contains('Unnamed')]

加上这个万能代码删除带有Unnamed字符串的列，这个方法还能用来应对垃圾数列。

2. 算法函数

计算熵

def calcEntropy(dataSet):
    mD = len(dataSet)
    dataLabelList = [x[-1] for x in dataSet]
    dataLabelSet = set(dataLabelList)
    ent = 0
    for label in dataLabelSet:
        mDv = dataLabelList.count(label)
        prop = float(mDv) / mD
        ent = ent - prop * np.math.log(prop, 2)

    return ent

拆分数据集

# index - 要拆分的特征的下标
# feature - 要拆分的特征
# 返回值 - dataSet中index所在特征为feature，且去掉index一列的集合
def splitDataSet(dataSet, index, feature):
    splitedDataSet = []
    mD = len(dataSet)
    for data in dataSet:
        if(data[index] == feature):
            sliceTmp = data[:index]
            sliceTmp.extend(data[index + 1:])
            splitedDataSet.append(sliceTmp)
    return splitedDataSet

选择最好的特征

# 返回值 - 最好的特征的下标
def chooseBestFeature(dataSet):
    entD = calcEntropy(dataSet)
    mD = len(dataSet)
    featureNumber = len(dataSet[0]) - 1
    maxGain = -100
    maxIndex = -1
    for i in range(featureNumber):
        entDCopy = entD
        featureI = [x[i] for x in dataSet]
        featureSet = set(featureI)
        for feature in featureSet:
            splitedDataSet = splitDataSet(dataSet, i, feature)  # 拆分数据集
            mDv = len(splitedDataSet)
            entDCopy = entDCopy - float(mDv) / mD * calcEntropy(splitedDataSet)
        if(maxIndex == -1):
            maxGain = entDCopy
            maxIndex = i
        elif(maxGain < entDCopy):
            maxGain = entDCopy
            maxIndex = i

    return maxIndex

寻找最多的，作为标签

# 返回值 - 标签
def mainLabel(labelList):
    labelRec = labelList[0]
    maxLabelCount = -1
    labelSet = set(labelList)
    for label in labelSet:
        if(labelList.count(label) > maxLabelCount):
            maxLabelCount = labelList.count(label)
            labelRec = label
    return labelRec

生成树

def createFullDecisionTree(dataSet, featureNames, featureNamesSet, labelListParent):
    labelList = [x[-1] for x in dataSet]
    if(len(dataSet) == 0):
        return mainLabel(labelListParent)
    elif(len(dataSet[0]) == 1): #没有可划分的属性了
        return mainLabel(labelList)  #选出最多的label作为该数据集的标签
    elif(labelList.count(labelList[0]) == len(labelList)): # 全部都属于同一个Label
        return labelList[0]

    bestFeatureIndex = chooseBestFeature(dataSet)
    bestFeatureName = featureNames.pop(bestFeatureIndex)
    myTree = {bestFeatureName: {}}
    featureList = featureNamesSet.pop(bestFeatureIndex)
    featureSet = set(featureList)
    for feature in featureSet:
        featureNamesNext = featureNames[:]
        featureNamesSetNext = featureNamesSet[:][:]
        splitedDataSet = splitDataSet(dataSet, bestFeatureIndex, feature)
        myTree[bestFeatureName][feature] = createFullDecisionTree(splitedDataSet, featureNamesNext, featureNamesSetNext, labelList)
    return myTree

初始化

# 返回值
# dataSet 数据集
# featureNames 标签
# featureNamesSet 列标签
def readWatermelonDataSet():
    dataSet = data.values.tolist()
    featureNames =['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']
    #获取featureNamesSet
    featureNamesSet = []
    for i in range(len(dataSet[0]) - 1):
        col = [x[i] for x in dataSet]
        colSet = set(col)
        featureNamesSet.append(list(colSet))
    
    return dataSet, featureNames, featureNamesSet

画图

# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']

# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")

# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")

# 箭头样式
arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    绘制一个节点
    :param nodeTxt: 描述该节点的文本信息
    :param centerPt: 文本的坐标
    :param parentPt: 点的坐标，这里也是指父节点的坐标
    :param nodeType: 节点类型,分为叶子节点和决策节点
    :return:
    """
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    """
    获取叶节点的数目
    :param myTree:
    :return:
    """
    # 统计叶子节点的总数
    numLeafs = 0

    # 得到当前第一个key，也就是根节点
    firstStr = list(myTree.keys())[0]

    # 得到第一个key对应的内容
    secondDict = myTree[firstStr]

    # 递归遍历叶子节点
    for key in secondDict.keys():
        # 如果key对应的是一个字典，就递归调用
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        # 不是的话，说明此时是一个叶子节点
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    """
    得到数的深度层数
    :param myTree:
    :return:
    """
    # 用来保存最大层数
    maxDepth = 0

    # 得到根节点
    firstStr = list(myTree.keys())[0]

    # 得到key对应的内容
    secondDic = myTree[firstStr]

    # 遍历所有子节点
    for key in secondDic.keys():
        # 如果该节点是字典，就递归调用
        if type(secondDic[key]).__name__ == 'dict':
            # 子节点的深度加1
            thisDepth = 1 + getTreeDepth(secondDic[key])

        # 说明此时是叶子节点
        else:
            thisDepth = 1

        # 替换最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth

    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):
    """
    计算出父节点和子节点的中间位置，填充信息
    :param cntrPt: 子节点坐标
    :param parentPt: 父节点坐标
    :param txtString: 填充的文本信息
    :return:
    """
    # 计算x轴的中间位置
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    # 计算y轴的中间位置
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    # 进行绘制
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    """
    绘制出树的所有节点，递归绘制
    :param myTree: 树
    :param parentPt: 父节点的坐标
    :param nodeTxt: 节点的文本信息
    :return:
    """
    # 计算叶子节点数
    numLeafs = getNumLeafs(myTree=myTree)

    # 计算树的深度
    depth = getTreeDepth(myTree=myTree)

    # 得到根节点的信息内容
    firstStr = list(myTree.keys())[0]

    # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)

    # 绘制该节点与父节点的联系
    plotMidText(cntrPt, parentPt, nodeTxt)

    # 绘制该节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)

    # 得到当前根节点对应的子树
    secondDict = myTree[firstStr]

    # 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴
    plotTree.yOff = plotTree.yOff - 2/plotTree.totalD

    # 循环遍历所有的key
    for key in secondDict.keys():
        # 如果当前的key是字典的话，代表还有子树，则递归遍历
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/W
            plotTree.xOff = plotTree.xOff + 2.0/plotTree.totalW
            # 打开注释可以观察叶子节点的坐标变化
            # print((plotTree.xOff, plotTree.yOff), secondDict[key])
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制叶子节点和父节点的中间连线内容
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))

    # 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴
    plotTree.yOff = plotTree.yOff + 2.0/plotTree.totalD


def createPlot(inTree):
    """
    需要绘制的决策树
    :param inTree: 决策树字典
    :return:
    """
    # 创建一个图像
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 计算出决策树的总宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    # 计算出决策树的总深度
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2W
    plotTree.xOff = -1/plotTree.totalW
    # 初始的y轴偏移量，每次向下或者向上移动1/D
    plotTree.yOff = 1.0
    # 调用函数进行绘制节点图像
    plotTree(inTree, (0.5, 1.0), '')
    # 绘制
    plt.show()

输出图像

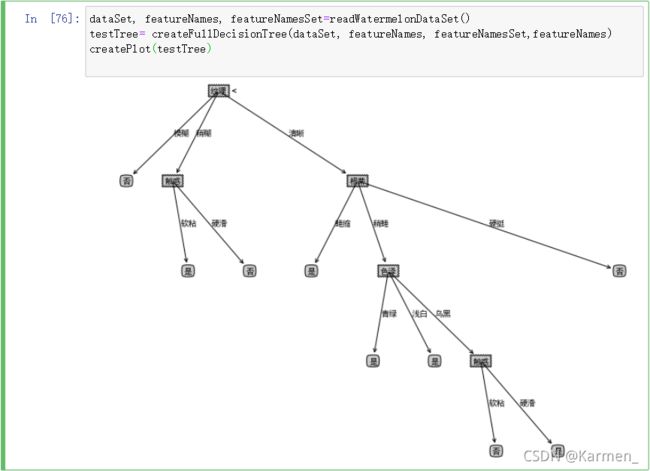
dataSet, featureNames, featureNamesSet=readWatermelonDataSet()
testTree= createFullDecisionTree(dataSet, featureNames, featureNamesSet,featureNames)
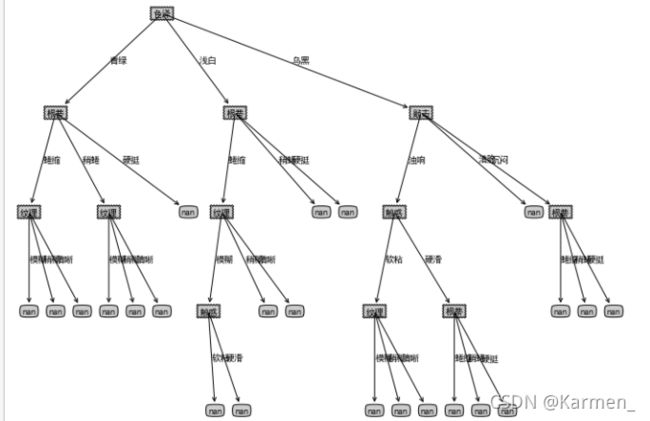
createPlot(testTree)

3. 结果

二、基于sklearn库的实现ID3、CART算法

1. 导入包并读取数据

import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier
data = pd.read_csv('./西瓜数据集.csv',encoding='ANSI')
data = data.loc[:, ~data.columns.str.contains('Unnamed')]
data

2. 数据编码

#创建LabelEncoder()对象，用于序列化
label = LabelEncoder()    

#为每一列序列化
for col in data[data.columns[:-1]]:
    data[col] = label.fit_transform(data[col])
data

---

3. ID3

ID3算法的基本流程为：如果某一个特征能比其他特征更好的将训练数据集进行区分，那么将这个特征放在初始结点，依此类推，初始特征确定之后，对于初始特征每个可能的取值建立一个子结点，选择每个子结点所对应的特征，若某个子结点包含的所有样本属于同一类或所有特征对其包含的训练数据的区分能力均小于给定阈值，则该子结点为一个叶结点，其类别与该叶结点的训练数据类别最多的一致。重复上述过程直到特征用完或者所有特征的区分能力均小于给定阈值。
如何衡量某个特征对训练数据集的区分能力呢，ID3算法通过信息增益来解决这个问题。

信息增益：

一个离散型随机变量xx的概率分布为：P(x=xi)=pi,(i=1,⋯,n)P(x=xi)=pi,(i=1,⋯,n)，那么xx的熵定义如下：

熵的单位为比特(bit)，定义0log0=00log0=0。对于两个随机变量x,yx,y，他们有如下形式的联合概率分布：

那么在 xx确定的条件下yy的条件熵定义如下：

数据集D的熵为H(D)，其关于其某个特征Am的条件熵为H(D|Am)，则信息增益为g(D,Am)=H(D)−H(D|Am)g(D,Am)=H(D)−H(D|Am)。

对于训练样本集来说，其概率是由数据估计得到的，因此其熵与条件熵分别称为经验熵和经验条件熵。经验熵和经验条件熵的计算方式如下：

决策树构建
ID3算法构建决策树的过程简单概括起来就是，自根结点开始，选择信息增益最大的特征作为根结点对应的特征，并依据该特征的可能取值将训练数据分配到不同的子结点，对子结点进行同样的操作，若子结点的所有样本属于同一类别或该子结点处所有特征的信息增益均小于给定阈值或无可供选择的特征，那么这个子结点是一个叶结点，将叶结点的样本数量最多的类别作为叶结点的类别。

• 输入：训练数据D={(x1,y1),⋯,(xN,yN)}D={(x1,y1),⋯,(xN,yN)}，特征集AA，信息增益阈值ϵϵ

• 输出：决策树TT

step1 若DD中样本特征为空，那么树TT为一棵单结点树，将样本数最大的类别作为树的类别，返回TT；否则，转到step2。
step2 计算训练集DD关于所有特征的信息增益，若信息增益均小于阈值ϵϵ，则TT是一棵单结点树，将样本数最大的类别作为树的类别，返回TT；否则，转到step3。
step3 选择信息增益最大的特征AmaxAmax作为根结点特征，依据AmaxAmax的所有可能值建立相应子结点，若子结点的样本全部属于同一类别，则子结点为叶结点，将叶结点类别标记为该结点所有样本所属的类别，若所有子结点均为叶结点，返回TT；否则，返回TT并转到step4。
step4 对非叶子结点ii，以DiDi为训练数据集，A=A−{Amax}A=A−{Amax}为特征集，递归地调用step1-step3，返回子树TiTi。

# 采用ID3拟合
dtc = DecisionTreeClassifier(criterion='entropy')
# 进行拟合
dtc.fit(data.iloc[:,:-1].values.tolist(),data.iloc[:,-1].values) 
# 标签对应编码
result = dtc.predict([[0,0,0,0,0,0]])
#拟合结果
result

得到结果：array([‘否’], dtype=object)

---

4. CART

CART算法构造的是二叉决策树，决策树构造出来后同样需要剪枝，才能更好的应用于未知数据的分类。CART算法在构造决策树时通过基尼系数来进行特征选择。

**基尼指数：**若某样本数据分为KK类，数据属于第k类的概率为pkpk，则样本数据的基尼指数定义为：

对于训练样本集DD，其基尼指数如下：

如果样本集合D根据特征Am的取值可以分为两部分D1和D2，那么在特征Am的条件下，D的基尼指数如下：

基尼指数Gini(D)表征着数据集DD的不确定性，而在特征Am的条件下，D的基尼指数则表征着在特征Am确定的条件下D的不确定性，因此基尼指数之差和信息增益及信息增益比一样，可以表征特征Am对数据集D的分类的能力。

决策树构建：

• 输入： 训练数据集DD，特征集AA，结点样本数阈值δδ，基尼指数阈值ϵϵ

• 输出： CART二叉决策树TT

step1 若样本特征集为空，则TT是一棵单节点数，其类别为DD中样本数最多的类，返回TT；否则，转到step2。
step2 对数据集DD，计算特征集AA中所有特征所有可能切分点的基尼指数，若基尼指数的值均小于给定阈值ϵϵ，则TT是一棵单节点数，其类别为DD中样本数最多的类，返回TT；否则，转到step3。
step3 选择基尼指数最小的特征AminAmin和相应切分点αα作为根节点的特征值和切分标准，根据DD中样本是否等于αα（或≤α≤α，或≥α≥α）将DD分为两个子集D1D1和D2D2，将D1D1和D2D2分别分配到两个子结点中，若子结点样本数均小于给定阈值δδ，则该子结点是一个叶结点，若两个子结点均为叶结点，返回T；否则，返回T并转到step4。
step4 对于非叶子结点，令DD等于该子结点所对应的数据集，特征集A=A−{Amin}A=A−{Amin}，递归的调用step1-step3，返回子树TT。

# 采用CART拟合
dtc = DecisionTreeClassifier()
# 进行拟合
dtc.fit(data.iloc[:,:-1].values.tolist(),data.iloc[:,-1].values) 
# 标签对应编码
result = dtc.predict([[0,0,0,1,0,0]])
#拟合结果
result

得到结果：array([‘是’], dtype=object)

---

5. C4.5

C4.5算法的基本流程与ID3类似，但C4.5算法进行特征选择时不是通过计算信息增益完成的，而是通过信息增益比来进行特征选择。

三、参考文章

**醉意丶千层梦：**西瓜决策树-纯算法

茫茫人海一粒沙：[机器学习-Sklearn]决策树学习与总结 （ID3, C4.5, C5.0, CART）

[**jingjishisi：**ID3 C4.5 CART决策树原理及sklearn实现](