ML学习笔记——决策树
决策树
- 引例
- 算法简图
-
- 一些容易纠结的点
- 算法解析
- 算法的基本流程
- 选择最优划分属性
-
- 信息增益
-
- 信息熵(information entropy)
- 信息增益(information gain)
- 增益率(gain ratio)
- 基尼指数
-
- 基尼值(Gini)
- 基尼指数(Gini index)
- 总结三种算法的原理
- 剪枝处理
-
- 预剪枝(prepruning)
-
- 定义
- 优点
- 缺点
- 后剪枝(postpruning)
-
- 定义
- 优点
- 缺点
- 参考书目
引例
本文以一个经典的二分类西瓜问题为例
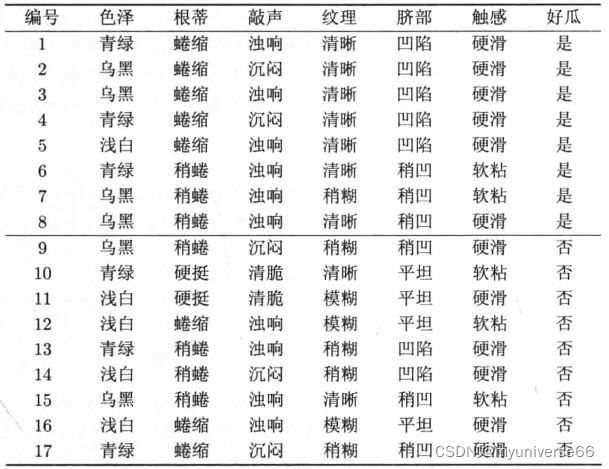
这是一个西瓜训练集D,可以看出,该数据集中共有17组数据,每组数据都有色泽、根蒂、敲声、纹理、脐部、触感6个属性,这6个属性加上其各自的分支(a1色泽:青绿、乌黑、浅白,a2根蒂:蜷缩、稍蜷、硬挺,a3…)组成了该西瓜问题的属性集A。最后,每组数据都会确定其是好瓜还是坏瓜,这就是最终的分类结果。
我们的决策树算法便是在这样一个已有的训练集上构建一个树结构,使得其能够在输入一个新的数据(包含属性集A中的6个属性值)时,能够输出一个最为准确的判断(好瓜还是坏瓜)。
算法简图
一些容易纠结的点
类/类别:就是最终的决策结果(好瓜/坏瓜)
标记为叶结点:即该结点就是最终的决策结点(判定是好瓜还是坏瓜),无法再递归了
算法解析
本质上是一个构建树结构的函数,参数为训练集D和属性集A。可以看出这是一个递归的算法(递归意味着可能有剪枝的方法,后面会讲到)。
递归出口有三个:
(1)当前结点包含的样本全属于同一类别(全是好瓜/全是坏瓜),无需划分,直接做决策;
(2)当前属性集为空(属性集已经用完了),或是所有样本在所有属性上取值相同(在剩下的属性集中,每一个属性的属性值都一样,例:假设对于某次递归的训练子集D,属性集A中只剩下了脐部和触感两个属性,但是D中的西瓜在这两个属性上取值完全一致),无法划分,这时我们以当前结点的训练子集D中最多的分类(好瓜/坏瓜)作为最后的决策结果;
(3)当前结点包含的样本集合为空(在当前递归的训练集D中,该最优划分属性a*的某一分支下无样本),不能划分,此时我们以该叶子结点的父结点的训练集D中最多的分类(好瓜/坏瓜)作为最后的决策结果。
算法的基本流程
决策树算法的核心在于“选择最优划分属性”,根据选择最优划分属性方法的不同主要分为三种算法:
①ID3:以信息增益为准则来选择划分属性
②C4.5:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的
③CART:使用基尼指数来选择划分属性
选择最优划分属性
信息增益
信息熵(information entropy)
熵代表着数据的不确定度,熵越大,不确定度就越大,当数据集的每类数据占比相同时,不确定度最大(例:当训练集D中好瓜和坏瓜的数目相等时,熵最大,为1);当数据集中只有一类数据时,不确定度最小,熵为0。

对本文的西瓜训练集来说,一共有两种分类(好瓜和坏瓜),好瓜有8个,坏瓜有9个,所以p1 = 8/17,p2 = 9/17,运算过程如下:
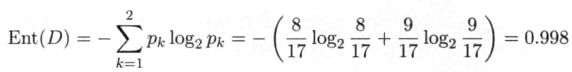
信息增益(information gain)
决策树在构建时其实就是在不断地对数据进行分类,分类之后,信息熵要减小,这个减小的值就叫信息增益。
 |D| 表示训练集D的样本个数
|D| 表示训练集D的样本个数
在本文的西瓜问题中
类似的,我们可计算出其他属性的信息增益∶
Gain(D,根蒂)=0.143; Gain(D,敲声)=0.141;
Gain(D,纹理)=0.381; Gain(D,脐部)=0.289;
Gain(D,触感)=0.006.
显然,属性"纹理"的信息增益最大,于是它被选为划分属性
存在的问题:信息增益对可取值数目较多的属性有所偏好
解释:如果把“编号”作为一个候选划分属性a, 则Ent(Di)=0, 最终Gain(D,a) = Ent(D), 相当于没减。
增益率(gain ratio)
解释:假设某个属性a只有一个D子集(v=1),即对于属性a所有的样本都只有一个类型,则在计算IV(a)时 |Dv| / |D| = 1, 则IV(a) = 0,Gain_ratio(D, a) = +∞。
基尼指数
基尼值(Gini)

直观来说,Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此,Gini(D)越小,则数据集D的纯度越高。
基尼指数(Gini index)
类似于增益率的定义,我们在基尼值的基础上定义基尼指数如下。
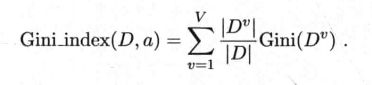
于是,我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性,即CART算法。
总结三种算法的原理
剪枝处理
预剪枝(prepruning)
定义
西瓜书的原文描述:预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
我的理解:在划分每一个结点之前进行一个比较,比较的内容是:对于我们取定的验证集,如果不划分该结点,计算出其验证精度(划分的准确率)x1;如果划分,则计算出划分后的验证精度x2。二者相比:if x1 >= x2 :不划分,else:划分。
优点
①降低了过拟合的风险
②显著减少了决策树的训练时间开销和测试时间开销
缺点
①有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显著提高
②预剪枝基于"贪心"本质禁止这些分支展开,给预剪枝决策树带来了欠拟合的风险
后剪枝(postpruning)
定义
西瓜书的原文描述:后剪枝是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
我的理解:先生成一棵完整的决策树,在这棵树上自底向上进行剪枝操作。对每一个结点的剪枝操作为:与预剪枝类似,如果不剪去该结点,计算出其验证精度x1;如果剪枝,则计算出剪枝后的验证精度x2。二者相比:if x1 >= x2 :不剪枝,else:剪枝。

优点
后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情形下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。
缺点
后剪枝过程是在生成完全决策树之后进行的,并且要自底向上地对树中的所有非叶结点进行逐一考察,因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。
参考书目
《机器学习》周志华著

