第四章 Python数据预处理之划分训练集与测试集

目录

4.1Python代码实现划分训练集和测试集

4.2 交叉验证

4.2.1 交叉验证提出的目的       

4.2.2 留一交叉验证 

 4.2.3 K-折交叉验证

 4.2.3.1 重复随机子抽样验证

4.2.4 嵌套交叉验证

4.2.4.1 k*l 折交叉验证

4.2.4.2 带有验证和测试集的 k 折交叉验证

4.2.4.3 拟合度量

4.2.4.4 时间序列模型的交叉验证    

4.2.5 应用

4.2.6 Python代码实现K-折交叉验证数据集划

---

 4.1Python代码实现划分训练集和测试集

          伪随机函数介绍网站：https://docs.python.org/3/library/random.html。 

# 导入库
from random import seed # 用于固定每次生成的随机数都是确定的（伪随机数）
from random import randrange # 用于生成随机数

def train_test_split(dataset,train=0.6):
    """
    该函数用于划分训练集和测试集
    Parameters
    ----------
    dataset : 二维列表
        传入需要划分成训练集和测试集的数据集.
    train : 浮点数
        传入训练集占整个数据集的比例.默认是0.6.

    Returns
    -------
    train_basket : 二维列表
        划分好的训练集.
    dataset_copy : 二维列表
        划分好的测试集.
    """
    # 创建一个空列表用于存放后面划分好的训练集
    train_basket = list()
    # 根据输入的训练集的比例计算出训练集的大小（样本数量）
    train_size = train*len(dataset)
    # 复制出一个新的数据集来做切分，从而不改变原始的数据集
    dataset_copy = list(dataset)
    # 执行循环判断，如果训练集的大小小于所占的比例，就一直往训练集里添加数据
    while len(train_basket) < train_size:
        # 通过randrange()函数随机产生训练集的索引
        random_choose = randrange(len(dataset_copy))
        # 根据上面生成的训练集的索引将数据集中的样本加到train_basket中
        # 注意pop函数会根据索引将数据集中的样本给移除，所以循环结束之后剩下的样本就是测试集
        train_basket.append(dataset_copy.pop(random_choose))
    return train_basket,dataset_copy


# 主函数
if '__main__' == __name__:
    # 定义一个随机种子，使得每次生成的随机数都是确定的（伪随机数）
    seed(666)
    dataset = [[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]]
    # 调用手动编写的train_test_split函数划分训练集和测试集
    train,test = train_test_split(dataset)

4.2 交叉验证

        有关交叉验证的网站介绍：https://en.wikipedia.org/wiki/Cross-validation_(statistics)#k-fold_cross-validation（注：下面的一些图片转载自该网站，并非原创）。

        交叉验证，[2] [3] [4]有时称为旋转估计[5] [6] [7]或样本外测试，其是一种重采样方法，它使用数据的不同部分在不同的迭代中测试和训练模型。在预测问题中，通常给模型一个已知数据集（训练数据集）和一个用于测试模型的未知数据集（或首次看到的数据）（称为验证数据集或测试）。[8] [9]交叉验证的目标是测试模型预测新数据的能力，以标记过度拟合或选择偏差等问题[10]并深入了解模型将如何推广到独立数据集（即未知数据集，例如来自实际问题）。一轮交叉验证涉及将数据样本划分为互补子集，对一个子集（称为训练集）执行分析，并在另一个子集（称为验证集或测试集）上验证分析。为了减少可变性，在大多数方法中，使用不同的分区执行多轮交叉验证，并将验证结果在各轮中组合（例如求平均准确率）以估计模型的预测性能。总之，交叉验证在预测中结合平均准确率，以得出更准确的模型预测性能。[11]

图1 比较五种分类模型的交叉验证准确率和假阴性（高估）百分比。气泡大小代表交叉验证准确度的标准偏差（十倍）  

4.2.1 交叉验证提出的目的       

        假设一个模型具有一个或多个未知参数，以及一个模型可以拟合的数据集（训练数据集）。拟合过程优化模型参数，使模型尽可能地拟合训练数据。如果从与训练数据相同的群体中获取独立的验证数据样本，通常会证明该模型不适合验证数据而适合训练数据。这种差异的大小可能很大，尤其是当训练数据集的大小很小，或者模型中的参数数量很大时。交叉验证是一种估计这种影响大小的方法。在线性回归中，存在实际目标值 y 1, ..., y n，和n 维向量  x 1 , ..., x n。向量x i的分量表示为x i 1 , ..., x ip。如果使用最小二乘法以超平面 ŷ = a + β T x的形式将函数拟合到数据 ( x i , yi )  1 ≤  i  ≤  n，则可以使用均方误差(MSE) 评估拟合。训练集 ( x i , y i )  1 ≤  i  ≤  n上给定估计参数值a和β的 MSE定义为：

 图2 均方误差公式

        交叉验证可以用于检查模型是否已经过拟合，在这种情况下，验证集中的 MSE 将大大超过其预期值。（线性回归中的交叉验证也很有用，因为它可以用来选择最优的正则化 成本函数）在大多数其他回归过程中（例如逻辑回归)，没有简单的公式来计算预期的样本外拟合。因此，交叉验证是一种普遍适用的方法，可以使用数值计算代替理论分析来预测模型在不可用数据上的性能。

4.2.2 留一交叉验证 

图3 当 n = 8 个样本时，留一法交叉验证 (LOOCV) 的说明。总共将训练和测试 8 个模型

 4.2.3 K-折交叉验证

        在k折交叉验证中，原始样本被随机划分为k个大小相等的子样本。在k个子样本中，保留一个子样本作为验证数据用于测试模型，剩余的k -1 个子样本用作训练数据。然后交叉验证过程重复k次，k个子样本中的每个子样本只使用一次作为验证数据。然后可以对结果进行平均以产生单个估计。这种方法相对于重复的随机子抽样的优势在于，所有样本都用于训练和验证，并且每个样本只用于验证一次。通常使用10折交叉验证，[16]但一般来说，k仍然是一个不固定的参数。

        例如，设置k = 2则是 2 折交叉验证。在 2 折交叉验证中，我们将数据集随机打乱为两个集合d 0和d 1，使两个集合大小相等（这通常通过打乱数据数组然后将其一分为二来实现）。然后我们在d 0上进行训练并在d 1上进行验证，然后在d 1上进行训练并在d 0上进行验证 。当k = n（样本次数）时，k折交叉验证等效于留一法交叉验证。[17]

        在分层 k折交叉验证中，选择分区以使平均响应值在所有分区中大致相等。在二分类的情况下，这意味着每个分区包含大致相同比例的两种类别标签。在重复的交叉验证中，数据被随机分成k个分区多次。因此，模型的性能可以在多次运行中取平均值，但这在实践中很少需要。[18]

图4 K-折交叉验证图

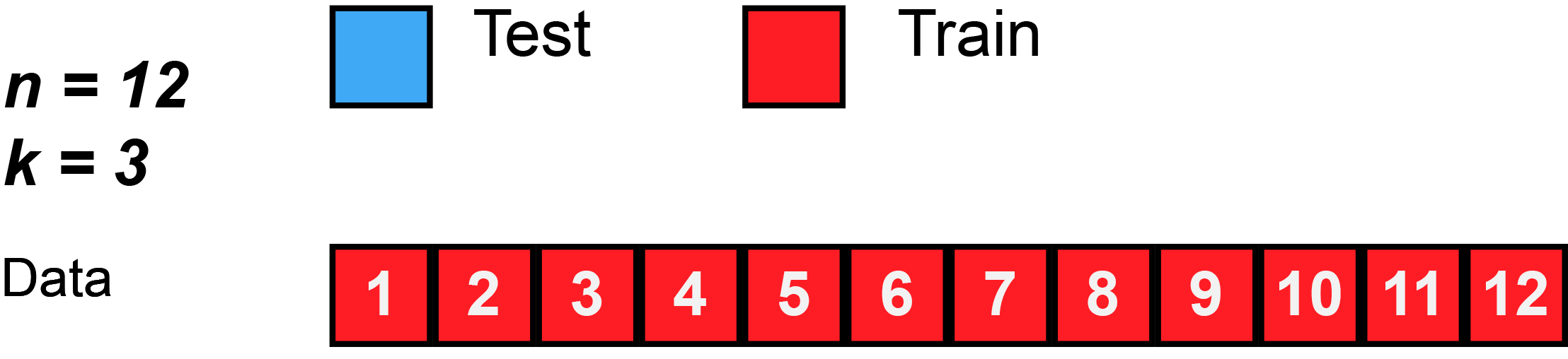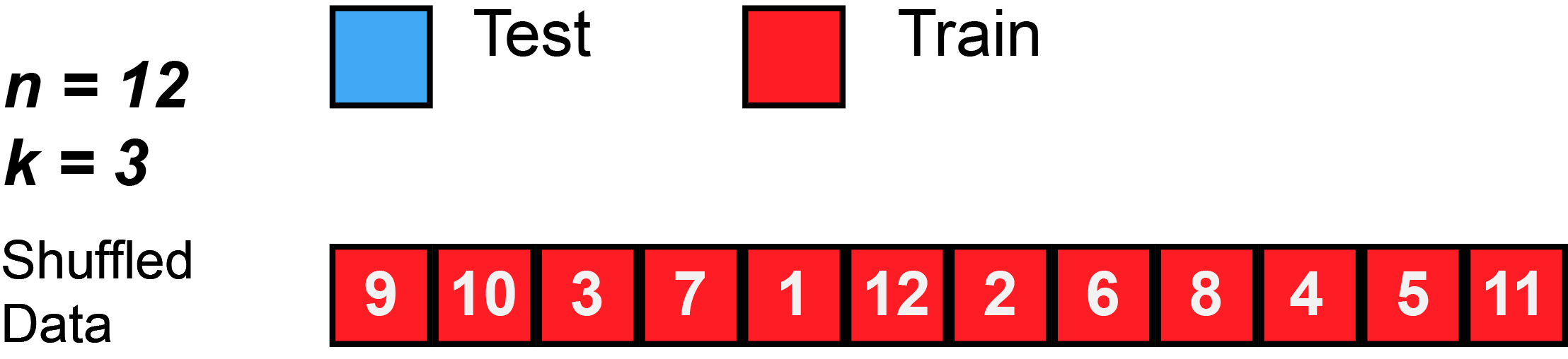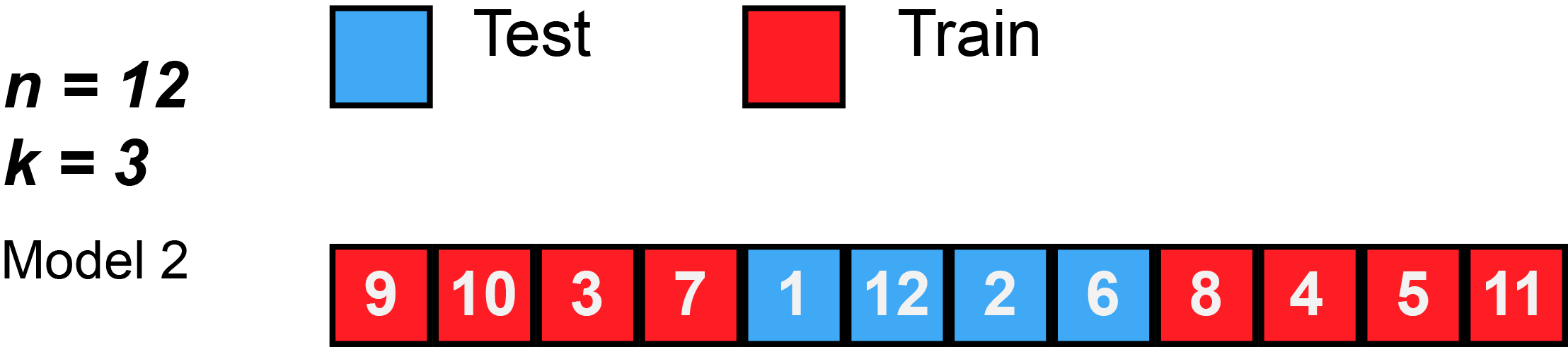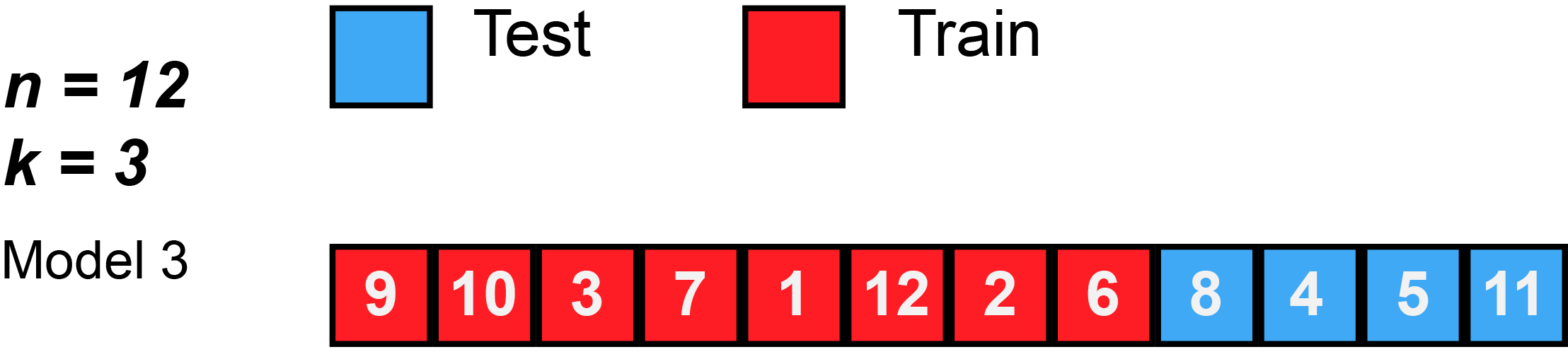
图5 当 n = 12 个观测值和 k = 3 时的 k 折交叉验证图示。数据打乱后，总共将训练和测试 3 个模型。

 4.2.3.1 重复随机子抽样验证

        这种方法，也称为蒙特卡罗交叉验证，[21]将数据集的多个随机拆分为训练和验证数据。[22]对于每个这样的拆分，模型都适合训练数据，并使用验证数据评估预测准确性。然后在拆分上平均结果。这种方法的优点（超过k折交叉验证）是训练/验证拆分的比例不依赖于迭代次数（即分区数）。这种方法的缺点是某些样本可能永远不会在验证子样本中被选择，而其他样本可能会被多次选择。换句话说，验证子集可能重叠。该方法还展示了蒙特卡罗变异，这意味着如果使用不同的随机拆分重复分析，结果会有所不同。随着随机分裂的数量接近无穷大，重复随机子抽样验证的结果趋向于留出交叉验证的结果。在这种方法的分层变体中，随机样本的生成方式使得平均响应值（即回归中的因变量）在训练和测试集中相等。如果响应是二分法且数据中两个响应值的表示不平衡，这将特别有用。一种应用重复随机子采样的方法是RANSAC。[23]

4.2.4 嵌套交叉验证

        当交叉验证同时用于选择最佳超参数集和误差估计（和泛化能力评估）时，需要嵌套交叉验证。存在许多变体。至少可以区分两种变体：

4.2.4.1 k*l 折交叉验证

        这是一个真正嵌套的变体，包含k个集合的外循环和l个集合的内循环。整个数据集被分成k个集合。一个接一个地选择一个集合作为（外）测试集，将其他k -1个集合组合成对应的外训练集。这对k个集合中的每一个重复。每个外部训练集进一步细分为l个集合。一个接一个地选择一个集合作为内部测试（验证）集，并将其他l -1 个集合组合成相应的内部训练集。这对每个l重复套。内部训练集用于拟合模型参数，而外部测试集用作验证集以提供模型拟合的无偏评估。通常，这会针对许多不同的超参数（甚至不同的模型类型）重复，并且验证集用于确定该内部训练集的最佳超参数集（和模型类型）。在此之后，使用来自内部交叉验证的最佳超参数集，在整个外部训练集上拟合一个新模型。然后使用外部测试集评估该模型的性能。

4.2.4.2 带有验证和测试集的 k 折交叉验证

        当l = k - 1时，这是一种 k*l 折交叉验证 。单个 k 折交叉验证与验证集和测试集一起使用。整个数据集被分成k个集合。一个一个地选择一个集合作为测试集。然后，一个接一个，剩余的一组作为验证集，另一个k- 2 个集合用作训练集，直到所有可能的组合都被评估。与 k*l 折交叉验证类似，训练集用于模型拟合，验证集用于每个超参数集的模型评估。最后，对于选定的参数集，使用测试集来评估具有最佳参数集的模型。在这里，可能有两种变体：要么评估在训练集上训练的模型，要么评估适合训练集和验证集组合的新模型。

4.2.4.3 拟合度量

        交叉验证的目标是估计模型与数据集的预期拟合程度，该数据集独立于用于训练模型的数据。它可用于估计适合数据和模型的任何定量拟合测量。例如，对于二分类问题，验证集中的每个案例要么被正确预测，要么被错误预测。在这种情况下，可以使用错误分类错误率来总结拟合，尽管也可以使用其他度量，如阳性预测值。当被预测的值连续分布时，均方误差、均方根误差或中值绝对偏差可以用来总结错误。

4.2.4.4 时间序列模型的交叉验证    

        由于数据的顺序很重要，交叉验证可能对时间序列模型有问题。更合适的方法是使用滚动交叉验证。[31]但是，如果性能由单个汇总统计量描述，则 Politis 和 Romano 将其描述为固定引导
[32]的方法可能会起作用。bootstrap 的统计量需要接受时间序列的一个区间，并返回关于它的汇总统计量。对固定引导程序的调用需要指定适当的平均间隔长度。

4.2.5 应用

        交叉验证可用于比较不同预测建模程序的性能。例如，假设我们对光学字符识别感兴趣，并且我们正在考虑使用支持向量机(SVM) 或k最近邻(KNN) 从手写字符的图像中预测真实字符。使用交叉验证，我们可以客观地比较这两种方法各自的错误分类字符分数。如果我们简单地根据样本内错误率比较这些方法，那么一种方法可能会表现得更好，因为它更灵活，因此更容易过度拟合与其他方法相比。

        交叉验证也可用于变量选择。[33]假设我们使用20 种蛋白质的表达水平来预测癌症患者是否会对药物产生反应。一个实际的目标是确定应该使用 20 个特征中的哪个子集来生成最佳预测模型。对于大多数建模过程，如果我们使用样本内错误率比较特征子集，则当使用所有 20 个特征时，性能最佳。然而，在交叉验证下，具有最佳拟合的模型通常只包含被认为是真正有用的特征的一个子集。

        医学统计学的最新发展是它在荟萃分析中的应用。它构成了验证统计量 Vn 的基础，Vn 用于测试荟萃分析汇总估计的统计有效性。[34] 

 4.2.6 Python代码实现K-折交叉验证数据集划分

# 导入库
from random import seed # 用于固定每次生成的随机数都是确定的（伪随机数）
from random import randrange # 用于生成随机数

def k_fold_cross_validation_split(dataset,folds=10):
    """
    该函数用于将数据集执行K-折交叉验证的划分
    Parameters
    ----------
    dataset : 二维列表
        传入需要划分交叉验证的数据集.
    folds : 整型, 可选
        传入交叉验证的折数. 默认是10.

    Returns
    -------
    basket_split_data : 三维列表
       存放的是划分好的交叉验证的数据集，三维列表里的每一个二维列表就代表了划分出的一部分样本.

    """
    # 定义一个空列表，用于存放划分好的数据集
    basket_split_data = list()
    # 计算每一折里的样本数
    fold_size = int(len(dataset)/folds)
    # 复制出一个新的数据集来做划分，从而不改变原始的数据集
    dataset_copy = list(dataset)
    # 按照需要划分的折数来循环遍历提取 
    for i in range(folds):
        # 定义一个空列表用于存放每一折里的样本数
        basket_random_fold = list()
        # 开始遍历，只要每一折里的样本数小于fold_size,就一直往里面添加数据
        while len(basket_random_fold) < fold_size:
            # 通过randrange()函数随机产生索引
            random_choose_index = randrange(len(dataset_copy))
            # 根据上面生成的随机索引将数据集中的样本加到basket_random_fold中
            basket_random_fold.append(dataset_copy.pop(random_choose_index))
        # 每一折的样本数添加好后，再将其加入到basket_split_data，此变量用于存放后续划分好的所有数据集
        basket_split_data.append(basket_random_fold)
    return basket_split_data

# 主函数
if '__main__' == __name__:
    # 定义一个随机种子，使得每次生成的随机数都是确定的（伪随机数）
    seed(1)
    dataset = [[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]]
    # 调用手动编写的k_fold_cross_validation_split函数来实现K-折交叉验证数据集的划分
    k_folds_split = k_fold_cross_validation_split(dataset,3)