ARIMA模型
arima(x,order=c(p,d,q),method=c("ML","CSS"),include.mean)
其中:
x—带估计序列;
Order—指定模型阶数;其中,P为自回归阶数;d为差分阶数,若为平稳序列,则不需要差分即d=0;q为移动平均阶数。
method—估计方法。method =CSS-ML,系统默认的是条件最小二乘估计和极大似然估计的混合方法;method =ML,极大似然估计;method =CSS,条件最小二乘估计;
include.mean—是否包含均值项,即估计结果中的intercept项。系统默认含有常数项。
补充讲解:差分的R语言
(1)P阶差分计算:p阶差分
R语言是:diff(x,differences=p)
其中:x是需要进行差分的序列;p是差分阶数,系统默认为1。
看一个例子:
x=1:10
x
[1] 1 2 3 4 5 6 7 8 9 10
y=diff(x) #对序列x进行一阶差分。
y
[1] 1 1 1 1 1 1 1 1 1
Z=diff(x,differences = 2) #对序列x进行二阶差分。
Z
[1] 0 0 0 0 0 0 0 0
(2)k步差分加入参数 lag=k
R语言是:diff(x, lag=k)
其中:x是需要进行差分的序列;k是差分步长,系统默认为1。
如计算x的3步差分,其R程序和结果为:
x=1:10
y=diff(x, lag = 3)
y
[1] 3 3 3 3 3 3 3
知识点1:ARIMA拟合
例1:对1952-1988年中国农业实际国民收入指数序列建模。
(1)读取数据
d=read.table("C:\\Users\\w\\Documents\\收入指数.txt")
#导入数据
shouru=ts(d,start=1952,end=1988,freq=1)#转化为时间序列数据
ts.plot(shouru,type=“b”) #作时序图。通过时序图,发现该序列呈现出显著的线性递增趋势,为非平稳时间序列。
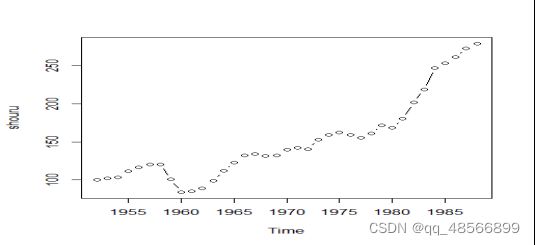
图1 国民收入指数的时序图
(2)差分运算,并对差分序列的平稳性进行判断
chafen=diff(shouru,differences=1)#对原序列进行一阶差分,剔除趋势
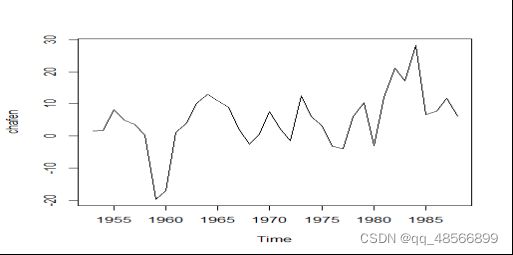
ts.plot(chafen) #时序图表明,差分后的序列在均值附近随机波动,没有明显的趋势或周期性波动,因此差分序列可能为平稳序列。
图3收入指数一阶差分序列的自相关图 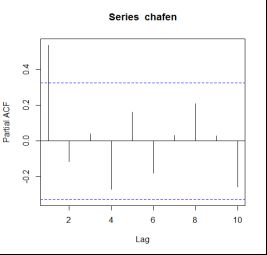
图4收入指数一阶差分序列的自相关图
acf(chafen,10) #作自相关图,发现一阶差分序列具有短期相关性,应该为平稳序列。并且可看做1阶截尾
pacf(chafen,10) #作偏自相关图,可看做拖尾
进一步的对原序列的一阶差分序列chafen进行单位根检验:
library(fBasics)
library(fUnitRoots)
#下载并安装“fUnitRoots”包(安装可以用install.packages(“fUnitRoots”)语句进行),并用library函数进行调用。该程序包中的adfTest函数可以很便捷的进行单位根检验。
for(i in 1:3)print(adfTest(chafen,lag=i,type="c"))
#对“chafen”序列进行检验类型为类型2(无趋势,有常数项),延迟阶数分别取1,2,3的单位根检验
R的运行结果如下:
Title:
Augmented Dickey-Fuller Test
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
Dickey-Fuller: -3.0057
P VALUE:
0.04732
Title:
Augmented Dickey-Fuller Test
Test Results:
PARAMETER:
Lag Order: 2
STATISTIC:
Dickey-Fuller: -2.4431
P VALUE:
0.1626
Title:
Augmented Dickey-Fuller Test
Test Results:
PARAMETER:
Lag Order: 3
STATISTIC:
Dickey-Fuller: -2.8483
P VALUE:
0.06747
ADF检验结果表明,差分序列是有常数均值的平稳序列(检验类型是“c”),且该平稳序列有1阶自相关(ADF检验P值=0.04732<0.05)。结合差分序列的时序图和自相关图,认为国民收入指数的一阶差分序列是平稳序列。
(3)差分序列的白噪声检验
Box.test(chafen, type="Ljung-Box",lag=6) #分别进行滞后期数为6和12期的纯随机性检验。这里略去12期检验的结果。
R运行结果:
data: chafen
X-squared = 15.3304, df = 6, p-value = 0.01784
当延迟阶数取6时,拒绝原假设,表明序列不是白噪声序列。
Box.test(chafen, type="Ljung-Box",lag=12)
因此差分序列为平稳非白噪声序列,可以用ARMA拟合。
(4)对平稳非白噪声的差分序列构建ARMA模型
根据ACF图和PACF图,考虑建立MA(1)模型。
arima(chafen, order = c(0,0,1),method="ML")
R运行结果:
arima(x = chafen, order = c(0, 0, 1), method = "ML")
Coefficients:
ma1 intercept
0.6710 4.9947
s.e. 0.1648 2.0139
sigma^2 estimated as 53.42: log likelihood = -122.99, aic = 251.97
(5)模型的检验
接着,对差分序列的MA(1)模型进行显著性检验:
a= arima(chafen, order = c(0,0,1),method="ML")
r=a$residuals #用r来保存残差
Box.test(r,type="Ljung-Box",lag=6,fitdf=1)
Box.test(r,type="Ljung-Box",lag=12,fitdf=1)
白噪声检验表明残差序列是一个白噪声序列,该MA(1)模型拟合差分序列是显著的。
进一步的对模型参数进行显著性检验,这里同上次课内容,此处不再赘述,结果表明参数也是显著的。
写出模型形式为:
![]()
困惑(1) :
理论上,R语句arima(chafen, order = c(0,0,1),method="ML") 和arima(shouru, order = c(0,1,1),method="ML")反映的内容是一样的。
但语句arima(shouru, order = c(0,1,1),method=“ML”) 的计算结果如下:
Call:
arima(x = shouru, order = c(0, 1, 1), method = "ML",include.mean=T)
Coefficients:
ma1
0.7355
s.e. 0.1545
sigma^2 estimated as 61.95: log likelihood = -125.74, aic = 255.49
建议:使用平稳的差分序列进行建模。
困惑(2):预测咋搞?对原序列直接建模得到的模型是有问题的,所以不能直接用R语句shouru.forecast= predict(arima(shouru, order = c(0,1,1)), n.ahead =3)进行预测,因为结果如下,是错误的结果!
shouru.forecast
$pred
Time Series:
Start = 1989
End = 1991
Frequency = 1
[1] 283.0082 283.0082 283.0082
探索解法1:使用基于差分序列构造的模型进行预测:
forecast= predict(arima(chafen, order = c(0,0,1)), n.ahead=3)
forecast
$pred
Time Series:
Start = 1989
End = 1991
Frequency = 1
[1] 5.696599 4.995631 4.995631
但得到的是差分序列的预测结果,不是我们关心的原序列的预测结果!该方法失败!
建议:各种尝试,发现和正确的预测结果最接近的唯一办法就是大家自己动手计算。
知识点2:疏系数ARIMA模型的拟合
#例2:对1917-1975年美国23岁妇女每万人生育率序列建模。
d=read.table("C:\\Users\\w\\Documents\\生育率.txt")
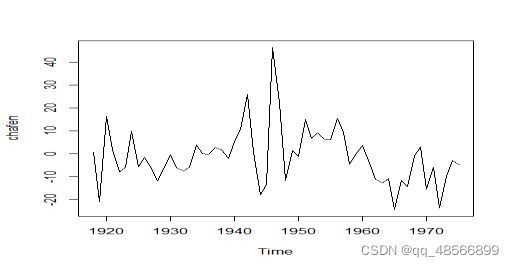
shengyu=ts(d,start=1917,end=1975,freq=1)#转化为时间序列数据ts.plot(shengyu,type="p") #作时序图。通过时序图,发现该序列为非平稳时间序列。
图1 23岁妇女每万人生育率序列的时序图
chafen=diff(shengyu,differences=1)#对原序列进行一阶差分,剔除趋势
ts.plot(chafen)#时序图表明,差分后的序列在均值附近随机波动,波动有界,没有明显的趋势或周期性波动,因此为平稳序列
图3生育率一阶差分序列的自相关图
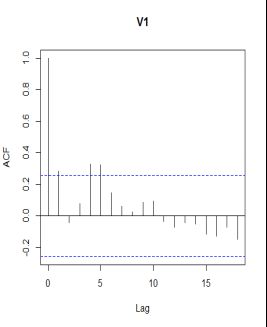
acf(chafen,18) #作自相关图,发现延迟5阶后的自相关系数都落在两倍标准差以内,序列具有短期自相关性,因此自相关图表明差分后的序列为平稳序列。且自相关系数相对而言偏向于拖尾。
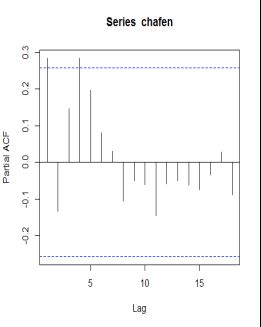
pacf(chafen,18) #作偏自相关图,发现延迟一阶和延迟四阶的偏自相关系数显著大于2倍标准差,其他阶数的偏自相关系数都较小。因此偏自相关系数1阶和4阶截尾。
Box.test(chafen, type="Ljung-Box",lag=6) #纯随机性检验
R运行结果:
data: chafen
X-squared = 20.805, df = 6, p-value = 0.001989
Box.test(chafen, type="Ljung-Box",lag=12)#序列不是白噪声序列。因此差分序列为平稳非白噪声序列,可以用ARMA拟合。结合自相关图和偏自相关图,建立疏系数模型AR(1,4)。
arima(chafen,order=c(4,0,0),fixed=c(NA,0,0,NA,NA),method="ML")
#首先尝试着构造一个非中心化(即有常数项)的AR(1,4)模型
R运行结果:
arima(x = chafen, order = c(4, 0, 0), fixed = c(NA, 0, 0, NA, NA), method = "ML")
Coefficients:
ar1 ar2 ar3 ar4 intercept
0.2537 0 0 0.3386 -1.5603
s.e. 0.1162 0 0 0.1223 3.2903
sigma^2 estimated as 117.8: log likelihood = -220.89, aic = 449.78
再尝试着构建中心化的AR(1,4)模型,并比较那个模型更优。
arima(chafen,order=c(4,0,0),fixed=c(NA,0,0,NA,0),method="ML")
R运行结果:
arima(x = chafen, order = c(4, 0, 0), fixed = c(NA, 0, 0, NA, 0), method = "ML")
Coefficients:
ar1 ar2 ar3 ar4 intercept
0.2583 0 0 0.3408 0
s.e. 0.1159 0 0 0.1225 0
sigma^2 estimated as 118.2: log likelihood = -221, aic = 448.01
所以由AIC准则,认为中心化的AR(1,4)模型更好。从而得到最终的模型形式为:![]()
接着,对该AR(1,4)模型的残差序列进行白噪声检验:
a= arima(chafen,order=c(4,0,0),fixed=c(NA,0,0,NA,0),method="ML")
r=a$residuals
Box.test(r,type="Ljung-Box",lag=6,fitdf=2)
Box.test(r,type="Ljung-Box",lag=12,fitdf=2)
结果表明,6阶和12阶延迟下的LB统计量的P值都小于显著性水平0.05,因此用AR(1,4)模型拟合差分序列得到的残差序列是一个白噪声序列,该AR(1,4)模型是显著的。
再通过参数的t检验,表明两参数都显著。参数的t检验程序如下:
(1)计算出参数的t统计量值=
,
和参数的t统计量值=
(2)求P值。参数的t检验统计量的P值的计算:
p=pt(2.2286,df=57,lower.tail = F)*2
p
[0.02980024]
注:数据有59个,估计参数2个,所以自由度为57.
同样的得到参数的t检验统计量的P值= 0.007312442。
所以参数和都显著。