线性分类器
线性分类器
在前面的课程中我们学习了逻辑回归,通过它可以把样本分为两类。
这是二维空间中的一个数据集。

如果它正好能够被一条直线分成两类,那么我们称它为线性可分数以及这条直线就是一个线性分类器。
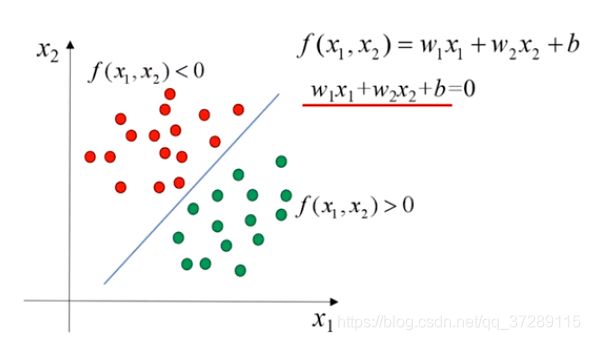
假设这是这条直线的方程 w 1 x 1 + w 2 x 2 + b = 0 w_1x_1+w_2x_2+b=0 w1x1+w2x2+b=0,那么满足这个方程的点都在这条直线上。设等号左边的表达式为 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2),那么满足 f ( x 1 , x 2 ) > 0 f(x_1,x_2)>0 f(x1,x2)>0的点都在直线的一侧,而满足 f ( x 1 , x 2 ) < 0 f(x_1,x_2)<0 f(x1,x2)<0的点都在直线的另一侧。
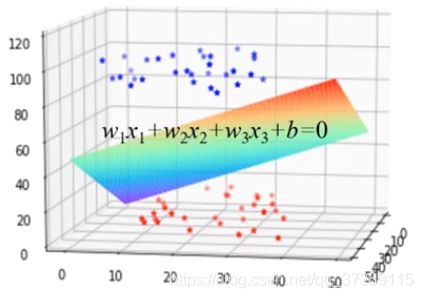
在三维空间中,如果数据集线性可分是指能够被一个平面分为两类。
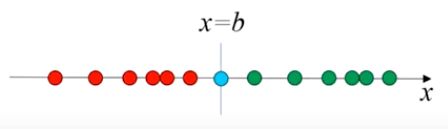
在一维空间中所有的点都在一条直线上,可以理解为他们能够被一个点分开。
这里的分类直线、平面和这个分类点被称作决策边界。
一个m维空间中的数据集,如果能够被一个超平面 W T X = 0 W^TX=0 WTX=0一分为二,那么这个数据集就是线性可分的,这个超平面就是决策边界。
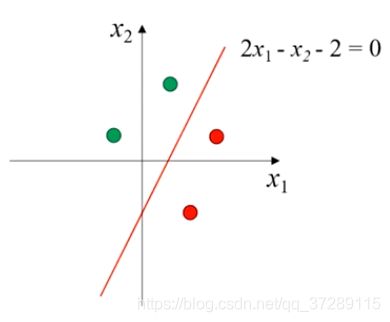
例如这是二维平面上的一条直线,它可以把平面切成两部分,也就是说将这个平面中的点分成了两类。
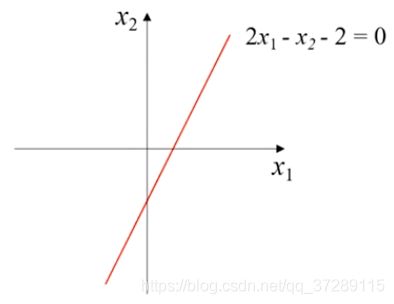
这是这个分类器的表达式 y = s t e p ( z ) = s t e p ( 2 x 1 − x 2 − 2 ) y=step(z)=step(2x_1-x_2-2) y=step(z)=step(2x1−x2−2),其中z代表线性组合 2 x 1 − x 2 − 2 2x_1-x_2-2 2x1−x2−2,step()是阶跃函数,当 a > 0 a>0 a>0,分类器的输出 y = 1 y=1 y=1,当 a < 0 a<0 a<0时, y = 0 y=0 y=0。
我们随机选取几个点
| ( x 1 , x 2 ) (x_1,x_2) (x1,x2) | z = 2 x 1 − x 2 − 2 z=2x_1-x_2-2 z=2x1−x2−2 | y y y |
|---|---|---|
| ( 1 , 3 ) (1,3) (1,3) | − 3 -3 −3 | 0 0 0 |
| ( 3 , 1 ) (3,1) (3,1) | 3 3 3 | 1 1 1 |
| ( − 1 , 1 ) (-1,1) (−1,1) | − 5 -5 −5 | 0 0 0 |
| ( 2 , − 2 ) (2,-2) (2,−2) | 4 4 4 | 1 1 1 |
当 x 1 = 1 , x 2 = 3 x_1=1,x_2=3 x1=1,x2=3时,这个点在直线的上方,这时 z = − 3 z=-3 z=−3,分类器的输出 y = 0 y=0 y=0。
当 x 1 = 3 , x 2 = 1 x_1=3,x_2=1 x1=3,x2=1时,点在直线的下方,这时 z = − 3 z=-3 z=−3,分类器的输出 y = 1 y=1 y=1。
再选择 x 1 x_1 x1和 x 2 x_2 x2分别为 ( − 1 , 1 ) (-1,1) (−1,1)和 ( 2 , − 2 ) (2,-2) (2,−2)的点,
这是点在图中的位置
这里的step()函数可以使用sigmoiid()函数代替,可以发现这就是逻辑回归。
逻辑回归其实就是构造一个线性分类器,实现对线性可分数据集的划分。其中的线性模型就是决策边界。

从这个例子中也可以,这个偏置项b的意义,如果没有这个B,那么所有的分类器都要经过原点,显然模型就丧失了一般性。
线性不可分
除了线性可分问题,还有线性不可分问题。
例如这个数据集中的两类样本点就无法通过一条直线完全区分开,它需要通过两条直线才能分开。

这个数据集中的样本,也无法通过一条直线去分开它,需要通过一条曲线分开。
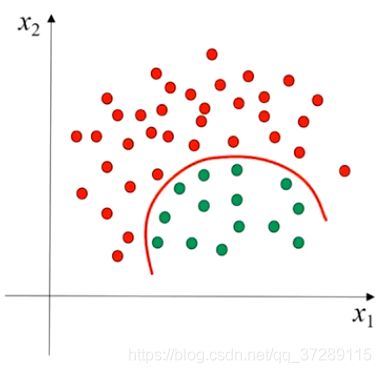
这些都是非线性可分的数据集。
在逻辑运算中与或非运算都是线性可分的。
在逻辑与运算中,只有当 x 1 x_1 x1和 x 2 x_2 x2都是1时结果才为1,否则结果为0。
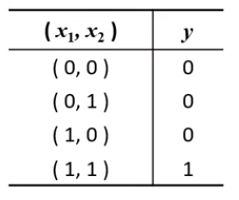
这4个点可以根据与运算的结果被分为两类。绿色的点结果为0,红色的点结果为1。

显然可以通过一条直线把这些点区分开直线的参数可以通过训练得到并且一定收敛,可以看出来,这根直线不是唯一的。这些直线也都可以区分这两类点,它们都可以作为与运算的分类器。
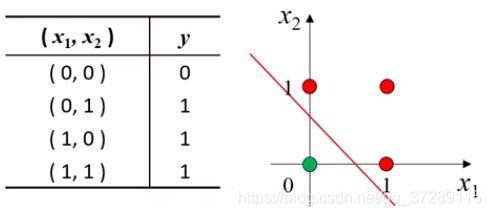
这是逻辑或运算的真值表和对应的数据点,只要 x 1 x_1 x1和 x 2 x_2 x2中有一个为1,那么结果就是1,显然他也是线性可分的。
逻辑非的输入只有一个自变量是一维的,它也是线性可分的。
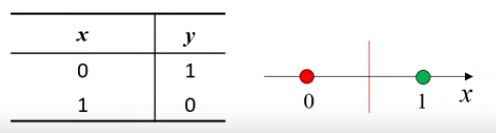
下面我们来看一下异或运算,异或是指两个操作数相同,结果为零,两个操作数不同,结果为1。异或运算也可以看作是按位加运算,0和1相加或者1和0相加,结果是1,0+0或者1+1,结果是0。
这是异或运算的4个数据点。

显然我们无法用一根直线把这两类点分开,要把它们区分开,至少需要两根直线,因此异或运算是非线性可分的。