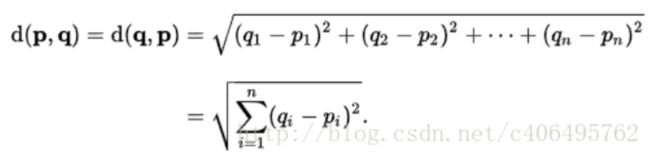机器学习实战 - k-近邻法

仅仅作为自己的学习笔记。学习内容原址：https://blog.csdn.net/c406495762/article/details/75172850

简介

• k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法 。它的工作原理是：存在一个样本数据集合，也称作为训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后，将新的数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本最相似数据(最近邻)的分类标签。一般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法中k的出处，通常k是不大于20的整数。最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

• k-近邻算法用距离度量的方法判断一个新数据所属的分类。
  

Python3代码实现

1、准备数据集

import numpy as np

'''
功能：
	创建数据集
参数：
	无
返回值：
	group - 数据集
	labels - 数据集对应的分类标签
'''
def createDataSet():
	# 四组二维特征值
	group = np.array([[1, 101], [5, 89], [108, 5], [115, 8]])
	# 四组特征对应的标签
	labels = ['爱情片', '爱情片', '动作片', '动作片']
	return group, labels

if __name__ == '__main__':
	# 创建数据集
	group, labels = createDataSet()
	# 打印数据集
	print(group)
	print(labels)

2、k-近邻算法实现

import numpy as np
import operator

'''
功能：
	实现K-临近算法——根据两点距离公式计算距离，选择距离最小的前k个点，并返回分类结果。
参数：
	inX - 用于分类的数据（测试集）
	dataSet - 用于训练的数据（训练集）
	labels - 分类标签
	k - KNN算法参数——选择距离最小的k个点
返回值：
	sortedClassCount[0][0] - 分类结果
'''
def classify0(inX, dataSet, labels, k):
	'''
	numpy.shape()函数返回一个tuple数据类型，表示数组的尺寸。
	如果为二维数组，则返回结果为：(行数， 列数)
	所以取返回结果的索引为0对应的值，即为行数，即数据集中数据的个数
	'''
	dataSetSize = dataSet.shape[0] 
	'''
	numpy.tile(A, reps)函数表示：把参数A指定的数组重复reps次。
	下面一条语句表示：
		行向量方向上重复inX共dataSetSize次(纵向), 在列向量方向上重复inX共1次(横向)
	'''
	inXMat = np.tile(inX, (dataSetSize, 1))
	# inXMat矩阵与dataSet矩阵对应位置上相减 【(x1-x2), (y1-y2)】
	diffMat = inXMat - dataSet
	# 平方 【(x1-x2)^2, (y1-y2)^2】
	sqDiffMat = diffMat ** 2
	# sum()所有元素相加; sum(axis=0)列相加; sum(axis=1)行相加 【(x1-x2)^2 + (y1-y2)^2】
	sqDistances = sqDiffMat.sum(axis=1)
	# 开方，得到距离 【((x1-x2)^2 + (y1-y2)^2)^0.5】
	distances = sqDistances ** 0.5

	'''
	numpy.argsort()函数返回从小到大排序后原来的索引位置组成的序列
	'''
	sortedDistIndices = distances.argsort()
	# 定一个记录类别次数的字典
	classCount = {}
	# 取出前k个元素的类别
	for i in range(k):
		voteIlabel = labels[sortedDistIndices[i]]
		'''
			dict.get(key, default=None)方法, 返回指定键的值, 如果值不在字典中返回默认值
			下面的语句：计算类别次数
		'''        
		classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
	'''
		sorted(key=operator.itemgetter(1)) 根据字典的值进行排序
		sorted(key=operator.itemgetter(0)) 根据字典的键进行排序
		下面的语句：根据字典的值降序排序字典中的元素
	'''
	sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
	# 返回匹配次数最多的类别, 即新数据inX的类别
	return sortedClassCount[0][0]

3、测试

import numpy as np
import cds # createDataSet()
import KNN # classify0()

if __name__ == '__main__':
    # 创建数据集
    group, labels = cds.createDataSet()
    # 测试集
    test = [101,20]
    # kNN分类
    test_class = KNN.classify0(test, group, labels, 3)
    # 打印分类结果
    print(test_class)

对上面图中红色点进行分类的结果：

• 用K-临近法进行分类其实是比较好时的。这里用时1.1s。
• 这个例子中，只有两个特征（接吻镜头、打斗镜头），所以组合成一个二维平面，对于二维平面中的两个点来说，使用两点距离公式求距离。那么对于n维特征来说呢？答案是使用 欧氏距离(也称欧几里德度量) 来求两点之间的距离：
  
• 使用K-临近法进行分类的结果是否总是正确的呢？答案是否定的，分类器并不会得到百分百正确的结果。我们可以使用多种方法检测分类器的正确率。此外分类器的性能也会受到多种因素的影响，如分类器设置和数据集等。不同的算法在不同数据集上的表现可能完全不同。通过大量的测试数据，我们可以得到分类器的错误率：分类器给出错误结果的次数除以测试执行的总数。错误率是常用的评估方法，主要用于评估分类器在某个数据集上的执行效果。完美分类器的错误率为0，最差分类器的错误率是1.0。同时，我们也不难发现，k-近邻算法没有进行数据的训练，直接使用未知的数据与已知的数据进行比较，从而得到结果。因此，可以说k-邻近算法不具有显式的学习过程。

k-近邻算法的一般流程

以上的介绍并不是完整的k-近邻算法流程。k-近邻算法的一般流程如下：

• 收集数据：可以使用爬虫进行数据的收集，也可以使用第三方提供的免费或收费的数据。一般来讲，数据放在txt文本文件中，按照一定的格式进行存储，便于解析及处理。
• 准备数据：使用Python解析、预处理数据。
• 分析数据：可以使用很多方法对数据进行分析，例如使用Matplotlib将数据可视化。
• 测试算法：计算错误率。
• 使用算法：错误率在可接受范围内，就可以运行k-近邻算法进行分类。

k-近邻算法实战 之 约会网站配对效果判定

题目背景不再赘述。

1. 收集数据

datingTestSet.txt数据下载

2. 准备数据：解析数据

在将上述特征数据输入到分类器前，必须将待处理的数据的格式改变为分类器可以接收的格式。分类器接收的数据是什么格式的？从上小结已经知道，要将数据分成两部分：特征矩阵和对应的分类标签向量。

在kNN_test02.py文件中创建名为file2matrix的函数，以此来处理输入格式问题。 将datingTestSet.txt放到与kNN_test02.py相同目录下，编写代码如下：

import numpy as np

'''
功能：
	打开并解析文件后，对数据进行分类：1代表不喜欢, 2代表魅力一般, 3代表极具魅力
参数：
	filename - 文件名
返回值：
	returnMat - 特征矩阵
	classLabelVector - 分类Label向量
'''
def file2matrix(filename):
	# 打开文件
	fr = open(filename)
	# 读取文件内容
	arrayOfLines = fr.readlines()
	# 得到文件行数
	numberOfLines = len(arrayOfLines)
	# 初始化特征矩阵：numberOfLines行，3列
	returnMat = np.zeros((numberOfLines, 3))
	# 初始化分类标签向量
	classLabelVector = []
	# 遍历文件内容，补全特征矩阵和分类标签向量
	index = 0
	for line in arrayOfLines:		
		line = line.strip() # 删除空白符(包括'\n','\r','\t',' ')
		listFromLine = line.split('\t') # 将字符串根据'\t'分隔符进行切片
		# 将数据前三列提取出来，写入returnMat中
		returnMat[index,:] = listFromLine[0:3]
		# 根据文件内容对喜欢的程度进行分类：1代表不喜欢, 2代表魅力一般, 3代表极具魅力
		# 同时将这些标签写入classLabelVector中
		if listFromLine[-1] == 'didntLike':
			classLabelVector.append(1)
		elif listFromLine[-1] == 'smallDoses':
			classLabelVector.append(2)
		elif listFromLine[-1] == 'largeDoses':
			classLabelVector.append(3)
		index += 1
	return returnMat, classLabelVector

if __name__ == '__main__':
	filename = "datingTestSet.txt"
	# 打开并处理数据
	datingDataMat, datingLabels = file2matrix(filename)
	print(datingDataMat)
	print(datingLabels)

运行效果如下：

可以看到，我们已经顺利导入数据，并对数据进行解析，格式化为分类器需要的数据格式。

接着我们需要了解数据的真正含义。可以通过友好、直观的图形化的方式观察数据。

3. 分析数据：数据可视化

在kNN_test02.py文件中编写名为showdatas的函数，用来将数据可视化。编写代码如下：

from matplotlib.font_manager import FontProperties
import matplotlib.lines as mlines
import matplotlib.pyplot as plt
import numpy as np
import OperateFile # file2matrix()

'''
功能：
	可视化数据
参数：
	datingDataMat - 特征矩阵
	datingLabels - 分类标签
返回值：
	无
'''
def showdatas(datingDataMat, datingLabels):
	# 设置汉字格式
	font = FontProperties(fname=r"C:\WINDOWS\Fonts\simsun.ttc", size=18)
	
	# 将fig画布分隔成1行1列, 不共享x轴和y轴, fig画布的大小为(13,8)
	# 当nrow=2 nclos=2时, 代表fig画布被分为四个区域(两行两列; axs[0][0]表示第一行第一个区域)
	fig, axs = plt.subplots(nrows=2, ncols=2, sharex=False, sharey=False, figsize=(13, 8))
	
	# 设置不同标签时，对应的散点图中点的颜色
	numberOfLabels = len(datingLabels)
	LabelsColors = []
	for i in datingLabels:
		if i == 1:
			LabelsColors.append('pink')
		if i == 2:
			LabelsColors.append('orange')
		if i == 3:
			LabelsColors.append('yellow')

	# 画出散点图
	# 1、以datingDataMat矩阵的第一、二列作为横纵坐标轴(散点大小为15, 透明度为0.5)
	axs[0][0].scatter(x=datingDataMat[:,0], y=datingDataMat[:,1], color=LabelsColors, s=15, alpha=.5)
	axs0_title_text = axs[0][0].set_title(u'每年获得的飞行常客里程数与玩视频游戏所消耗时间占比', FontProperties=font)
	axs0_xlabel_text = axs[0][0].set_xlabel(u'每年获得的飞行常客里程数', FontProperties=font)
	axs0_ylabel_text = axs[0][0].set_ylabel(u'玩视频游戏所消耗时间占比',FontProperties=font)
	plt.setp(axs0_title_text, size=12, weight='bold', color='black') 
	plt.setp(axs0_xlabel_text, size=9, weight='bold', color='gray') 
	plt.setp(axs0_ylabel_text, size=9, weight='bold', color='gray')
	# 2、以datingDataMat矩阵的第一、三列作为横纵坐标轴(散点大小为15, 透明度为0.5)
	axs[0][1].scatter(x=datingDataMat[:,0], y=datingDataMat[:,2], color=LabelsColors, s=15, alpha=.5)
	axs1_title_text = axs[0][1].set_title(u'每年获得的飞行常客里程数与每周消费的冰激淋公升数', FontProperties=font)
	axs1_xlabel_text = axs[0][1].set_xlabel(u'每年获得的飞行常客里程数', FontProperties=font)
	axs1_ylabel_text = axs[0][1].set_ylabel(u'每周消费的冰激淋公升数',FontProperties=font)
	plt.setp(axs1_title_text, size=12, weight='bold', color='black') 
	plt.setp(axs1_xlabel_text, size=9, weight='bold', color='gray') 
	plt.setp(axs1_ylabel_text, size=9, weight='bold', color='gray')
	# 3、以datingDataMat矩阵的第二、三列作为横纵坐标轴(散点大小为15, 透明度为0.5)
	axs[1][0].scatter(x=datingDataMat[:,1], y=datingDataMat[:,2], color=LabelsColors, s=15, alpha=.5)
	axs2_title_text = axs[1][0].set_title(u'玩视频游戏所消耗时间占比与每周消费的冰激淋公升数', FontProperties=font)
	axs2_xlabel_text = axs[1][0].set_xlabel(u'玩视频游戏所消耗时间占比', FontProperties=font)
	axs2_ylabel_text = axs[1][0].set_ylabel(u'每周消费的冰激淋公升数',FontProperties=font)
	plt.setp(axs2_title_text, size=12, weight='bold', color='black') 
	plt.setp(axs2_xlabel_text, size=9, weight='bold', color='gray') 
	plt.setp(axs2_ylabel_text, size=9, weight='bold', color='gray')
	# 4、设置图例
	didntLike = mlines.Line2D([], [], color='pink', marker='.', markersize=6, label='didntLike')
	smallDoses = mlines.Line2D([], [], color='orange', marker='.', markersize=6, label='smallDoses')
	largeDoses = mlines.Line2D([], [], color='yellow', marker='.', markersize=6, label='largeDoses')
	# 5、添加图例
	axs[0][0].legend(handles=[didntLike,smallDoses,largeDoses])
	axs[0][1].legend(handles=[didntLike,smallDoses,largeDoses])
	axs[1][0].legend(handles=[didntLike,smallDoses,largeDoses])
	# 6、显式散点图
	plt.show()

if __name__ == '__main__':
	filename = "datingTestSet.txt"
	# 打开并处理数据
	datingDataMat, datingLabels = OperateFile .file2matrix(filename)
	showdatas(datingDataMat, datingLabels)

运行效果如下：

通过图示可以很直观的发现数据的规律，比只考虑玩游戏所消耗时间占比与每年获得的飞行常客里程数时，给人的感觉就是海伦喜欢有生活质量的男人。为什么这么说呢？每年获得的飞行常客里程数表明，海伦喜欢能享受飞行常客奖励计划的男人，但是不能经常坐飞机，疲于奔波，满世界飞。同时，这个男人也要玩视频游戏，并且占一定时间比例。能到处飞，又能经常玩游戏的男人是什么样的男人？很显然，有生活质量，并且生活悠闲的人。我（原作者）的分析，仅仅是通过可视化的数据总结的个人看法，每个人的感受应该也是不尽相同。

4. 准备数据：数据归一化

给出四组样本数据：

样本	玩游戏所耗时间百分比	每年获得的飞行常用里程数	每周消费的冰淇淋公升数	样本分类
1	0.8	400	0.5	1
2	12	134000	0.9	3
3	0	20000	1.1	2
4	67	32000	0.1	2

计算样本3和样本4之间的距离：

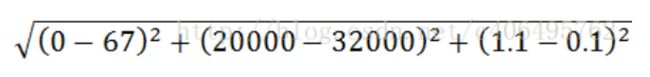
我们很容易发现，上面方程中数字差值最大的属性对计算结果的影响最大，也就是说，每年获取的飞行常客里程数对于计算结果的影响将远远大于其他两个特征——玩视频游戏所耗时间占比和每周消费冰淇淋公斤数的影响。

产生这种现象仅仅是因为飞行常客里程数这一特征值总是远大于其他特征值。但海伦认为这三种特征是同等重要的，因此作为三个等权重的特征之一，飞行常客里程数并不应该如此严重地影响到计算结果。

在处理这种不同取值范围的特征值时，我们通常采用的方法是 将数值归一化。如，将取值范围处理为０到１或者-１到１之间。下面的公式可以将任意取值范围的特征值转化为０到１区间内的值：

$newValue=(oldValue-min)/(max-min)$

其中min和max分别是数据集某一特征中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂度，但为了得到准确结果，我们必须这样做。

编写名为autoNorm的函数，用来将数据归一化。代码如下：

import numpy as np
'''
功能：
	归一化数据
参数：
	dataSet - 特征矩阵
返回值：
	normDataSet - 归一化后的特征矩阵
	ranges - 数据范围
	minVals - 数据最小值
'''
def autoNorm(dataSet):
	# 获得每个特征里对应的最小特征值和最大特征值
	minVals = dataSet.min(0)
	maxVals = dataSet.max(0)
	# 最大值和最小值差值
	ranges = maxVals - minVals
	# 创建一个与特征矩阵dataSet行列数一样的空矩阵，用来存放归一化的特征矩阵
	normDataSet = np.zeros(np.shape(dataSet))
	# 得到矩阵的行数
	m = dataSet.shape[0]
	'''
	numpy.tile(A, reps)函数表示：把参数A指定的数组重复reps次。
	下面一条语句表示：
		行向量方向上重复minVals共m次(纵向), 在列向量方向上重复minVals共1次(横向)
		然后另原始值减去最小值
	'''
	normDataSet = dataSet - np.tile(minVals, (m, 1))
	# 再除以最大、最小值的差, 得到归一化数据
	normDataSet = normDataSet / np.tile(ranges, (m, 1))
	return normDataSet, ranges, minVals

主函数：

import OperateFile # file2matrix()
import HandleData # autoNorm()

if __name__ == '__main__':
	filename = "datingTestSet.txt"
	# 打开并处理数据
	datingDataMat, datingLabels = OperateFile.file2matrix(filename)
	# 数据归一化
	normDataSet, ranges, minVals = HandleData.autoNorm(datingDataMat)
	print(normDataSet)
	print(ranges)
	print(minVals)

运行结果：

可以看到，我们已经顺利将数据归一化了。

5. 测试算法：验证分类器

机器学习算法一个很重要的工作就是评估算法的正确率，通常我们只提供已有数据的90%作为训练样本来训练分类器，而使用其余的10%数据去测试分类器，检测分类器的正确率。需要注意的是，10%的测试数据应该是随机选择的（这种“随机选择”其实是需要遵循一定的理论基础的，只不过这里就不再讲解了，《西瓜书》里有看到相关内容）。

创建函数datingClassTest()：

import OperateFile # file2matrix()
import HandleData # autoNorm()
import KNN # classify0()

'''
功能：
	测试算法，并计算出正确率
参数：
	无
返回值：
	无
'''
def datingClassTest():
	filename = "datingTestSet.txt"
	# 打开并处理文件中的数据
	datingDataMat, datingLabels = OperateFile.file2matrix(filename)
	# 数据归一化
	normMat, ranges, minVals = HandleData .autoNorm(datingDataMat)

	# 获得normMat的行数
	m = normMat.shape[0]
	# 取所有数据的10%
	hoRatio = 0.10
	# 计算10%的测试数据的个数
	numTestVecs = int(m * hoRatio)

	# 统计使用该算法进行分类时分类错误的次数
	errorCount = 0.0
	# 前numTestVecs个数据作为测试集（其余numTestVecs ~ m之间的数据作为训练集）
	for i in range(numTestVecs):
		classifierResult = KNN.classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 4)
		print("分类结果：%d\t真实类别：%d" % (classifierResult, datingLabels[i]))
		if classifierResult != datingLabels[i]:
			errorCount += 1.0
	print("错误率：%f%%" % ((errorCount / float(numTestVecs)) * 100))

if __name__ == '__main__':
	HandleData.datingClassTest()

运行结果：

我的错误率算出来和原博主的不同啊，为什么？？？程序都一样。。。数据有所改变？不可能啊。。。额，我不要纠结这些细枝末节了！

我们可以改变函数datingClassTest()内变量hoRatio和分类器k的值，检测错误率是否随着变量值的变化而增加。依赖于分类算法、数据集和程序设置，分类器的输出结果可能有很大的不同。

6. 应用算法：构建完整可用系统

写一个小程序：输入约会网站上目标对象的信息，程序会给出她对男方喜欢程度的预测值。

创建函数classifyPerson()，代码如下：

import numpy as np
import OperateFile # file2matrix()
import HandleData # autoNorm()
import KNN # classify0()

'''
功能：
	输入约会网站上目标对象的信息，程序会给出她对男方喜欢程度的预测值。
参数：
	无
返回值：
	无
'''
def classifyPerson():
	# 保存可能的结果
	resultList = ['讨厌', '有些喜欢', '非常喜欢']
	# 输入三维特征
	precentTats = float(input("玩视频游戏所耗时间百分比: "))
	ffMiles = float(input("每年获得的飞行常客里程数: "))
	iceCream = float(input("每周消费的冰激淋公升数: "))

	filename = "datingTestSet.txt"
	# 打开并处理文件中的数据
	datingDataMat, datingLabels = OperateFile.file2matrix(filename)
	# 数据归一化
	normMat, ranges, minVals = HandleData.autoNorm(datingDataMat)

	# 生成测试集
	inArr = np.array([precentTats, ffMiles, iceCream])
	# 测试集归一化
	norminArr = (inArr - minVals) / ranges
    # 得到分类结果
	classifierResult = KNN.classify0(norminArr, normMat, datingLabels, 3)
    # 打印结果
	print("你可能%s这个人！" % (resultList[classifierResult-1]))


if __name__ == '__main__':
	ApplyPerson.classifyPerson()

运行结果：

k-近邻算法实战 之 sklearn手写数字识别

对于需要识别的数字，假定已经使用图形处理软件处理成具有相同的色彩和大小、宽高为32像素x32像素。但是为了方便理解，我们将图片转换为文本（尽管采用本文格式存储图像不能有效地利用内存空间）。数字的文本格式如下图所示：

与此同时，这些文本格式存储的数字的文件命名也很有特点，格式为：数字的值_该数字的样本序号，如下所示。

实战使用的数据集：https://github.com/Jack-Cherish/Machine-Learning/tree/master/kNN/3.%E6%95%B0%E5%AD%97%E8%AF%86%E5%88%AB

这里不再讲解用Python写k-邻域分类器的方法，因为这不是本小节的重点。接下来，我们将使用强大的第三方Python科学计算库Sklearn构建手写数字系统。

Sklearn简介

Scikit learn 也简称sklearn，是机器学习领域当中最知名的python模块之一。sklearn包含了很多机器学习的方式：

• Classification 分类
• Regression 回归
• Clustering 非监督分类
• Dimensionality reduction 数据降维
• Model Selection 模型选择
• Preprocessing 数据与处理

使用sklearn可以很方便地让我们实现一个机器学习算法。一个复杂度算法的实现，使用sklearn可能只需要调用几行API即可。所以学习sklearn，可以有效减少我们特定任务的实现周期。

Sklearn安装

自行解决。

Sklearn实现k-近邻算法

sklearn.neighbors模块实现了k-近邻算法（官网：https://scikit-learn.org/stable/modules/classes.html#module-sklearn.neighbors）。

这个模块下的KNeighborsClassifier即为k-近邻算法（官网：https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier）：

KNneighborsClassifier的八个参数说明（对官网中的说明进行的翻译）：

• n_neighbors：默认为5，就是k-NN的k的值，选取最近的k个点。
• weights：默认是uniform，参数可以是uniform、distance，也可以是用户自己定义的函数。uniform是均等的权重，就说所有的邻近点的权重都是相等的。distance是不均等的权重，距离近的点比距离远的点的影响大。用户自定义的函数，接收距离的数组，返回一组维数相同的权重。
• algorithm：快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。
• leaf_size：默认是30，这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度，同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
• metric：用于距离度量，默认度量是minkowski，也就是p=2的欧氏距离(欧几里德度量)。
• p：距离度量公式。在上小结，我们使用欧氏距离公式进行距离度量。除此之外，还有其他的度量方法，例如曼哈顿距离。这个参数默认为2，也就是默认使用欧式距离公式进行距离度量。也可以设置为1，使用曼哈顿距离公式进行距离度量。
• metric_params：距离公式的其他关键参数，这个可以不管，使用默认的None即可。
• n_jobs：并行处理设置。默认为1，临近点搜索并行工作数。如果为-1，那么CPU的所有cores都用于并行工作。

KNeighborsClassifier提供了以一些方法供我们使用：

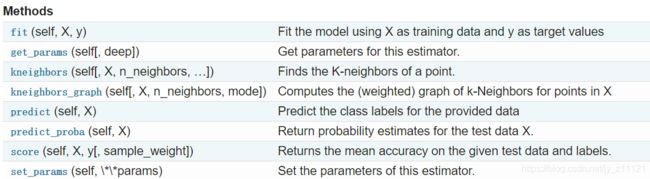
具体用法请查看官网手册。下面直接讲手写数字识别系统的实现。

Sklearn小试牛刀

我们知道数字图片是32x32的二进制图像，为了方便计算，我们可以将32x32的二进制图像转换为1x1024的向量。对于sklearn的KNeighborsClassifier输入可以是矩阵，不用一定转换为向量，不过为了跟自己写的k-近邻算法分类器对应上，这里也做了向量化处理。然后构建kNN分类器，利用分类器做预测。创建kNN_test04.py文件，编写代码如下：

import numpy as np
import operator
from os import listdir
from sklearn.neighbors import KNeighborsClassifier as kNN


'''
功能：
	将32x32的二进制图像转换为1x1024向量。
参数：
	filename - 文件名
返回值：
	returnVect - 返回的二进制图像的1x1024向量
'''
def img2vector(filename):
	returnVect = np.zeros((1, 1024))
	fr = open(filename)
	# 按行读取（共32行）
	for i in range(32):
		lineStr = fr.readline()
		# 把一行中的32个元素添加到returnVect中
		for j in range(32):
			returnVect[0, 32*i + j] = int(lineStr[j])
	return returnVect


'''
功能：
	手写数字分类测试
参数：
	无
返回值：
	无
'''
def handwritingClassTest():
	# 得到trainingDigits目录下的所有文件名
	trainingFileList = listdir('trainingDigits')
	# 得到trainingDigits目录下文件个数
	m = len(trainingFileList)
	# 初始化训练集的特征矩阵
	trainingMat = np.zeros((m, 1024))

	# 初始化训练集的Labels
	hwLabels = []

	# 从文件名中解析出训练集的类别
	for i in range(m):
		# 获得文件名
		fileNameStr = trainingFileList[i]
		# 获得分类的数字
		classNumber = int(fileNameStr.split('_')[0])
		# 将获得的类别添加到hwLabels中
		hwLabels.append(classNumber)
		# 将每一个文件内的1x1024数据存储到trainingMat矩阵中
		trainingMat[i,:] = img2vector('trainingDigits/%s' % (fileNameStr))

	# 构建KNN分类器
	neigh = kNN(n_neighbors = 3, algorithm = 'auto')
	# 拟合模型：trainingMat为训练集的特征矩阵, hwLabels为对应的标签
	neigh.fit(trainingMat, hwLabels)
	# 错误结果计数
	errorCount = 0.0

	# 得到测试集
	testFileList = listdir('testDigits')
	mTest = len(testFileList)
	for i in range(mTest):
		fileNameStr = testFileList[i]
		classNumber = int(fileNameStr.split('_')[0])
		vectorUnderTest = img2vector('testDigits/%s' % (fileNameStr))
		# 获得预测结果
		classifierResult = neigh.predict(vectorUnderTest)
		print("分类返回结果为%d\t真实结果为%d" % (classifierResult, classNumber))
		if (classifierResult != classNumber):
			errorCount += 1.0
	print("总共错了%d个数据\n错误率为%f%%" % (errorCount, errorCount/mTest * 100))


if __name__ == '__main__':
	handwritingClassTest()

运行结果：

上述代码使用的algorithm参数是auto，更改algorithm参数为brute，使用暴力搜索，你会发现，运行时间变长了，变为10s+。更改n_neighbors参数，你会发现，不同的值，检测精度也是不同的。自己可以尝试更改这些参数的设置，加深对其函数的理解。

实例-用Sklearn再实现约会网站

import numpy as np
import operator
from os import listdir
from sklearn.neighbors import KNeighborsClassifier as kNN
import OperateFile

if __name__ == '__main__':
	filename = "datingTestSet.txt"
	# 打开并处理文件中的数据
	datingDataMat, datingLabels = OperateFile.file2matrix(filename)
	
	# 构建KNN分类器
	neigh = kNN(n_neighbors = 4, algorithm = 'auto', p=3)
	# 拟合模型
	neigh.fit(datingDataMat, datingLabels)
	
	# 取出测试集
	m = len(datingDataMat)
	# 取所有数据的10%
	hoRatio = 0.10
	# 计算10%的测试数据的个数
	numTestVecs = int(m * hoRatio)

	errorCount = 0.0

	# 前numTestVecs个数据作为测试集（其余numTestVecs ~ m之间的数据作为训练集）
	for i in range(numTestVecs):
		classifierResult = neigh.predict([datingDataMat[i, :]])
		print("分类结果：%d\t真实类别：%d" % (classifierResult, datingLabels[i]))
		if classifierResult != datingLabels[i]:
			errorCount += 1.0
	print("错误率：%f%%" % ((errorCount / float(numTestVecs)) * 100))

运行结果：

总结

kNN算法的优缺点

优点

• 简单好用，容易理解，精度高，理论成熟，既可以用来做分类也可以用来做回归；
• 可用于数值型数据和离散型数据；
• 训练时间复杂度为O(n)；无数据输入假定；
• 对异常值不敏感。

缺点

• 计算复杂性高；空间复杂性高；
• 样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）；
• 一般数值很大的时候不用这个，计算量太大。但是单个样本又不能太少，否则容易发生误分。
• 最大的缺点是无法给出数据的内在含义。

其他

• 关于algorithm参数kd_tree的原理，可以查看《统计学方法 李航》书中的讲解；
• 关于距离度量的方法还有切比雪夫距离、马氏距离、巴氏距离等。