【成长笔记】逻辑回归与正则化

ng的第三周课程讲的内容十分丰富，可花了我不少时间来消化。嗯，开局先抛出一个问题哈，譬如，如何根据已有的邮件数据（贴上了垃圾邮件与非垃圾邮件的标记），来判断未来的一封邮件是否是垃圾邮件呢？ 

以上的问题本质上是一个分类问题，而且是一个二元分类，通俗讲就是非此即彼。假设我们标记垃圾邮件为0，标记非垃圾邮件为1，邮件的一些特征我们也进行数值化，利用我们之前了解的特征缩放等将数据整理。那么，我们需要的是一个适合的算法，对原始数据训练出一个模型。这样，新的邮件数据，我们带入这个模型，根据返回的值，比如1，我们就可以判断其为非垃圾邮件了。

所以啊，该用什么方法来对数据们进行分类呢？在我们的日常中，我们是如何对事物进行分类的呢？应该大体是这样子的，了解了事物之后，发现他们之间的不同点，根据他们的不同点来分类不同事物。

那么，开动脑洞，在数学上，我们是不是可以想象两类数据泾渭分明，会存在这么一条线将他们分割开来，一边是“0”，一边是“1”，这样子，不就分开了吗？

哈哈，脑洞大开，逻辑并不严谨，闲话不多说，让我们带着问题去思考吧，Let's go!

---------------我是萌萌的分割线------------------

Logistic Regression（逻辑回归）是一个受到广泛传播与应用的分类算法。这个算法的表达式是这样子的：

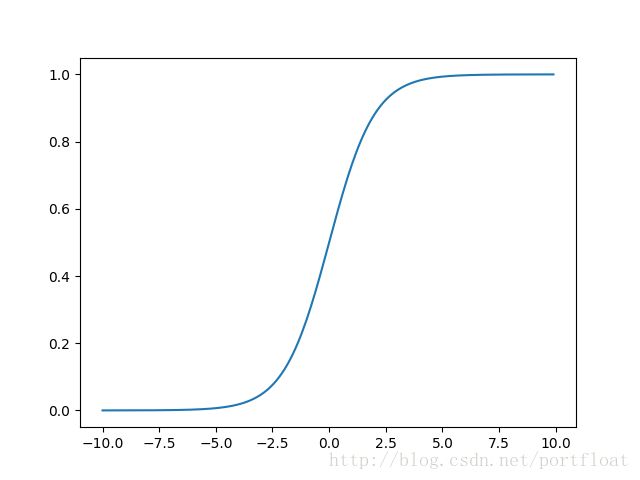
这个函数表达式被称为logistic function，也经常被称为sigmoid function。当  , 则 ,那么  ;当  , 则 ,那么 b ;当  ,  ;当  ,  。嗯，这个函数长这个样子的：

发现了不，这个函数的值域为(0,1)，而且分布很均匀，任何一个数据值投入到函数中的x中，都可以映射到(0,1)，那么，我们可以将他们的值分为两类，当y>0.5时（即x>0），就属于“1”，当y<0.5时（即x<0），就属于“0”。

所以啊，结合之前我们学过的知识，对于二分类问题，我们可否利用逻辑回归对他们进行分类呢？

我们需要对原有的逻辑回归函数稍稍改造一下，如下哦：

此时，我们再令  。

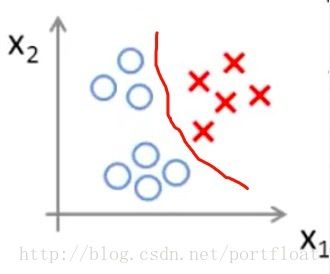
在这里，就要提出一个新的概念了，Decision Boundary（决策边界），什么是决策边界呢？还记得前文脑洞大开的时候，想象有这么一条线可以将两类数据集分割开来吗？一端是属于“1”，一端是属于“0”。结合这个逻辑回归函数，我们是不是发现了什么呢？

嘿嘿，没错，这个  中的  其实就是这么一条线啦，所以，知道我们为什么要对它进行改造了吧，因为很多时候，这么一条线不可能是一条直线的，  能够适应更多的可能。嗯，这么说你可能难以理解的话，请看下面这几个图：

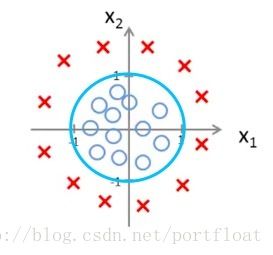
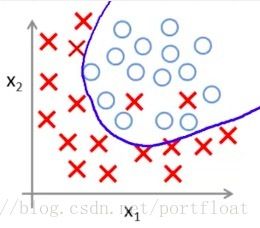
嗯，我们需要找到一条分割开圆和叉的线，什么线比较好呢？接着看哦：

嗯，完美，在这个圆圈之外属于叉，圆圈之内属于圆。那么这个边界呢？我们该怎么去定义呢？假设 ，当  (省略号全是0)，此时 。 这个式子 让你想到了什么呢？或者说是 ，这是一个半径为1，圆心在原点的圆。没错，就是上图中那个分开两类图形的分界线。所以，我们简单分析下，当  ，即  ,当  ，即  。回顾我们前文的假设：当y>0.5时（即x>0），就属于“1”，当y<0.5时（即x<0），就属于“0”。所以，结合上图，我们相当于将圆圈外的叉标记为“1”，将圆圈内的圆标记为“0”。而通过逻辑回归得到的值，我们可以将它看成是分类为“1”的概率，通过逻辑回归，则我们很轻易地将两类数据分类了。当然，关键是我们得找到他们之间的决策边界，上面这个例子的决策边界就是那个圆啊。

以上的例子是个比较简单的例子，对于更多更加复杂的分类，本质上我们都能找到一个不错的决策边界，不知道大家是否了解泰勒多项式，理论上，任何函数都可以用泰勒多项式进行拟合，而泰勒多项式也可以由  表示，所以，简单如上图中的决策边界，复杂如五角星或者我们一时看不出来的决策边界，都可以拟合出一个多项式函数。当我们找到了这个决策边界后，再利用logistic对之进行分类，就可以对两类数据集进行比较好的分类了。

所以，你有没有这么一个疑惑呢？生活中并非所有的问题都是非此即彼的问题啊，二分类毕竟是少数，大多时候，我们面临的是one-vs-all(一对多)的问题，那么，我们要分类的不仅仅是两种，而是多种。可是逻辑回归只能分出两类，如果我有三类，四类，十类甚至更多需要分类，那该怎么办呢？

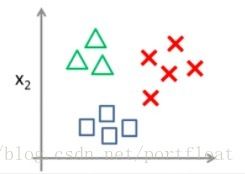
别着急，接着看，咱们也可以静下来好好思考下。先别考虑10类甚至更多的，考虑最简单的多类——3类，如图：

对于这么三类（三角形，矩形，叉），该怎么分类呢？两两比较嘛？那另外一个咋办呢？嗯，别掉入牛角尖哦，看全局试试。我干嘛不这样比较呢？选中其中一类，其他的无论多少类，我都当作另一类，多简单哈。同理，对于每一类都这么想，就如下图：

那么，我们标记三角形，矩形，叉分别0，1，2。则，此时，y = {0,1,2}，那么，对于以上的三个分类，我们可以对它进行分类概率的计算：

所以，我们可以比较这三个值，哪个值最大，就意味这它属于当前那一类的概率最大。那么，三类也可以推而广之，如果有n类，那么就是在这基础上。

这样，多类分类的情况也就解决了。

所以，又回到了在前几篇文章中需要解决的问题了，  该怎么获得呢？还是利用梯度下降法，我们要获得其代价函数J，在前面的线性回归中，我们的代价函数是这样子的：

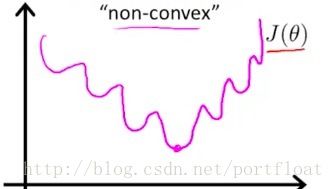
那么对于逻辑回归的代价函数可以这样吗？嗯，最好别这样，因为如果依然使用线性回归的代价函数，会导致梯度下降很难到达全局最优点，可能会得到局部优点，如图：

所以，换一个代价函数的表示：

我们可以将它变为一个式子：

为什么这么写稍稍分析下应该就了然了，这儿就不再具体分析了。找到了代价函数J，其余的过程就和之前是一样的。

不断的repeat以下过程：

当然，此时的  。

嗯，以上的问题清晰后，接下来我们要学习一个很重要的概念，regularization（正则化）,这是什么呢？别急，慢慢来说明。

前文我们说了分类中，找到了决策边界，就可以利用逻辑回归进行分类了，那么，自然的，我们该选择什么决策边界好呢？由前文我们也可以看出，决策边界取决于  。我们看看以下三种决策边界（g是logistic function）：

它的决策边界是：   。

它的决策边界是：  。

它的决策边界是：  。

这里面哪个拟合得最好呢？当然是第三个了，几乎把所有的都完美区分开了，我们看看它的函数十分复杂，特征比另外两个都多。但是，第三个真的是最佳的吗？不是的。

这里再引入一个新概念：Overfitting（过拟合）。什么是过拟合呢？一个高阶多项式可能很好地拟合训练集，能够几乎拟合所有的训练数据，但这函数太过庞大，变量太多，如果没有足够多的数据去约束这个变量过多的模型，就是过拟合。通俗地讲，过拟合就是在训练集（已知数据）上表现非常好，但是对于未知的数据表现得非常糟糕。嗯，再通俗地讲，比如在图片识别中，识别大熊猫，正常特征是黑眼圈等，结果，对于已有数据，它把一些大熊猫的特征也算进去了，譬如耳朵上要有什么图案啊才是大熊猫，结果这么一来，对于训练的大熊猫图片当然可以非常好地表现，给一张新的大熊猫图片，它耳朵上没有那个图案，结果就被错误分类了。所以过拟合就是，训练集好，预测集糟糕。

所以啊，我们就得防止过拟合，如图二那样的，就表现得不错，图一拟合的不好，那叫欠拟合，解释啥的自己查哦，这儿不详细解释。

所以，如何防止过拟合呢？

1. 减少特征，比如上图第二个，就比第三个少很多特征，函数表现上就简单多了。

2. 正则化。

因为有的时候我们不知道减少什么特征比较好，以及我们也不希望减特征，特征越多，越能使得训练表现好嘛。正则化可以在不减少特征的情况上，保持一个好的表现。

怎么做到的呢？

简单地说，就是在代价函数后面加一个小尾巴惩罚项，比如在线性回归函数中：

 ，其中  称为惩罚项系数。小尾巴前面那项是我们原本的代价函数，现在加上了惩罚项后，我们要使得代价函数最小，则后面的小尾巴也必须要小，小尾巴小的话，那么  就不能太大，如果  很小的话，那么那个  所在的项就接近于0了，也就可以近似地看成没有了那个特征。

接下来进行梯度下降，不断地迭代以下过程。至于逻辑回归的惩罚项，这儿就不再详细展开了，可以思考下哦～

当然了，正则化还不仅仅只有这么一个作用呢。还记得前面学过的正规方程法吗？它有一个很大的缺陷，就是如果矩阵是奇异矩阵的话，那么就不能使用了。

而加上个正则项后，那就是非奇艺的了，正规方程法就可以很好地使用了。

以上。

--------------我是萌萌的分割线-----------------

ng的课程越来越走近深水区了，不过发现英文字幕比中文字幕更加利于理解，ng的英语里并没有多少难词，把基本的术语了解了，看英文字幕对于理解会更加有帮助，因为中文翻译的不是非常准确。

哈哈，总算写完了，准备待会儿洗漱下就睡了，晚安～