【机器学习】深入浅出经典贝叶斯统计
贝叶斯统计
概率的类型
假设 为 数据对象的值 , 的相关频率为 ,其中N表示总的出现次数().
一个事件 的概率为 ,代表事件 发生的可能性有多大。
我们通过在 范围内为某个空间中的结果(事件)集分配一个数值概率来构造一个概率空间。
当结果是一个不确定但可重复的过程的结果时,概率总是可以通过简单地观察多次过程的重复并计算每个事件发生的频率来衡量。这些频率概率可以很好地陈述客观现实。如
电子自旋是1/2。
希格斯粒子的质量在124到126 GeV之间。
现在宇宙中暗能量的比例在68%到70%之间。
超导体Hg-1223的临界温度超过130K。
如果我们假设这些是通用的常数,而这些常数不会因为你需要测量过程而得到不同的结果。这决定了我们最感兴趣的陈述不能被赋予频率统计的概率。
然而,如果我们也允许概率来衡量在陈述中的主观的"信仰程度",那么就可以使用概率论的完整机制来讨论更有趣的陈述。这些被称为贝叶斯概率。
贝叶斯概率是由贝叶斯理论所提供的一种对概率的解释,它采用将概率定义为某人对一个命题信任的程度的概念。
最传统的概率理论是基于事件的相对频率(频率),而贝叶斯观点更加灵活地看待概率。在任何情况下,概率总是介于0和1之间,所有可能事件的概率值的总和等于1。
贝叶斯概率和频率概率相对,它从确定的分布中观测到的频率或者在样本空间中的比例来导出概率。粗略描述两种概率统计是:
频率统计: 无趣陈述的客观概率。
贝叶斯统计: 有趣陈述的主观概率。
贝叶斯联合概率
离散随机变量的联合分布
对离散随机变量而言,联合分布概率质量函数为 ,即
因为是概率分布函数,所以必须有
连续随机变量的联合分布
类似地,对连续随机变量而言,联合分布概率密度函数为 ,其中 和 分别代表 时 的条件分布以及 时 的条件分布; 和 分别代表和的边缘分布。
同样地,因为是概率分布函数,所以必须有
独立变量的联合分布
对于两相互独立的事件 及 ,任意x和y而言有离散随机变量 ,或者有连续随机变量 。
贝叶斯统计从联合概率分布开始
括号内分别是数据特征 ,模型参数 和超参数 。 上的下标是为了提醒我们,通常所使用的参数集依赖于超参数(例如,增加n_components为新组件添加参数)。有时我们将这个 对称为模型。
这个联合概率意味着模型参数和超参数都是随机变量,这意味着它们标记了潜在概率空间中的可能结果。
可能性
可能性 是模型参数 (给定超参数 )和数据特征 的函数,度量模型给定的观测数据的概率(密度)。例如,高斯混合模型有如下可能性函数:
参数 为:
及超参数 。注意,对于任何(固定)参数和超参数的值,可能性必须在数据上进行标准化。而不是在参数或超参数上标准化的。
可能性度函数在频率统计和贝叶斯统计中都起着核心作用,但是他们使用和解释的方式不同,这里主要讨论贝叶斯的观点,其中 和 是随机变量,可能性函数与条件概率相关。
条件概率的表示在给定模型 的情况下,观察特征 。
贝叶斯定理
贝叶斯定理是概率论中的一个定理,描述在已知一些条件下,某事件的发生概率。
比如,如果已知某人妈妈得癌症与寿命有关,使用贝叶斯定理则可以通过得知某人年龄,来更加准确地计算出他妈妈罹患癌症的概率。
通常,事件A在事件B已发生的条件下发生的概率,与事件B在事件A已发生的条件下发生的概率是不一样的。然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式的一个用途,即透过已知的三个概率而推出第四个概率。贝叶斯定理跟随机变量的条件概率以及边际概率分布有关。
我们将可能性与条件概率联系起来,我们就可以应用概率演算的早期规则(2 & 3)来推导广义贝叶斯规则:
上面的每一项都有一个名称,测量不同的概率:
后验概率: 是给定数据 和超参数 的参数值 的条件概率。
可能性: 是给出模型 的数据 的概率,又称为模型 的似然。
先验概率: 是给定超参数的模型参数的概率,并且在所有可能的数据上被边缘化。
证据: 是给出超参数的数据的概率,并且在给出超参数的所有可能的参数值上被边缘化。
在典型的推理问题中,(1)后验概率是我们真正关心的,而(2)似然是我们知道如何计算的。(3)先验概率是我们必须量化我们对宇宙不同可能的主观"信仰程度"。
(4)证据呢?利用前面的概率计算法则,我们发现(4)可以由(2)和(3)计算出来:
这个结果并不稀奇,因为分母必须将比率标准化,以产生可能性。
当参数值集为离散时,即 ,, 时,归一化积分转换为一个求和:
上面的广义贝叶斯定理假设任何超参数的值都是固定的,因为 在所有4项中,但一个完整的推论还要求我们考虑不同的超参数设置,而这个更难的模型选择问题待后续分享。
从案例中理解贝叶斯定理

问题:
假设你在某次会议上第一次见到某人,他穿着印有England的T恤。通过以下方法估计他是英国人的可能性:
定义数据 和模型 ,为了简单起见,假设没有超参数。
分配相关的可能性和先验概率(如以上(2)和(3))。
计算上述广义贝叶斯定理结果。
解决方案:
将数据 定义为观察到的人穿着印有
England字样的T恤。定义模型有单个参数,人的国籍 ,.
我们不需要对所有可能的数据指定一个完整的可能性函数,因为我们只有一个单一的数据。相反,分配可能性概率就足够了:
分配会议参与者的先验概率:
我们现在可以计算:
注意,我们计算证据 时使用的是和而不是积,因为 是离散的。
你可能分配了不同的概率,因为这些是理性的人可能不同意的主观评估。然而,通过允许一些主观性,我们能够在一些(主观的)假设下做出精确的陈述。
注意,可能性概率的总和不是1,因为可能性是在数据上归一化的,而不是在模型上归一化的,不像先验概率的总和是1。
这样一个简单的例子可以在联合概率 , 的二维空间中图形化表示:
广义贝叶斯定理可以看作是一种学习规则,当有新信息时更新我们的知识:

图中隐含的时间线衍生出了后验和先验概率等术语,尽管没有要求先验是基于“新”数据之前收集的数据。
即使贝叶斯推理问题听起来很简单,但可能很难做对,所以在推理之前,清楚地说明你知道什么或假设什么,以及你希望学习什么是很重要的,下面是总结了贝叶斯推理问题的主要步骤:
列出可能的模型,也就是你的假设。
给每个模型分配一个先验概率。
定义每个模型的每个可能观察的可能性 。
应用贝叶斯定理从新的数据中学习并更新之前的数据。
用python函数实现贝叶斯定理
对于可能的模型和观测数量有限的问题,所需的计算是简单的算术计算问题,但当模型和观测数量越来越多,所需的计算将会越来越复杂。借助于Python函数可以简化算术,并专注于逻辑推理。
自定义函数实现
将贝叶斯定理封装为自定义函数learn:
def learn(prior, likelihood, D):
# 计算每个模型的贝叶斯定理分子。
prob = {M: prior[M] * likelihood(D, M) for M in prior}
# 计算贝叶斯定理分母。
norm = sum(prob.values())
# 返回每个模型的后验概率。
return {M: prob[M] / norm for M in prob}上面的问题变成:
prior = {'English': 0.2, '!English': 0.8}
def likelihood(D, M):
if M == 'English':
return 0.4 if D == 't-shirt' else 0.6
else:
return 0.1 if D == 't-shirt' else 0.9
learn(prior, likelihood, D='t-shirt'){'English': 0.5, '!English': 0.5}一个学习更新的(后)输出可以是下一个更新的(前)输入。例如,如果一个人第二天还穿着印有England的T恤,我们该如何更新我们的知识?
post1 = learn(prior, likelihood, 't-shirt')
post2 = learn(post1, likelihood, 't-shirt')
# 输出post1为第二次的输入
print(post2){'English': 0.8, '!English': 0.2}python模块实现
mls包有一个函数Learn是用来计算以上问题的,并且允许用一个调用进行多个更新,并将学习过程记录为pandas表输出:
from mls import Learn
Learn(prior, likelihood, 't-shirt', 't-shirt')| English | !English | |
|---|---|---|
| PRIOR | 0.2 | 0.8 |
| D=t-shirt | 0.5 | 0.5 |
| D=t-shirt | 0.8 | 0.2 |
典型的角色扮演游戏骰子
 来源https://commons.wikimedia.org/wiki/File:Dice_(typical_role_playing_game_dice).jpg
来源https://commons.wikimedia.org/wiki/File:Dice_(typical_role_playing_game_dice).jpg
假设
有人掷出个骰子,点数分别是6、4、5,却不告诉你它是4、6、8、12还是20个面的骰子。
问题
你的直觉是基于滚动的真实边线数是多少?
识别问题中的模型(假设)和数据。
定义你的先验假设每个模型都是等可能的。
定义一个可能性函数,假设每个骰子都是公平的。
使用
Learn函数来估计后验概率,为每一次滚动的边数。
解答
我们可以确定骰子不是4面的(因为滚动 > 4),并猜测它不太可能是12或20面的(因为最大的滚动是6)。
这个问题中的模型对应骰子的面数:4、6、8、12、20。
这个问题中的数据是掷骰子的结果:6、4、5。
定义每个模型等可能的先验假设:
prior = {4: 0.2, 6: 0.2, 8: 0.2,
12: 0.2, 20: 0.2}假设每个骰子都是均匀的,定:
def likelihood(D, M):
if D <= M:
return 1.0 / M
else:
return 0.0最后,将所有细节放在一起,估计每个模型在每次滚动后的后验概率:
Learn(prior, likelihood, 6, 4, 5)| 4 | 6 | 8 | 12 | 20 | |
|---|---|---|---|---|---|
| PRIOR | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| D=6 | 0 | 0.392 | 0.294 | 0.196 | 0.118 |
| D=4 | 0 | 0.526 | 0.296 | 0.131 | 0.047 |
| D=5 | 0 | 0.635 | 0.268 | 0.079 | 0.017 |
有点出乎意料的是这个骰子问题有实际的应用和历史意义!
想象一个工厂生产了 的产品,每个产品的序列号是1 - 。如果你随机选择物品并查看它们的序号,那么估算 的问题就类似于我们的骰子问题,但需要考虑更多模型。这种方法在二战中被盟军成功地用于估算德国坦克的生产速度[2] ,当时大多数学术统计学家都拒绝使用贝叶斯方法。
要了解更多关于贝叶斯方法发展的历史观点(以及发展过程中的许多障碍),请阅读The Theory That Would Not Die[3]《不会消亡的理论》这本有趣的书。
注意
虽然上面的离散例子可以精确地解出来,但一般情况下这个结果并不正确。更具挑战是当计算连续随机变量时,在贝叶斯定理分母中 )作为边缘化积分来求解:
通过选择适合的先验概率函数和可能性函数,这个积分可以通过解析来执行求解。然而,对于大多数实际工作来说,需要用近似的数值方法来计算复杂的分布。这类常用的方法有马尔可夫链蒙特卡罗和变分推理。
先验信息选择问题
优先权的选择必然是主观的,有时还会引起争议。尽管如此,这里总结了如下一般准则:
从信息性实验中得出的数据推论对你的先验选择不是很敏感。
如果你的(后验)结果对你选择的先验是敏感的,此时你需要更多(或更好的)数据。
对于先验 ,我们使用beta分布[4],它由超参数 和 指定:
其中 是Gamma函数[5]与阶乘 相关的。
该函数提供了一个二项式过程的先验(或后验),对应于先前(或更新)的测量值,该二项式共有 次过程,并在这些试验中,有 次通过, 次不通过。
下面定义函数binomial_learn函数计算并绘制先验概率、可能性及后验概率曲线。
def binomial_learn(prior_a, prior_b, n_obs, n_pass):
"""
prior_a, prior_b: 超参数a和b
n_obs:观察或测量次数
n_pass:通过样本数
"""
theta = np.linspace(0, 1, 100)
# 计算和绘制关于theta的先验概率。
prior = scipy.stats.beta(prior_a, prior_b)
plt.fill_between(theta, prior.pdf(theta), alpha=0.25)
plt.plot(theta, prior.pdf(theta), label='Prior')
# 计算并绘制给定任意theta的固定数据的可能性。
likelihood = scipy.stats.binom.pmf(n_pass, n_obs, theta)
plt.plot(theta, likelihood, 'k:', label='Likelihood')
# 根据观测数据计算并绘制后验曲线。
posterior = scipy.stats.beta(prior_a + n_pass, prior_b + n_obs - n_pass)
plt.fill_between(theta, posterior.pdf(theta), alpha=0.25)
plt.plot(theta, posterior.pdf(theta), label='Posterior')
plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=3,
ncol=3, mode="expand", borderaxespad=0., fontsize='large')
plt.ylim(0, None)
plt.xlim(theta[0], theta[-1])
plt.xlabel('Pass fraction $\\theta$')通过图形实例回答如下问题
Q1: 在你的研究领域想一个问题,这个问题适用于这个推理问题。
Q2: 使用超参数 ,从2个观测中推断 。
根据观察数据解释为什么后验是合理的。
什么值 是绝对排除的数据?这有意义吗?
这三个量是如何标绘的?
Q3: 用 代替 ,从相同的2次观察中推断 。
根据观察数据,后验仍然合理吗?解释你的推理。
你如何在这两种主观的先验中做出选择?
Q4: 使用上面的每个先验均不同的数据: 100个试验中有60个通过。
先验和可能性的相对重要性如何随着更好的数据而变化?
为什么现在的可能性值这么小?
binomial_learn(prior_a=1, prior_b=1, n_obs=2, n_pass=1)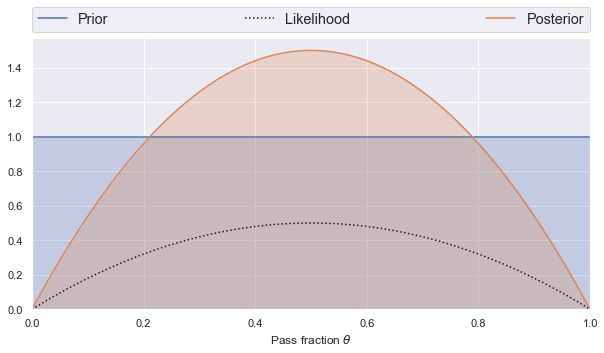
后验概率峰值是在观察到的平均通过率为1/2处。这显然是合理的,因为我们只做了两个观察。
绝对排除0和1,因为我们已经观察到1个通过和1个不通过。
先验概率、后验概率及可能性是标准化的 ,所以它们在图中的面积是1。而因所有可能的数据的可能性也都是标准化的,所以他们在这个图中面积没有1。
binomial_learn(5, 10, 2, 1)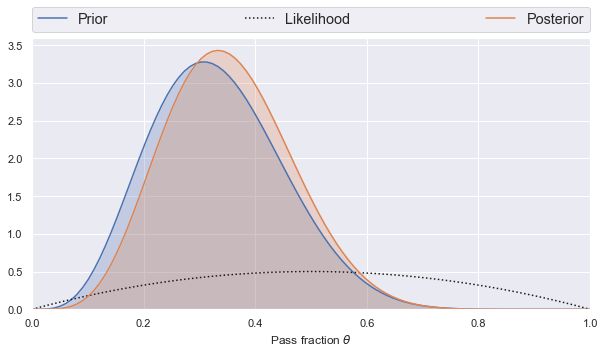
当用 代替 后,
后验概率的峰值在远离平均观察通过率的1/2处。如果继续相信先验信息,这也是合理的,因为在相对于没有任何信息的数据中,贝叶斯定理告诉我们,它应该占据我们对 的知识。
另一方面,如果我们不能证明为什么这个先验比之前的平坦分布的先验更加可信,那么我们必须得出这样的结论: 的值是未知的,这些数据也是没有任何帮助的。如果在之前的13次【】实验中观察到4次【】通过,那么新的先验概率是非常合理的。然而,如果从未观察到这个过程,并且没有理论偏见,那么原来的平坦分布的先验是合理的。
接下来增加观察次数,即增加数据量。
binomial_learn(1, 1, 100, 60)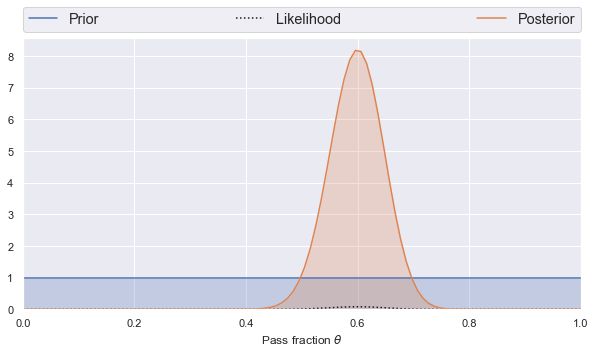
binomial_learn(5, 10, 100, 60)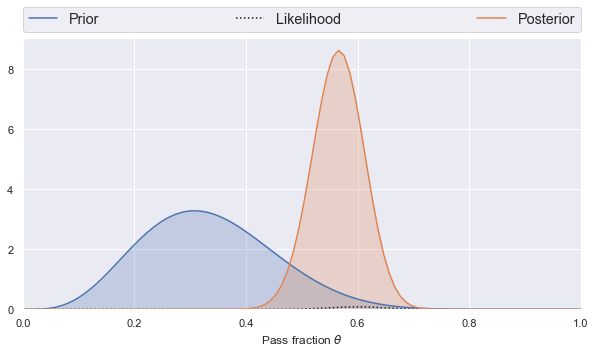
数据越多,先验的影响就越小。
且可能性值更大,因为有更多的可能结果(通过或不通过)与更多的观测值,所以任何一个结果变得相对不太可能。
贝叶斯网络
贝叶斯网络(Bayesian network),又称信念网络(belief network)或是有向无环图模型(directed acyclic graphical model),是一种概率图型模型,借由有向无环图(directed acyclic graphs, or DAGs)中得知一组随机变量 及其 组条件概率分布的性质。
举例而言,贝叶斯网络可用来表示疾病和其相关症状间的概率关系;倘若已知某种症状下,贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。
一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,它们可以是可观察到的变量,抑或是隐变量、未知参数等。
连接两个节点的箭头代表此两个随机变量是具有因果关系或是非条件独立的;而两个节点间若没有箭头相互连接一起的情况就称其随机变量彼此间为条件独立。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(descendants or children)”,两节点就会产生一个条件概率值。
贝叶斯网络是用于建模属性和类别标签之间的概率关系。通过建立概率论和图伦的概念,贝叶斯网络能够捕获更简单的条件独立形式,使用简单的示意进行表示。他们还提供了必要的计算结构,以有效的方式对随机变量执行推断。
概率图模型
贝叶斯网络术语捕获随机变量之间的概率关系的模型,被称为概率图模型(probabilistic graphical model)。这些模型背后的基本概念是使用图表示,其中图的节点对应于随机变量,节点之间的边缘表示概率关系。
我们从贝叶斯联合概率开始:
当一个函数有数据特征 ,模型参数 和超参数 ,这个函数通常是一个非常高维的函数。
在最普遍的情况下,联合概率需要大量的数据来估计。然而,许多问题可以用联合概率(通过假设一些随机变量是相互独立的)来(近似)描述。
概率图模型是随机变量之间假定的直接依赖关系的一种方便的可视化方法。
例如,假设我们有两个参数 ,并且没有超参数,那么联合概率 可以利用概率演算的规则,以不同的方式展开成条件的乘积:
或者
对应的图表为:
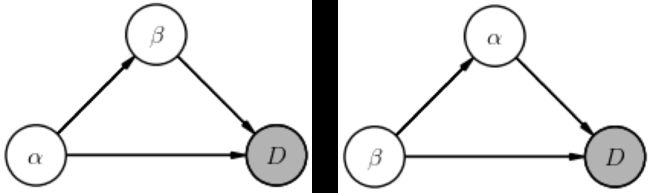
读这些图的方法是:一个标记为 的节点表示联合概率中的(乘性)因子 ,其中 列出了其他节点的箭头指向该节点(以任何顺序,根据概率微积分规则1)。阴影节点表示直接观察到的随机变量(即数据),而非阴影节点表示(未观察到的)潜在随机变量。
这些图都描述了具有两个参数的联合概率。建立具有任意参数的联合概率的规则为:
选择参数(任意)的顺序。
第一个参数的节点箭头指向所有其他节点(包括数据)。
第n个参数的节点箭头指向所有后面的参数节点和数据。
有了 参数,就有 可能的图,潜在依赖关系的数量随着 迅速增长。
为了减轻这种阶乘增长,我们寻找不互相依赖的随机变量对。例如,在两个参数的情况下:

请注意每个图是如何描述一个不同的故事的。例如,第一个图告诉我们,只知道 就可以预测数据,但是我们对 的先验知识依赖于 。因此,实际上,简化联合概率涉及到绘制一个图表,为数据和模型讲述一个合适的故事。
从案例中理解贝叶斯网络
考虑观察某人扔一个球,并测量它落地的距离,以推断重力的强度:
数据是测量范围 。
参数是球的初始速度 和角度 以及重力的强度 。
超参数是球的直径 和风速 。
画一个图例来说明这个推断的联合概率
假设投掷者总是尽可能地用力投掷,然后根据风向调整角度。画一个图来表示这个简单的联合概率中的直接依赖关系。
写出对这个推理问题感兴趣的后验。
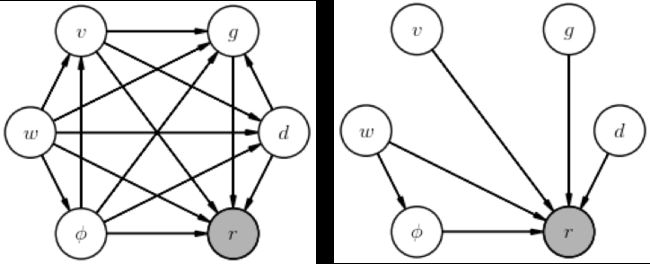
我们对这个推论最感兴趣的后验是
但更完整的后验为
这两个式子的不同之处在于,在第一种情况中,我们忽略了"讨厌的"参数 。
这些图中的箭头定义了条件依赖关系的方向。它们通常反映了潜在物理系统的因果影响,具有有向边的概率图被称为贝叶斯网络。
也可以在没有指定方向的情况下,绘制对称连接节点的图。这些被称为马尔可夫随机场或马尔可夫网络,当依赖关系在两个方向或一个未知方向流动时适用。你可以阅读更多相关信息马尔可夫网络[6].
贝叶斯网络的特点
给定属性和类别标签之间的概率关系,贝叶斯网络提供了表示图模型的方法。
贝叶斯网络可以轻松处理相关或冗余属性的存在。
贝叶斯网络对不包含类别标签对判别信息的不相关属性具有鲁棒性。
贝叶斯网络由于表示复杂形式的关系的能力,更加容易过拟合,因此需要更多的训练实例来有效地学习概率表。
参考资料
[1]
贝叶斯统计: https://github.com/dkirkby/MachineLearningStatistics
[2]估算德国坦克的生产速度: https://en.wikipedia.org/wiki/German_tank_problem
[3]The Theory That Would Not Die: https://www.amazon.com/Theory-That-Would-Not-Die/dp/0300188226
[4]beta分布: https://en.wikipedia.org/wiki/Beta_distribution
[5]Gamma函数: https://en.wikipedia.org/wiki/Gamma_function
[6]马尔可夫网络: https://en.wikipedia.org/wiki/Markov_random_field

往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载黄海广老师《机器学习课程》视频课黄海广老师《机器学习课程》711页完整版课件本站qq群554839127,加入微信群请扫码: