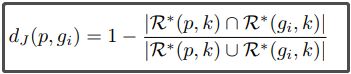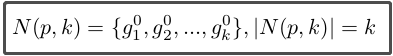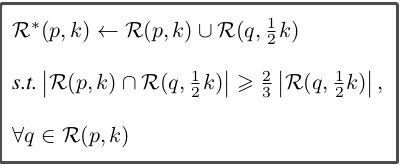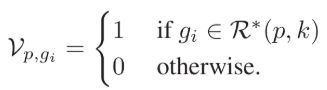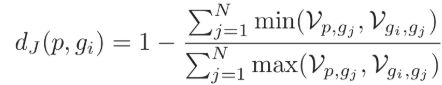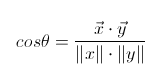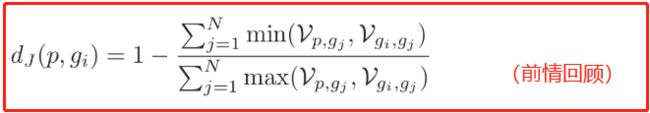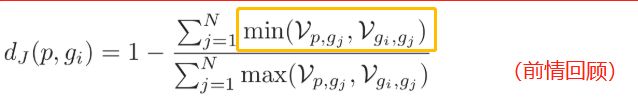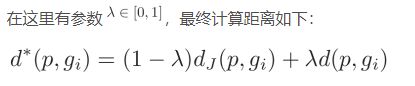详细解读行人重识别的k-reciprocal Encoding(k个相互近邻编码方法) re-ranking方法及其实现代码解读
建议读者手中有re-ranking的代码,或者看过某个行人充实别的代码。
一,re-ranking大致流程:
re-ranking是一个图像检索问题,给定一个probe,要从图片集gallery中找出与它相似的图片。如:
既然是检索问题,那么ranking前得到的ranking list就很重要,ranking list有没有使用某些算法得到,这有着很大区别,如下图:
L是没有用算法的ranking list,可以看到AP只有9.05%,准确率非常低,而用了算法的ranking list则可以达到51.98%。所以可以说 re-ranking 是高度依赖ranking list 的质量的。
那之前获取ranking list的算法有哪些呢?
这里主要叫一个 k-nearest neighbors (k近邻)算法。顾名思义,就是从gallery中选择与probe最相似的前k个嘛。
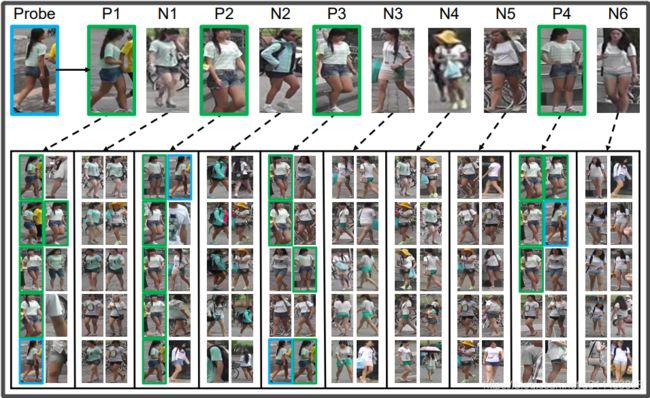
按理来说 ,这种方法应该效果挺好的,但实验中证明,获得k近邻时,很有可能有false match的噪音数据参杂进这个ranking list中,如下图:
其中P1,P2,P3,P4都为true match,但却没有全在比较前的位置,false match中的N1,N2却排到了一个比较靠前的位置,因此就引出了今天要讲的算法 k-reciprocal nearest neighbor(k相互近邻)算法。
二,k-reciprocal nearest neighbor 算法
这个算法的思路就是:如果两张图片A,B相似,那么B应该会在A的前K个近邻里面,反过来,A也会在B的前K个近邻里面。但如果两张图C,D不相似,即使C在D的前K个近邻里面,D也不会在C的前K个近邻里面。如下图:
那么这个k-reciprocal nearest neighbor算法主要的过程是怎么实现呢?
假设我们有一个图片probe p,和图片集gallery g:
我们首先要计算 p 和所有 g 中的图片的马氏距离 和 杰卡德距离(jaccard distance)。
其中马氏距离用于获得 initial ranking list,杰卡德距离用于获得 k-reciprocal 的 ranking list。
马氏距离好理解,它可以看作是忽略了量纲的欧式距离。
(马氏距离与欧式距离,余弦距离的关系可看这个博客:https://blog.csdn.net/u014453898/article/details/98657357)
而杰卡德距离就要稍微讲一下了:
2.1杰卡德(jaccard)距离是什么?
杰卡德(jaccard)距离的公式是:
其中R,R星,p,k是什么呢,我们一一来看:
gi 为 gallery集中的图片。p为probe。
R是符合 k-reciprocal nearest neighbors 的图片集合,注意它是一个集合,可以定义为:(而R星只是做了扩展的R,等下会说)
这里又出现了N,那我们看看,既然R是符合k相互近邻的图片集合,那N就是K近邻的图片集合嘛,N定义如下:
(|N(p,k)|表示N中候选图片的数目)
那么到这里,我们看回R的定义公式就可以很清楚地看到,R(p,k)是以p作为probe,在gallery图片集中,能与p能有k相互近邻的图片集合。
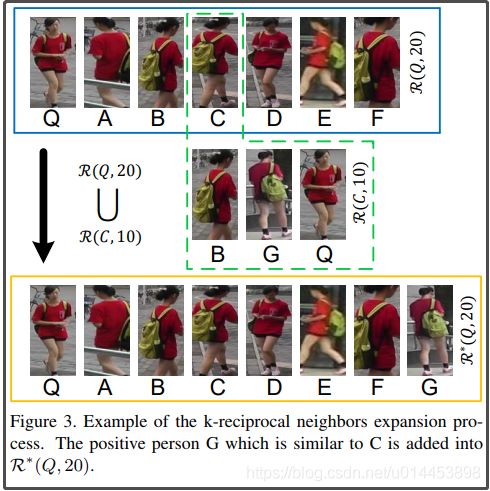
根据前面的描述,k-reciprocal nearest neighbors(K相互近邻)比k-nearest neighbors(K近邻) 和probe p更相关。然而,由于照明、姿态、视图和遮挡的变化,正样本图像可能被从k-nearest neighbors中排除,并且随后不被包括在k-reciprocal nearest neighbors中。为了解决这个问题,我们根据以下条件将R(p,k)中每个候选项的1/2 k-reciprocal nearest neighbors增量地添加到更鲁棒的集合R*(p,k)中:
稍微通俗讲一下,这个R星的形成公式:
我们已经知道R(p,k)是一个集合,里面全是gallery中符合p的k-reciprocal nearest neighbors(K相互近邻)的图片gi。
然后我们现在要做的就是遍历这些gi,每一个拿出来就是q,然后我们再用这个q作为新的probe,在gallery图片集里做k变成原来一半的k-reciprocal nearest neighbors 得到R(q,1/2k),若R(p,k)和R(q,1/2k)的交集中的图片数大于等于2/3乘R(q,1/2k)中的图片数目的话,就把R(p,k)和R(q,1/2k)的并集作为R星(p,k)。
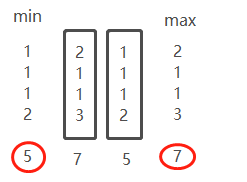
下面用一个比较距离的例子来呈现R星的形成:
首先Q作为probe,蓝色框即为Q的k-reciprocal nearest neighbors(K相互近邻)集R(Q,20),R(Q,20)中的C单独拿出来作为q,同时K减一半,即K = 20/2 = 10,所以第二行即为R(C,10),R(Q,20)与R(C,10)的的并集(即相同的图片)数为2,而R(C,10)的个数为3。 2/3 乘 3 = 2 ,符合![]() ,R星(Q,20)就为R(Q,20)与R(C,10)的交集。(第三行)。
,R星(Q,20)就为R(Q,20)与R(C,10)的交集。(第三行)。
知道R星是什么,就不难看懂杰卡德(jaccard)距离了:
改造杰卡德(jaccard)距离
然而,这样的杰卡德(jaccard)距离还是有缺点的:
1.取交集和并集的操作非常耗时间,尤其是在需要计算所有图像对的情况下。一个可选方式是将近邻集编码为一个等价的但是更简单的向量,以减少计算复杂度。
2.这种距离计算方法将所有的近邻样本都认为是同等重要的,而实际上,距离更接近于probe的更可能是正样本。因此,根据原始的距离将大的权值分配给较近的样本这一做法是合理的。
3.为了得到鲁棒的距离度量,结合原始距离和Jaccard距离是有必要的。
为了克服上述缺点,我们开始改造Jaccard距离。首先,将k-reciprocal nearest neighbors(缩写k-rnn)集合编码为N维的二值向量![]() =
=![]() ,其中每个元素由以下指示函数定义:
,其中每个元素由以下指示函数定义:
接着,为了给每一个元素根据原始距离来重新分配权值,我们采用了高斯核。于是将向量改写为: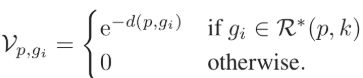
于是,计算Jaccard距离时用到的交集和并集的基数就改写为: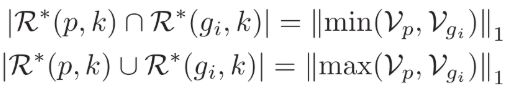
最后,我们终于得到了改造过的Jaccard距离:
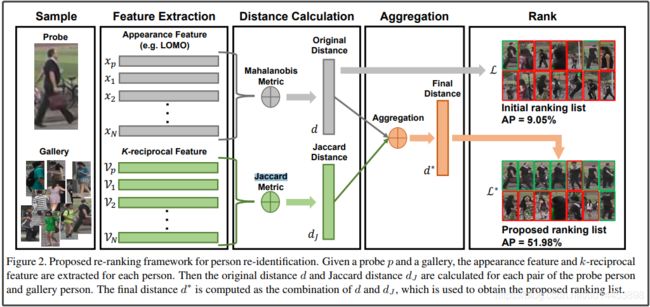
2.2 k-reciprocal nearest neighbor 算法与马氏距离和杰卡德距离
从上图可以看出,在Feature Extraction(特征提取)阶段,灰色的是提取probe p和gallery中每张图片各自的外观特征(这用需要做re ranking的神经网络来完成),绿色的是提取probe p与gallery中每张图片的K-reciprocal特征V,公式是上述的Vp,g公式。灰色特征形成马氏距离后,就可以作为原始距离(intial distance),绿色则作为杰卡德(jaccard)距离,然后两个距离聚合在一起就成了最终距离(final distance),final distance可以用于最终的ranking list。到这整个流程就完成了。
距离聚合公式:(入是自己手动设置的)
三,代码讲解部分
3.1 在输入re-ranking代码前,作的一些预处理
首先用到的网络(用于提取图片外观特征的网络)是Mutiple Granularity Network(MGN),数据集是Market-1501。
在讲re-ranking代码之前,先说说MGN,MGN是把每张图片都处理成一个(1x2048)的向量来代替原来的图片。
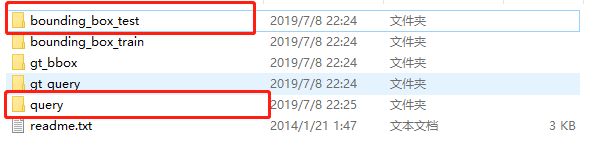
re-ranking部分用到数据集Market-1501的两个文件夹如下图:
bounding_box_test作为gallery图片集,一共19733张,但是里面有些图片id是-1的,MGN舍弃了这部分,所以真正读入的图片为15914张。所以gallery的图片数就是15914。
query则是作为probe,只不过里面有很多个probe,一共3369张。
在进入re-ranking代码前:
预处理先对 query 和 gallery 进行特征提取,注意这里不是一张张提取,而是整个集合的图片一起提取特征,所以输出的是一个大矩阵。
用MGN提取query的特征,由于一张图片会转换成1x2048的向量,所以拥有3369张图片的query的特征就是3369x2048的矩阵。(用qf表示这个矩阵)
同理用MGN提取gallery的特征,得到15914x2048的矩阵。(用gf表示这个矩阵)
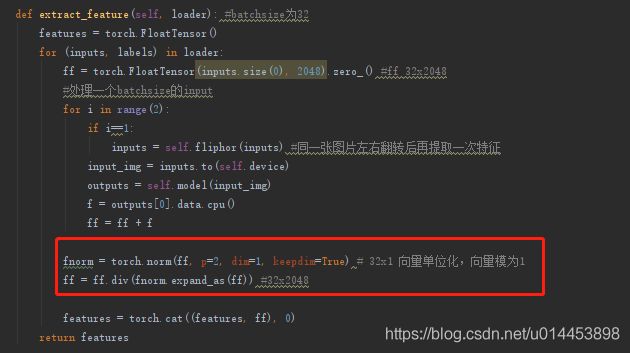
特征提取的代码如下:
大家只要关注红框处就行,红框处给每个表示图片的向量做了向量的单位化!!!这个很重要!单位化后的向量的模就为1。
这个很重要的原因是,提取了qf和gf之后,就开始算马氏距离了,但是代码不是用马氏距离的公式来算马氏距离,而是使用了一个小技巧,用余弦距离来算马氏距离,为什么可以这样子呢,参考链接:https://blog.csdn.net/u014453898/article/details/98657357
余弦距离为:
当两向量的模为1时,向量相乘的积就是它们的余弦距离。并且MGN在读入数据集时,就应该做过标准化了,因此数据的均值为0,标准差为1,这种情况下,马氏距离又等于欧式距离,余弦距离与欧式距离有转换公式,所以马氏距离可以用余弦距离表示:
![]()
因此可以通过qf和gf两个矩阵相乘得到两个矩阵的余弦距离:
上面四条代码:
q_g_dist 表示:qf 和 gf的余弦距离。维度3369x15914,表示3329张probe和各自15914张gallery的余弦距离。
q_q_dist 表示:qf自己的余弦距离。维度为3369x3369,表示每张probe 和 其他probe的余弦距离。
g_g_dist 表示:gf自己的余弦距离。维度为15914x15914,表示每张gallery和 其他gallery的余弦距离。
最后一条代码:把三个距离矩阵送入re_ranking() 做k-reciprocal nearest neighbors的re-ranking
3.3 k-reciprocal nearest neighbors的re-ranking代码解析 :
re_ranking()函数的输入参数为3个距离矩阵。和一些默认的参数:
![]()
下面re-ranking的代码分三部分讲:
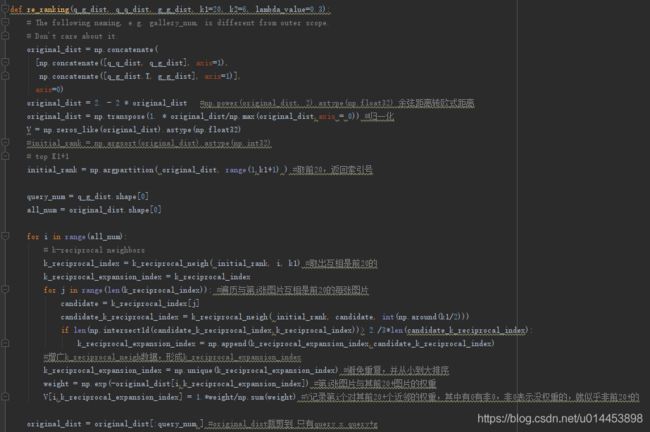
第一部分代码:
函数的第一步,是作3个距离矩阵的聚合:
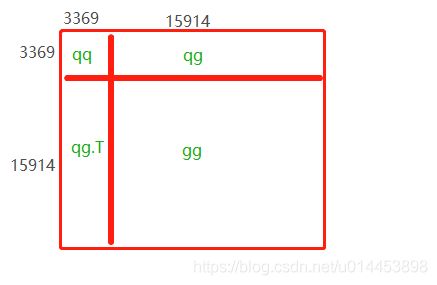
简写q_g_dist 为 qq,则得到的 original_dist 矩阵如下:
original_dist的维度是 :(3369+15914)x(3369+15914) = 19283 x 19283
19283 是 query 和 gallery 加起来的总图片数目。
所以original_dist 矩阵表示的是,全部图片各自与其他图片的余弦距离。
然后:就做余弦距离转马氏距离的操作:
![]() #这里代码少了一个平方根,应该不影响效果
#这里代码少了一个平方根,应该不影响效果
转换完马氏距离后,就做了一个归一化,把每列最大数max的找出来,然后让该列的全部成员除max,再转置:(此时的矩阵就不再对称了)
original_dist = np.transpose(1. * original_dist/np.max(original_dist,axis = 0)) #归一化解下来,就开始定义V了,V矩阵的维度和original_dist 一样,初始化为全0。
还记得V是什么吗?V是算出杰卡德(jaccard)距离的一个中间变量啊:
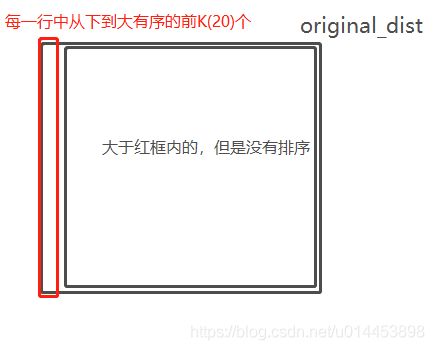
但代码这里只是先初始下 一下V,还没进行真正的操作,接下来是用original_dist 矩阵来弄出 initial rank,就是原始排列:
initial_rank = np.argpartition( original_dist, range(1,k1+1) )作用从对original_dist的每行从小到大进行排列,排前k1个(k1=20),返回的是索引号,但是original_dist维度是没有变的:
排序号之后,就成 intial_rank 了。
接着有一个大循环:
query_num = q_g_dist.shape[0]
all_num = original_dist.shape[0]
for i in range(all_num):
# k-reciprocal neighbors
k_reciprocal_index = k_reciprocal_neigh( initial_rank, i, k1) #取出互相是前20的
k_reciprocal_expansion_index = k_reciprocal_index
for j in range(len(k_reciprocal_index)): #遍历与第i张图片互相是前20的每张图片
candidate = k_reciprocal_index[j]
candidate_k_reciprocal_index = k_reciprocal_neigh( initial_rank, candidate, int(np.around(k1/2)))
if len(np.intersect1d(candidate_k_reciprocal_index,k_reciprocal_index))> 2./3*len(candidate_k_reciprocal_index):
k_reciprocal_expansion_index = np.append(k_reciprocal_expansion_index,candidate_k_reciprocal_index)
#增广k_reciprocal_neigh数据,形成k_reciprocal_expansion_index
k_reciprocal_expansion_index = np.unique(k_reciprocal_expansion_index) #避免重复,并从小到大排序
weight = np.exp(-original_dist[i,k_reciprocal_expansion_index]) #第i张图片与其前20+图片的权重
V[i,k_reciprocal_expansion_index] = 1.*weight/np.sum(weight) #V记录第i个对其前20+个近邻的权重,其中有0有非0,非0表示没权重的,就似乎非前20+的
original_dist = original_dist[:query_num,] #original_dist裁剪到 只有query x query+g很容易看出,实现的每一张图片(query+gallery)都实现以下操作:
形成一个V矩阵,
![]()
这个矩阵表示图i,对应其R星(k_reciprocal_expansion_index)每张图片的权重,当然大部分会是0,表示不相似嘛,非0的就是相似度。且V走了个归一化,权重weight除了每行weight的总和。
这一部分代码以下面一句代码结尾:
original_dist = original_dist[:query_num,] #original_dist裁剪到 只有query x query+g表示orginal_dist矩阵进行裁剪,只划到有query的地方:(3369是query集的图片数,19283是query+gallery的图片数)
第二部分代码:
第二部分就用到K2了。
这个K2跟之前的K有什么区别呢,首先K肯定是大于K2(MGN里,K2设置成6)的,我们来看看这段代码写了什么:
首先,它先创建了一个维度跟V一样的V_qe,并初始化为0。
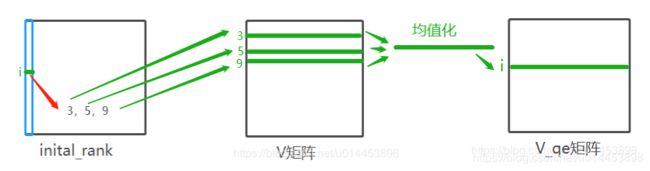
然后遍历所有图片,并进行了一个匪夷所思的操作:
![]()
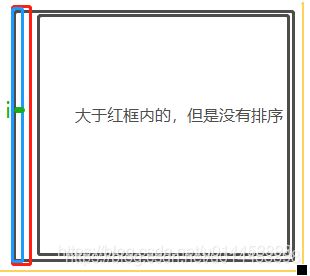
在initial_rank里,每行都取k2列,就是每张图片都取前k2个,当然我们前面已经知道initial_rank里的前k个元素(红色框)是从小打到排好序的了,因此这次取的前k2个,肯定也是从小到大排好序的:(如蓝色框)
第i行的k2就如绿色部分。当然我们前面已经知道initial_rank里的元素全是图片索引号,因此V_qe就把从initial_rank中拿出来的k2个索引号,在V中,寻找相对应的K2张图片的数据。然后再做一个均值化,把K2行数值变成一行,作为V_qe[i,:]的数据。
那这样做有什么用呢?
原理如下:
好了,得到V_qe后,V的作用就淘汰了,用V_qe直接代替V。
第三部分代码:
(ps:query_num为3369,是query集的图片数。all_num为19283,为query+gallery的图片数)
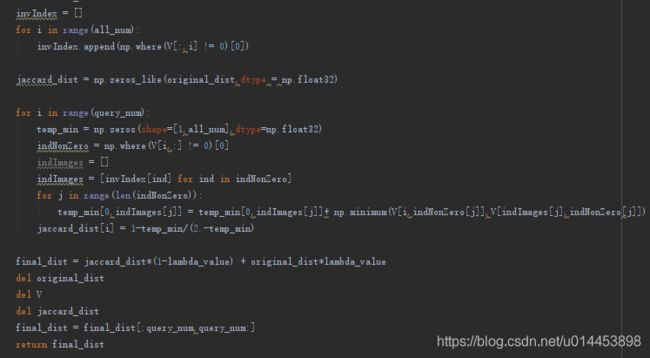
这一部分的代码功能是实现杰卡德(jaccard)距离的计算。这里比较关键的是列表 invIndex 和 indNonZero 。(注意:这里的V已经被V_qe代替了)
未免大家忘了,先前情回顾一下杰卡德距离的计算公式:
代码一开始,我们可以看到invIndex的定义:
找出V_qe矩阵每一列中不为0元素的行索引号。并把该行索引号加入到invIndex中。
然后开始定义杰卡德(jaccard)距离的维度:
可以看到jaccard_dist变量的维度和orginal_dist的维度是一样的,并初始化为0,而original_dist的维度之前已经被裁剪过变成3369x19283了:
所以jaccard_dist的维度也是3369x19283。即 (query集图片数)x(query+gallery图片数)
接下来的代码就到了一个循环:这个循环里面定义了indNonZero,indNonZero是以行为单位遍历V_qe中不为0的列,返回改行不为0元素的列索引。举个例子如下图:
由上图可以看出:
invIndex :是 以列为单位(即纵向)先遍历全部图片(query+gallery),每张图又各自与其他图作比对,返回不为0的图片号(行号)
indNonZero:invIndex完成遍历后,就开始indNonZero的遍历,和invIndex相反,indNonZero以行为单位(横向)遍历全部 图片,图上图,当遍历第一张图(i = 0行)时,返回i=0行里 不为0元素的列号,如上图V_qe中红色圈。
indImages:当i=0时,如上图V_qe中的蓝色椭圆 ,返回与图i有相似的图(0,2),然后又找与(0,2)有相似的图,0是(0,1),2是(0,1,2),正好为上图中indImages。当i继续加的时候,indImages也同理生成。
接下来就进入到一个子循环:
遍历indNonZero。
也是以 i = 0为例开始讲解,V[i,indNonZero[j]] 就是 前面图V_qe里,第i行不为0的元素的列号,如(i,0),(i,2)
可能这两行代码看起来很复杂,但其实它计算的temp_min就是下图黄色框这部分:
算出temp_min后,就可以算杰卡德(jaccard)距离了。上面的公式就是杰卡德距离公式,而代码用了一个小技巧实现:
![]()
这里可能就有小伙伴很奇怪了,怎么分母变成了 2 - temp_min呢?怎么来的呢?
为了说明,我们先举一个例子看看:
可以看出,两个向量的最大值和最小值符合这种关系:
两向量元素之和 - min的和 = max的和。反之亦然。
那怀着这个猜测,我们看看是否正确:
上述的V已经变成V_qe就不用说的了,那我们探索一下V_qe的值由谁决定,是由V决定的对不对,那我们看看V的矩阵:
前情回顾一下:
![]()
V矩阵是做了归一化的,所以V矩阵中的每一行加起来都是一,V_qe矩阵的每一行是由K2个V矩阵向量均值化而来的,因此V_qe的每一行也是加起来为1。因此两个V_qe矩阵向量加起来就为2。
所以:
杰卡德距离公式:
可以这样实现:
![]()
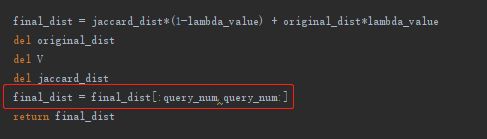
得到杰卡德距离后,就可以算最后距离(final_dist)了:
代码是:
![]()
lambda_value 作为re_ranking函数的默认参数,是人为手工设置的超参数。
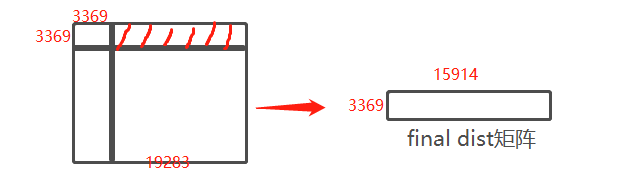
得到的final dist矩阵是:
进行裁剪 一下:
得到最后的final dist矩阵:
3369表示query集中的图片数,15914表示gallery集中的图片数。矩阵中的元素(i,j)表示query中第i张图片和gallery中第j张图片的 final dist。用作最后ranking的依据。
-----------------------------------------------------
最后奉上基于k-reciprocal Encoding的re-ranking代码:
#!/usr/bin/env python2/python3
# -*- coding: utf-8 -*-
"""
Created on Mon Jun 26 14:46:56 2017
@author: luohao
Modified by Houjing Huang, 2017-12-22.
- This version accepts distance matrix instead of raw features.
- The difference of `/` division between python 2 and 3 is handled.
- numpy.float16 is replaced by numpy.float32 for numerical precision.
Modified by Zhedong Zheng, 2018-1-12.
- replace sort with topK, which save about 30s.
"""
"""
CVPR2017 paper:Zhong Z, Zheng L, Cao D, et al. Re-ranking Person Re-identification with k-reciprocal Encoding[J]. 2017.
url:http://openaccess.thecvf.com/content_cvpr_2017/papers/Zhong_Re-Ranking_Person_Re-Identification_CVPR_2017_paper.pdf
Matlab version: https://github.com/zhunzhong07/person-re-ranking
"""
"""
API
q_g_dist: query-gallery distance matrix, numpy array, shape [num_query, num_gallery]
q_q_dist: query-query distance matrix, numpy array, shape [num_query, num_query]
g_g_dist: gallery-gallery distance matrix, numpy array, shape [num_gallery, num_gallery]
k1, k2, lambda_value: parameters, the original paper is (k1=20, k2=6, lambda_value=0.3)
Returns:
final_dist: re-ranked distance, numpy array, shape [num_query, num_gallery]
"""
import numpy as np
def k_reciprocal_neigh( initial_rank, i, k1):
forward_k_neigh_index = initial_rank[i,:k1+1] #第i个图片的前20个相似图片的索引号
backward_k_neigh_index = initial_rank[forward_k_neigh_index,:k1+1]
fi = np.where(backward_k_neigh_index==i)[0] #返回backward_k_neigh_index中等于i的图片的行索引号
return forward_k_neigh_index[fi] #返回与第i张图片 互相为k_reciprocal_neigh的图片索引号
def re_ranking(q_g_dist, q_q_dist, g_g_dist, k1=20, k2=6, lambda_value=0.3):
# The following naming, e.g. gallery_num, is different from outer scope.
# Don't care about it.
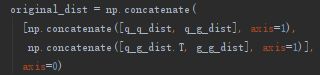
original_dist = np.concatenate(
[np.concatenate([q_q_dist, q_g_dist], axis=1),
np.concatenate([q_g_dist.T, g_g_dist], axis=1)],
axis=0)
original_dist = 2. - 2 * original_dist #np.power(original_dist, 2).astype(np.float32) 余弦距离转欧式距离
original_dist = np.transpose(1. * original_dist/np.max(original_dist,axis = 0)) #归一化
V = np.zeros_like(original_dist).astype(np.float32)
#initial_rank = np.argsort(original_dist).astype(np.int32)
# top K1+1
initial_rank = np.argpartition( original_dist, range(1,k1+1) ) #取前20,返回索引号
query_num = q_g_dist.shape[0]
all_num = original_dist.shape[0]
for i in range(all_num):
# k-reciprocal neighbors
k_reciprocal_index = k_reciprocal_neigh( initial_rank, i, k1) #取出互相是前20的
k_reciprocal_expansion_index = k_reciprocal_index
for j in range(len(k_reciprocal_index)): #遍历与第i张图片互相是前20的每张图片
candidate = k_reciprocal_index[j]
candidate_k_reciprocal_index = k_reciprocal_neigh( initial_rank, candidate, int(np.around(k1/2)))
if len(np.intersect1d(candidate_k_reciprocal_index,k_reciprocal_index))> 2./3*len(candidate_k_reciprocal_index):
k_reciprocal_expansion_index = np.append(k_reciprocal_expansion_index,candidate_k_reciprocal_index)
#增广k_reciprocal_neigh数据,形成k_reciprocal_expansion_index
k_reciprocal_expansion_index = np.unique(k_reciprocal_expansion_index) #避免重复,并从小到大排序
weight = np.exp(-original_dist[i,k_reciprocal_expansion_index]) #第i张图片与其前20+图片的权重
V[i,k_reciprocal_expansion_index] = 1.*weight/np.sum(weight) #V记录第i个对其前20+个近邻的权重,其中有0有非0,非0表示没权重的,就似乎非前20+的
original_dist = original_dist[:query_num,] #original_dist裁剪到 只有query x query+g
if k2 != 1:
V_qe = np.zeros_like(V,dtype=np.float32)
for i in range(all_num): #遍历所有图片
V_qe[i,:] = np.mean(V[initial_rank[i,:k2],:],axis=0)#第i张图片在initial_rank前k2的序号的权重平均值
#第i张图的initial_rank前k2的图片对应全部图的权重平均值
#若V_qe中(i,j)=0,则表明i的前k2个相似图都与j不相似
V = V_qe
del V_qe
del initial_rank
invIndex = []
for i in range(all_num):
invIndex.append(np.where(V[:,i] != 0)[0])
jaccard_dist = np.zeros_like(original_dist,dtype = np.float32)
for i in range(query_num):
temp_min = np.zeros(shape=[1,all_num],dtype=np.float32)
indNonZero = np.where(V[i,:] != 0)[0]
indImages = []
indImages = [invIndex[ind] for ind in indNonZero]
for j in range(len(indNonZero)):
temp_min[0,indImages[j]] = temp_min[0,indImages[j]]+ np.minimum(V[i,indNonZero[j]],V[indImages[j],indNonZero[j]])
jaccard_dist[i] = 1-temp_min/(2.-temp_min)
final_dist = jaccard_dist*(1-lambda_value) + original_dist*lambda_value
del original_dist
del V
del jaccard_dist
final_dist = final_dist[:query_num,query_num:]
return final_dist