USAD-UnSupervised Anomaly Detection on Multivariate Time Series一种基于自编码器的多元时间序列无监督异常检测
文章目录
-
- 引言
- 训练+检测架构
-
- 1. 输入
- 2. 两阶段的训练过程
- 3. 推理获得异常分数
- 4. 实验
KDD 2020年的paper,被引141次
-
论文:UnSupervised Anomaly Detection on Multivariate Time Series
-
代码:https://github.com/manigalati/usad
引言
为了解决Orange公司的IT系统自动监测异常行为所需传感器过多导致的基于专家的监督方法变慢或容易出错的问题,作者提出了一种基于自编码器AE的多元时间序列的无监督异常检测,且创新点在于受到了GANs的启发,因为作者认为基于编码-解码架构的对抗训练允许去学习“怎样去放大重建误差(在输入包含异常时)”。
论文的主要贡献可以总结如下:
- 提出了一种基于多元时间序列的无监督异常检测方法,其中对抗训练是“外壳”,里面包含的是两个自编码器的架构,以此结合了AE和GAN的双重优点,同时互相弥补了缺点,最终获得了一个性能与当前SOTA相当、同时支持快速和节能训练的异常检测的方法。具体来说:
(1)单纯的AE训练目的只是在执行最好的重构,无法检测到接近正常数据的异常;而带有对抗训练时的USAD引入了放大重建误差效应,弥补了这一缺陷。
(2)单纯的对抗训练容易产生模式崩溃和不收敛问题,而经过AE的训练之后的对抗训练可以有一个有利的初始权重,就有利于对抗训练的稳定和快速收敛。
(3)USAD:结合了AE和GAN,基于AE的架构进行两阶段的对抗训练。
训练+检测架构
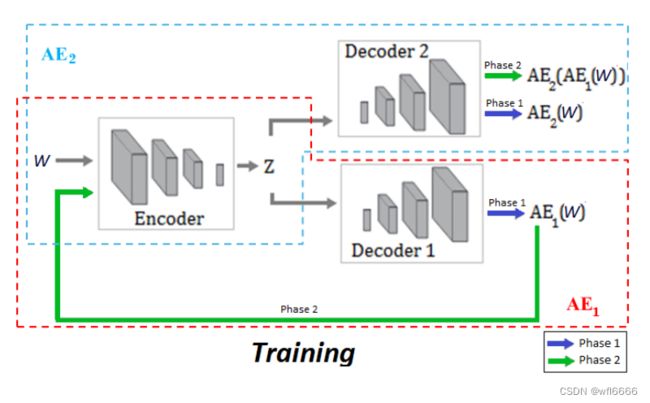
下图说明了训练阶段(左)和检测阶段(右)的信息流。
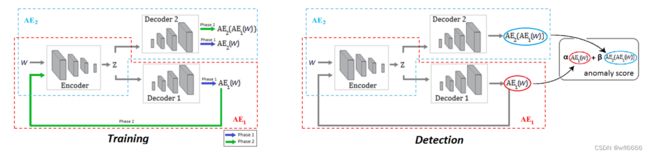
上图中均包含一个输入时间序列W,一个E,两个D;我们最想知道的应是如何进行对抗训练,以及对抗训练的目的是什么,为什么实施对抗训练之后可以检测到接近正常的异常了?
1. 输入
下面我们先来了解一下用于训练和检测的输入❀W是什么,以便把问题公式化:
- W t _t t:我们首先用W t _t t来表示一个在 t 时刻长度为 K 的时间窗口,即
W t _t t={x t − K + 1 _{t-K+1} t−K+1,…,x t − 1 _{t-1} t−1,x t _t t},其中,x∈R m ^m m,K是时间窗口,而且是滑动时间窗口,考虑的是当前时刻与之前时刻的数据的时间相关性
如果我们想用视频去构造一个多变量时间序列,那么x∈R W ∗ H ∗ 3 ^{W*H*3} W∗H∗3即可,表示K帧视频数据
- ❀W:是一个序列,用于作为训练和检测的输入数据
❀W={W 1 _1 1,…,W 2 _2 2,W T _T T} , 其中 T 是代码中的batch_size:7919
2. 两阶段的训练过程
phase 1 : 训练两个基础的AE,完成对输入❀W 的良好重构。不再赘述,采用均方根loss:
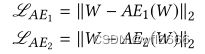
phase 2 : 这里是论文比较大的创新,借鉴了GAN的训练方式。对两个网络进行对抗训练。
在这里AE2充当鉴别器D,AE2的目的是最大化AE2(AE1(W))与W的不同,从而能够区分真实的输入W和AE 1 _1 1(W)(严格意义上来说,AE2并不算真正的D,因为AE2的另一个作用是当输入是W时,仍然执行最好的重构)。AE1则充当生成器,目的是最小化AE2(AE1(W))与W的不同,从而迷惑AE2,让AE2区分不出真实的输入数据和AE1重构出来的数据。
在这个阶段的loss表示为:
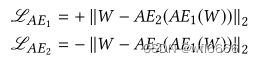
现在将两阶段合起来,Loss合并如下,n为epoch数:
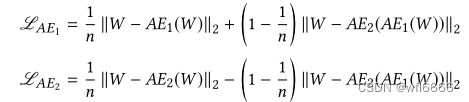
至此,训练完成之后,AE2就有了区分真实输入数据还是经过AE1重构后的数据的能力。 强调这一点是因为在推理阶段定义异常分数的时候,要用到这里。
3. 推理获得异常分数
下式是在推理阶段定义的异常得分的公式:
![]()
作者提到 α + β = 1,是一个在假阳性(false positives)和真阳性(true positives)之间的权衡参数。有两种情况,说一下我的理解:

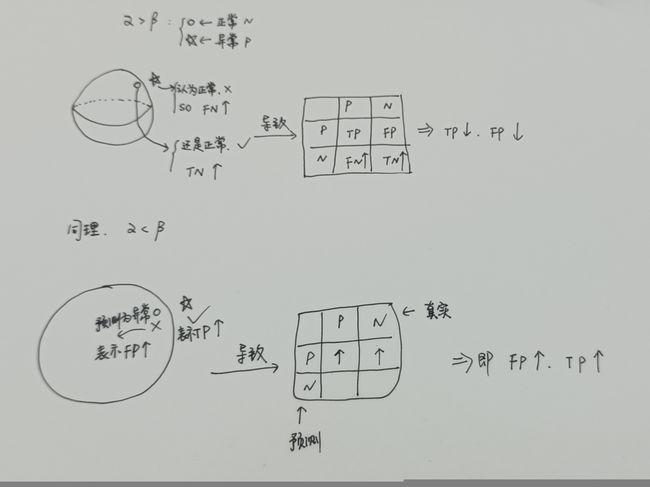
α > β :结论—> TP ↓ 并且 FP ↓
看异常得分的公式,α大的话,那么异常得分更加取决于AE1(W)与W之间的重建误差,此时与只训练AE没多大区别,于是那些接近正常的异常会因为重构的比较好被认为是正常,也就是FN会增加,相应的TP↓ ;而正常的就很容易被认为是正常,TN ↑ ,那么FP ↓ ,这就是低灵敏度检测。
α < β :结论—> TP ↑ 并且 FP ↑
还是看异常得分的公式,β大的话,那么异常得分更加取决于AE1(W)作为AE2的输入时得到的输出AE2(AE1(W))与W之间的重建误差,此时就体现出对抗训练的作用了,于是那些接近正常的异常会因为重构的比较差(因为AE2能辨别输入是W还是AE1(W),辨别出是AE1(W)时会进行最大化误差),被正确的认为是异常,也就是TP↑,相应的FN↓ ;但是同时在正常边界的正常就很容易因为误差被拉大而被认为是异常,FP ↑ ,那么TN ↓,这就是高灵敏度检测。
论文里说,这样一个参数化的方案就很好的实现了一个工业需求,即允许使用一个单一的模型,在推理期间可以获得不同灵敏度的分数。
这篇跟之前博客写过的一片GCL生成式协作学习很相似,还需要仔细对比一下两者之间的区别于联系,因为二者目的也是一样的。
对于本篇论文我还不太明白的一点是,既然AE2的作用仅仅是轻微放大与输入之间重建误差,那为什么还要训练两个阶段,首先去训练它的良好重构能力呢?两个目的似乎是矛盾的,但这就是AE2的两个作用。对此,我目前认为的解释还是这个推理算法和异常得分公式来看:

![]()
对于得分公式的α部分没有什么疑问,β部分,表明了AE2的输入是AE1(W),即W经过AE1重构的输出,此时,AE2的作用体现,虽然我们明确知道输入是AE1(W),但是AE2其实真正区分的应该是正常和接近正常的异常,而不是论文一直提到的AE2的作用是区分输入还是经过AE1重构后的输入(误导人啊!)。因为如果我们真的认为AE2是来区分输入的,那么AE2的作用就真的只有拉大误差的作用。但是如果我们认为AE2是区分正常数据还是异常数据的,那么AE2的两个作用(也是论文提到的)才真正体现:
-
输入W是正常数据时,AE1(W)也在正常范围内,此时AE2认为输入的AE1(W)是正常数据,则进行良好的重构,也就会减少把在正常边界区域的正常经过拉大误差判断为异常的情况。
-
输入W是接近正常的异常数据时,AE1(W)轻微异常,此时AE2才会进行误差拉大的操作,所以对抗训练其实就是为了拿AE1去训练AE2让AE2获得一个良好的区分正常和异常数据的能力。
以上是我的个人理解,有理解不当之处,敬请批评指正!
-------更正:AE2的两个作用应是在不同的训练阶段体现的,不是上面的理解。
4. 实验
实验部分下载了原论文的源码通了一遍,同时查看了SWaT数据集的内容,是一个工业水处理厂的一些数据,就是真正的多变量时间序列。K设置为12,T是7919。