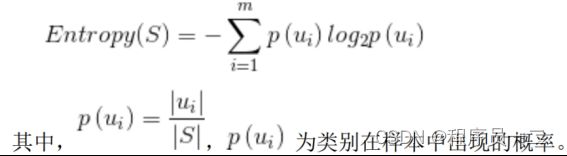基于决策树算法对良/恶性乳腺癌肿瘤预测

本人数据结构课程设计如题所示，现给出该课设的具体设计思路及代码演示，供大家学习，交流，共同学习（部分代码借鉴GitHub大佬）

内容简介：

       决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。信息熵（Entropy ）= 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。本课设采用ID3算法。

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。

决策树是一种十分常用的分类方法。它是一种监督学习，所谓监督学习就是给定一堆样本，每个样本都有一组属性和一个类别，这些类别是事先确定的，那么通过学习得到一个分类器，这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。

决策树是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法。它是一个从上到下、分而治之的归纳过程，是决策树的一个经典的构造算法。应用于很多预测的领域，如通过对信用卡客户数据构建分类模型，可预测下一个客户他是否属于优质客户。再如本课设所研究的根据乳腺癌细胞的各种特征，来预测该乳腺癌肿瘤为良性还是恶性。

（一）需求和规格说明

本次数据结构课程设计采用的数据集为 UCI 网站上的 breast-cancer-wisconsin 数据集。数据共有 10 个属性，1 个分类，训练和测试时采用 4-10 号属性，预测 11 号分类。

部分数据集如下图所示：

根据题目要求，对于给定的训练数据集，我们构建出了决策树模型。然后评价预测模型的好坏，我们对位置类别属性数据样例进行分类，并与真实结果比较后得到预测模型的学习效果和泛化性能。

在交叉验证时，输入 590 个数据作为训练数据，98 个数据作为测试数据。

数据集及测试集下载链接：https://pan.baidu.com/s/1BcOY6YzlodazVYNyFXPDKg?pwd=y6af 
提取码：y6af

（二）设计

2.1 设计初衷

由于本人现为人工智能与大数据校企共建实验室的成员，平时对于机器学习算法兴趣颇丰，对于结构化数据的机器学习处理有一定了解，故选了决策树算法这道课程设计题。其次，选题的另一大原因是自己也在致力于明年国家级大创的申请，选题是基于基因表达数据对多种癌症特征基因选择和识别的系统设计与实现，其中决策树算法只是那个项目集成学习中的一个基学习器。而本课设我也是基于乳腺癌细胞的各种特征的数据，使用最基本的ID3算法，实现决策树预测模型的构建，并对测试集进行模型的评估。

机器学习一般都是用Python语言实现的，由于本课设要求使用C++语言，基于ID3算法构建出决策树模型，并进行评估，所以写起来也是一个较大的工程量，没有那么轻松。想要实现这个程序需要掌握很多预备知识：对于ID3算法的了解，会用编程语言来计算信息熵、信息增益等数据，运用递归和决策树的思想构建出决策树这一数据结构。

接下来我将详细介绍，我最终课程设计的设计背景与设计细节。

2.2 设计背景

H.Simon 曾于1983 年给出了一个关于学习的哲学式说明：如果一个系统能够 通过执行某种过程而改进其性能，这就是学习。机器学习是一门多领域交叉学科，专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能，当前机器学习正被应用于各个领域（交通、医疗等等），它的重要性不言而喻。

李航的《统计学习方法》为我们介绍了机器学习中监督式学习的三种决策树算法：ID3,C4.5,CART，使之前没有接触过相关内容的我对机器学习有了一个最基本的 了解，并在本次数据结构课程设计中尝试对 ID3算法进行代码实现。

在谈设计细节前，我们需要对ID3算法进行简单介绍。

ID3算法是决策树算法中最简单的算法，其主要是通过信息增益来进行特征的选择，根据公式选择最优子项（纯度最高）继续向下分裂来建树。ID3 算法的核心是采用贪婪策略，通过信息增益来计算下一个分类目标，而信息增益的核心为信息熵，熵起源于物理学，是上世纪五十年代由香农引进用来表示不确定量。信息熵是影响信息益变化的关键，信息熵越低就表示整个系统会更加的有序。

信息熵(Entropy)

信息增益(Information gain)

了解完决策树算法的核心以及如何计算信息熵和信息增益后，我们就可以开始基于ID3算法的决策树设计。

2.3 设计细节

2.3.1信息熵的计算

根据属性的取值，我们要先计算该属性的信息熵，然后才能进行后续的计算。那么输入值为不同组数据中某种属性或分类的取值集合，例如classes：（2，2，4，4，2，2，4，4，2......）。

首先我们需要去掉重复元素，提高模型的泛化能力。最后遍历例如classes的每种取值，根据上面给出的信息熵计算公式，计算概率*log2（概率），取负后加入entropy（信息熵）。遍历结束即可返回entropy，即该属性的信息熵。

2.3.2信息增益的计算

其次我们需要计算数据集中所有属性的信息增益，输入为训练集（二维vector数组）。

先要用动态数组存储各个属性的信息增益，规模数为truths的size-1是因为训练集各个数据的最后一列为classes，无需计算。然后针对每个属性存储其取值，得到该属性在各个数据中的取值集合。接着存储classes的取值，将classes取值放入labels，遍历每一种属性，其中最后一列是类别标签，没必要计算信息增益。得到第i种属性取*itr的概率以及该属性取值对应classes的信息熵，加到H(D|A)中。

最后得到信息增益：

gain[i] =compute_entropy(labels) - gain[i];//g(D,A)=H(D)-H(D|A)

2.3.3决策树的构建

首先我们需要对决策树的结构体进行封装，我采用了书上一种简单的封装方式。

struct Tree {

unsigned root;//节点属性值

vector branches;//节点可能取值

vector children; //孩子节点

};

这样通过递归，分而治之的思想以及信息增益的数据支持我们就可以顺利构建出决策树。

递归构建决策树：

第一步：判断所有实例是否都属于同一类，如果是，则无需划分，决策树是单节点(递归出口)；

第二步：判断是否还有剩余的属性没有考虑，如果所有属性都已经考虑过了，则无法划分，那么此时属性数量为0，将训练集中最多的类别标记作为该节点的类别标记(递归出口)；

第三步:在上面两步的条件都判断失败后，计算信息增益，选择信息增益最大的属性作为根节点，并找出该节点的所有取值；

第四步：根据节点的取值，将examples分成若干子集(子树都是在分支的条件下建立)；

第五步：对每一个子集递归调用递归构建决策树函数。

2.3.4决策树的打印

由于决策树的数据结构性质，我们采用递归的思想将它的结点打印出来。对于根节点和内部节点打印它的标签和取值；对于叶子结点，我们就可以直接打印它的属性值（良性：2；恶性：4）。

2.3.5决策树的性能评估

我们根据已经建立好的决策树模型预测训练集和测试集中的每个样例，并得到训练集和测试集的成功率，从而实现的决策树的性能评估。

（三）运行实例

由于决策树的高度较大，限于篇幅，仅截部分运行实例如图所示。  

完整模型请运行程序在命令行上阅览。

训练集成功率为1

测试集成功率为0.938776

（四）进一步改进

（1）界面单一。由于初次接触决策树算法，编写出来的决策树架构只是简单地通过分隔符的控制打印输出，以后可以使用QT界面更直观地画出决策树模型。但我觉得重点是预测，模型的展示是一种对程序可视化的表现，也很重要。

（2）可操作性空间不够。因为决策树的构建以及对于数据的处理是一个大工程，它包括数据清洗等等很多前期的工作，本课设只实现了一个预测模型的核心构建，所以没有太完善，明年的国家级大创对预测系统的构建肯定会相对完善。

（3）算法性能不高。因为使用的是ID3算法，是决策树模型构建中最简单的算法。它有很大的局限性，缺点如下：

1.ID3只考虑分类型的特征，没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。这大大限制了ID3的用途。

2.ID3算法对于缺失值没有进行考虑。

3.没有考虑过拟合的问题。

4.ID3算法在选择根节点和各内部节点中的分支属性时，采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息。

5.划分过程会由于子集规模过小而造成统计特征不充分而停止。

我会尝试使用别的算法，例如：C4.5、CART算法从而得到更好的预测模型。

（五）心得体会

通过本次课程设计，个人感觉是受益匪浅的，首先先感谢这次课程设计所给我带来的收获。

对于这次的课程设计，我更加深入地学习了机器学习的决策树相关知识，递归算法的应用，树这种存储结构的构建。可以说整个程序大部分的代码都是建立在新知识的基础上，以及这一学期所学的关于递归、树的知识。我认为这对我的编程能力是有极大提升的，是对有限学时的巨大补充，也提高了我的调参能力和修改bug能力，这也有助于我暑假对机器学习的研究以及后面的大创工作。

网课资源和各大平台资源（GitHub、CSDN）对于大学生来说是非常重要的，它能够让你学到课堂因学时有限所学不到的内容，从而让你获得编码能力上的提升，我想这也是我们合肥工业大学课程设计的目的所在。

调参能力与修改bug能力这是我们计算机科学与技术专业的学生所要面对的问题，而在课程设计中这些能力就能得到较大的提升，实践才能出真知！在规定的时间，规定的项目方向尽可能地完成它，我觉得这次的课程设计能反映我目前个人较好的编码能力。如果代码和功能存在一些致命性问题，还望老师多多批评指正，我会虚心接受，努力修改。未来可期，希望有更多的课程设计机会来锻炼我，让我的编码能力得到进一步的提升！

（六）代码实现

下面给出具体的代码实现（含大量注释），以便读者更好的理解本人的设计思想。

/*
该决策树应用的算法为ID3——决策树中选择最优划分属性最基本的一个方法，当然还有CART、C4.5算法
该决策树应用的数据集为判断乳腺癌为良性（classes:2）或为恶性（classes:4）
该数据集的属性共有10个，训练和测试时选择了属性4-10，每个属性的值为1-10(减少属性数量，提高泛化能力)——举例大创工作（小样本，高维度）
运行代码输出决策树，输出将训练集放入决策树的成功率，交叉验证并输出将测试集放入决策树的成功率
*/

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

vector> trains;//训练集内容，包含了590个训练样例
vector> tests;//测试集内容，包含了98个测试样例

//属性名称，作用于打印决策树
string attribute_names[] = { "Uniformity of Cell Shape", "Marginal Adhesion", "Single Epithelial Cell Size","Bare Nuclei","Bland Chromatin","Normal Nucleoli","Mitoses" };

//数据集中各个属性的所有可能取值，与attribute_names[]中的元素按顺序对应，用于打印
unsigned attribute_values[] = { 1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10,2,4 };

//将所有属性和分类的可能取值与0-71一一对应，读取数据集时将数据转化为对应的attribute_number，方便编程(从0开始在print里方便调用数组下标)。（本数组仅作后续讲解，不使用）
unsigned attribute_number[] = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71 };


//将数据读入训练集和测试集，并转换为对应的数字，存入动态数组trains和tests

void read_file()
{
	vector s;//暂存数据集中的每一行

	//10种属性和1种类别，前三种属性忽略
	unsigned codeNumber;// 分支节点纯度达到最大，不具有泛化能力，无法对新数据进行预测（过拟合）
	unsigned thickness;
	unsigned size;
	unsigned shape;
	unsigned adhesion;
	unsigned cellSize;
	unsigned nuclei;
	unsigned chromatin;
	unsigned nucleoli;
	unsigned mitoses;
	unsigned classes;
	
	

	//训练集
	fstream is;
	is.open("breast-cancer.data");

	if (is)
	{
		while (!is.eof())
		{
			is >> codeNumber >> thickness >> cellSize >> shape >> adhesion >> size >> nuclei >> chromatin >> nucleoli >> mitoses >> classes;
			//转换为对应数字
			//转换举例：
			//转化前：1000025 5 1 1 1  2  1  3  1  1  2
			//转化后：            0 10 21 30 42 50 60 70 
			s.push_back(shape - 1);
			s.push_back(adhesion + 9);
			s.push_back(size + 19);
			s.push_back(nuclei + 29);
			s.push_back(chromatin + 39);
			s.push_back(nucleoli + 49);
			s.push_back(mitoses + 59);
			if (classes == 2) //最后一列为分类标签
				s.push_back(70);
			else
				s.push_back(71);

			trains.push_back(s);
			s.clear();
		}
	}
	is.close();

	//测试集
	fstream tis;
	tis.open("test.data");
	if (tis)
	{
		while (!tis.eof())
		{
			tis >> codeNumber >> thickness >> cellSize >> shape >> adhesion >> size >> nuclei >> chromatin >> nucleoli >> mitoses >> classes;

			s.push_back(shape - 1);
			s.push_back(adhesion + 9);
			s.push_back(size + 19);
			s.push_back(nuclei + 29);
			s.push_back(chromatin + 39);
			s.push_back(nucleoli + 49);
			s.push_back(mitoses + 59);
			if (classes == 2)
				s.push_back(70);
			else
				s.push_back(71);
			tests.push_back(s);
			s.clear();
		}
	}
	tis.close();
}


//计算一个数值得以2为底的对数

double log2(double n)
{
	return log10(n) / log10(2.0);
}

//将vector中重复元素合并，只保留一个

template 
vector unique(vector vals)
{
	vector unique_vals;
	typename vector::iterator itr;
	typename vector::iterator subitr;

	int flag = 0;
	while (!vals.empty())
	{
		unique_vals.push_back(vals[0]);
		itr = vals.begin();
		subitr = unique_vals.begin() + flag;
		while (itr != vals.end())
		{
			if (*subitr == *itr)
				itr = vals.erase(itr);
			else
				itr++;
		}
		flag++;
	}
	return unique_vals;
}

//根据属性的取值，计算该属性的信息熵

double compute_entropy(vector v) //输入为不同组数据中某种属性或分类的取值集合，例如classes：（2，2，4，4，2，2，4，4，2......）
{
	vector unique_v;
	unique_v = unique(v);//去掉重复元素，在本数据集中即（2，4）

	vector::iterator itr;
	itr = unique_v.begin();

	double entropy = 0.0;
	auto total = v.size();
	while (itr != unique_v.end())//遍历classes的每种取值，计算 概率*log2（概率），取负后加入entropy
	{
		double cnt = count(v.begin(), v.end(), *itr);//计算每种classes取值在集合中的个数
		entropy -= cnt / total * log2(cnt / total);
		itr++;
	}
	return entropy;
}

//计算数据集中所有属性的信息增益
vector compute_gain(vector > truths)//输入为训练集
{
	vector gain(truths[0].size() - 1, 0);//存储各个属性的信息增益，规模数为truths的size-1是因为训练集各个数据的最后一列为classes，无需计算
	vector attribute_vals;//用来针对每个属性存储其取值，得到该属性在各个数据中的取值集合
	vector labels;//用来存储classes的取值
	for (unsigned j = 0; j < truths.size(); j++)//将classes取值放入labels
	{
		labels.push_back(truths[j].back());
	}

	for (unsigned i = 0; i < truths[0].size() - 1; i++)//遍历每一种属性，最后一列是类别标签，没必要计算信息增益
	{
		for (unsigned j = 0; j < truths.size(); j++)//将每个数据j中的第i种属性的取值放入attribute_vals
			attribute_vals.push_back(truths[j][i]);

		vector unique_vals = unique(attribute_vals);//去重，得到第i种属性的所有可能取值
		vector::iterator itr = unique_vals.begin();
		vector subset;//subset存储对应于数据的第i种属性为某个取值时的classes集合
		while (itr != unique_vals.end())//遍历第i种属性的所有可能取值
		{
			for (unsigned k = 0; k < truths.size(); k++)
			{
				if (*itr == attribute_vals[k])
				{
					subset.push_back(truths[k].back());//将数据truth[k]的第i种属性取*itr时的classes放入subset
				}
			}
			double A = (double)subset.size();
			gain[i] += A / truths.size() * compute_entropy(subset);//得到第i种属性取*itr的概率以及该属性取值对应classes的信息熵，加到H(D|A)中
			itr++;//计算第i种属性的下一个取值
			subset.clear();
		}
		gain[i] = compute_entropy(labels) - gain[i];//g(D,A)=H(D)-H(D|A)
		attribute_vals.clear();
	}
	return gain;
}


//找出数据集中最多的类别属性

template 
T find_most_common_label(vector > data)
{
	vector labels;
	for (unsigned i = 0; i < data.size(); i++)
	{
		labels.push_back(data[i].back());
	}
	typename vector::iterator itr = labels.begin();
	T most_common_label;
	unsigned most_counter = 0;
	while (itr != labels.end())
	{
		unsigned current_counter = count(labels.begin(), labels.end(), *itr);
		if (current_counter > most_counter)
		{
			most_common_label = *itr;// 返回最多的类别属性
			most_counter = current_counter;
		}
		itr++;
	}
	return most_common_label;
}


//根据属性，找出该属性可能的取值

template 
vector find_attribute_values(T attribute, vector > data)
{
	vector values;
	for (unsigned i = 0; i < data.size(); i++)
	{
		values.push_back(data[i][attribute]);
	}
	return unique(values);
}

/*
在构建决策树的过程中，如果某一属性已经考察过了
那么就从数据集中去掉这一属性，此处不是真正意义
上的去掉，而是将考虑过的属性全部标记为100
*/

template 
vector > drop_one_attribute(T attribute, vector > data)
{
	vector > new_data(data.size(), vector(data[0].size() - 1, 0));
	for (unsigned i = 0; i < data.size(); i++)
	{
		data[i][attribute] = 100;
	}
	return data;
}

//决策树的结构体封装
struct Tree {
	unsigned root;//节点属性值
	vector branches;//节点可能取值
	vector children; //孩子节点
};

//递归构建决策树
void build_decision_tree(vector > examples, Tree& tree)// （子集）集合，（子树）根结点
{
	//第一步：判断所有实例是否都属于同一类，如果是，则无需划分，决策树是单节点(递归出口)
	vector labels(examples.size(), 0);
	for (unsigned i = 0; i < examples.size(); i++)
	{
		labels[i] = examples[i].back();// 返回数组最后一个单元：classes
	}
	if (unique(labels).size() == 1)
	{
		tree.root = labels[0];
		return;
	}

	//第二步：判断是否还有剩余的属性没有考虑，如果所有属性都已经考虑过了，则无法划分
	//那么此时属性数量为0，将训练集中最多的类别标记作为该节点的类别标记(递归出口)
	if (count(examples[0].begin(), examples[0].end(), 100) == examples[0].size() - 1)//只剩下一列类别未被标记为100
	{
		tree.root = find_most_common_label(examples);
		return;
	}
	//第三步:在上面两步的条件都判断失败后，计算信息增益，选择信息增益最大的属性作为根节点，并找出该节点的所有取值

	vector standard = compute_gain(examples);//计算信息增益

	tree.root = 0;
	for (unsigned i = 0; i < standard.size(); i++)//选择信息增益最大的属性作为根节点
	{
		if (standard[i] >= standard[tree.root] && examples[0][i] != 100)
			tree.root = i;
	}

	tree.branches = find_attribute_values(tree.root, examples);//找出该节点的所有取值

	//第四步：根据节点的取值，将examples分成若干子集(子树都是在分支的条件下建立)
	vector > new_examples = drop_one_attribute(tree.root, examples);//已考察属性要先作处理再开始分
	vector > subset;
	for (unsigned i = 0; i < tree.branches.size(); i++)//分支
	{
		for (unsigned j = 0; j < examples.size(); j++)//行数
		{
			for (unsigned k = 0; k < examples[0].size(); k++)//列数
			{
				if (tree.branches[i] == examples[j][k])
					subset.push_back(new_examples[j]);
			}
		}
		//第五步：对每一个子集递归调用build_decision_tree()函数
		Tree new_tree;
		build_decision_tree(subset, new_tree);
		tree.children.push_back(new_tree);
		subset.clear();
	}
}

//递归打印决策树

void print_decision_tree(Tree tree, unsigned depth)
{
	for (unsigned d = 0; d < depth; d++) cout << "\t";
	if (!tree.branches.empty()) //根节点和内部节点
	{
		cout << attribute_names[tree.root] << endl;

		for (unsigned i = 0; i < tree.branches.size(); i++)
		{
			for (unsigned d = 0; d < depth + 1; d++) cout << "\t";
			cout << attribute_values[tree.branches[i]] << endl;// 将转化后的数据转化为转化前的取值（1-10）
			print_decision_tree(tree.children[i], depth + 2);
		}
	}
	else //是叶子节点
	{
		cout << attribute_values[tree.root] << endl;
	}

}

//根据已经建立好的决策树模型预测数据集中的每个样例

unsigned classify_tree(Tree tree, vector test)
{
	if (tree.branches.empty())//是叶子节点
	{
		return tree.root;
	}
	else
	{
		for (unsigned i = 0; i < tree.branches.size(); i++)
		{
			if (test[tree.root] == tree.branches[i])
			{
				return classify_tree(tree.children[i], test);
			}
		}
	}
}

//检测决策树学习效果和泛化性能

void test_tree(Tree tree)
{
	unsigned num_right_test = 0;
	unsigned num_right_train = 0;

	unsigned result;

	double right_ratio_test;
	double right_ratio_train;

	//训练集，得出学习效果
	for (unsigned i = 0; i < trains.size(); i++)
	{
		result = classify_tree(tree, trains[i]);
		if (result == trains[i].back())
			num_right_train++;
	}
	right_ratio_train = double(num_right_train) / trains.size();
	cout << endl;
	cout << "训练集成功率为" << right_ratio_train;

	//测试集，得出泛化性能
	for (unsigned i = 0; i < tests.size(); i++)
	{
		result = classify_tree(tree, tests[i]);
		if (result == tests[i].back())
			num_right_test++;
	}
	right_ratio_test = double(num_right_test) / tests.size();
	cout << endl;
	cout << "测试集成功率为" << right_ratio_test;
}



int main()
{

	read_file();//读取训练集的数据入动态数组trains,读取测试集的数据入动态数组tests

	Tree tree;//创建一棵决策树
	build_decision_tree(trains, tree);

	print_decision_tree(tree, 0);//打印决策树

	test_tree(tree);//将训练集数据和测试集数据分别放入决策树进行测试，输出各自的预测成功率，得到学习效果和推广性能

	return 0;
}

部分代码借鉴GitHub大佬的开源代码，如有不足之处，欢迎指出，共同学习！