计算智能-遗传算法二

一、算法介绍

关于本算法的原理介绍在之前的博客中已经提到过了，这边就不细说了。详情请点击此处 计算智能-遗传算法.
上一博客中讲述的遗传算法是求tsp问题的最短路径，但是在上一种解法，我们是对函数进行优化，属于局部的优化，该算法找到的哈密顿回路很可能是局部的最优解，本次遗传算法要进行的是一种全局优化，尽可能的找到符合条件的哈密顿回路。

二、算法主要代码

1、cross.m

function [A,B]=cross(A,B)
L=length(A);
if L<10
    W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
    W=ceil(L/10)+8;
else
    W=floor(L/10)+8;
end
%%W为需要交叉的位数
p=unidrnd(L-W+1);%随机产生一个交叉位置
%fprintf('p=%d ',p);%交叉位置
for i=1:W
    x=find(A==B(1,p+i-1));
    y=find(B==A(1,p+i-1));
    [A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
    [A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end

该函数进行交叉位置的判断，交换城市时，观察城市序列中是否会包含重复城市；若重复了，则增加一个交换操作。

2、exchange.m

%对调函数 exchange.m

function [x,y]=exchange(x,y)
temp=x;
x=y;
y=temp;
 
end

该函数实现了两个城市的坐标互换

3、fit.m

function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
    fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end

该函数为适应度函数，每次迭代都要计算每个染色体在本种群内部的优先级别，类似归一化参数。越大越好！

4、Mutation.m

function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;

end

该函数为变异函数

5、 mylength.m

function len=myLength(D,p)%p是一个排列
[N,NN]=size(D);
len=D(p(1,N),p(1,1));
for i=1:(N-1)
    len=len+D(p(1,i),p(1,i+1));
end
end

该函数为计算染色体的路程代价

6、plot_route.m

function plot_route(a,R)
scatter(a(:,1),a(:,2),'rx');
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
    x0=a(R(i-1),1);
    y0=a(R(i-1),2);
    x1=a(R(i),1);
    y1=a(R(i),2);
    xx=[x0,x1];
    yy=[y0,y1];
    plot(xx,yy);
    hold on;
end
end

该函数为连点画图函数

三、运行结果

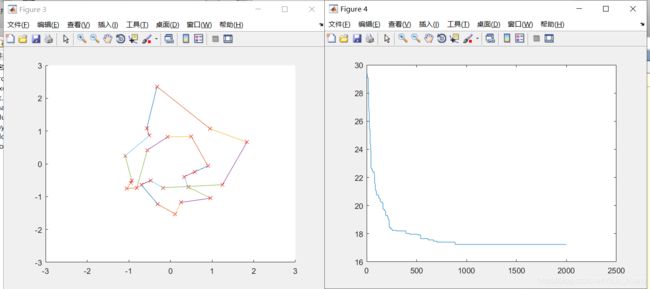
1、交叉概率为0.8，变异概率为0.05，城市位置不变，种群个数改变时：

M=100时 minlen=1.731907e+01

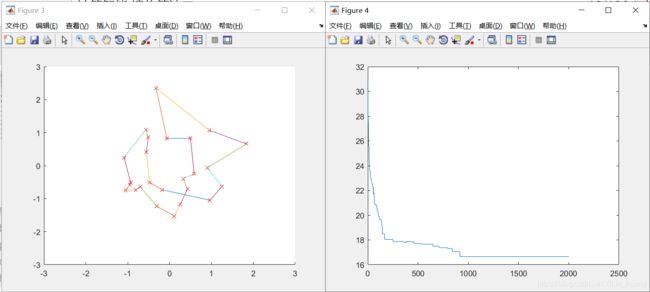
M=150时，minlen=1.403934e+01

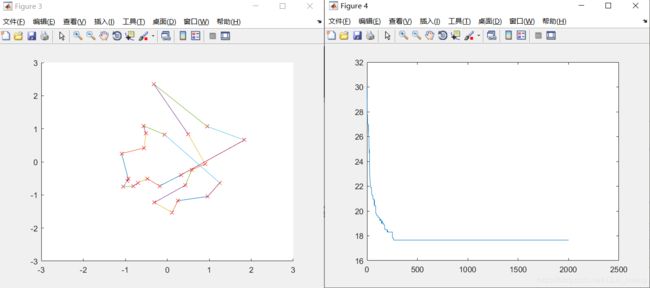
M=200时，minlen=1.402738e+01

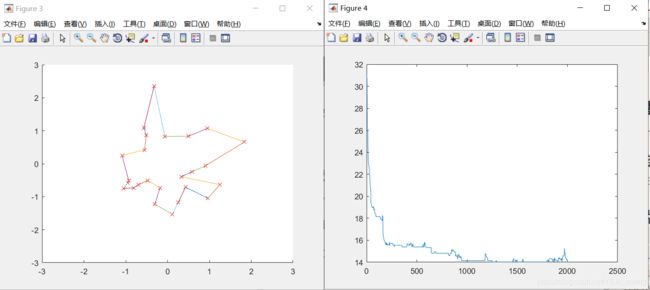
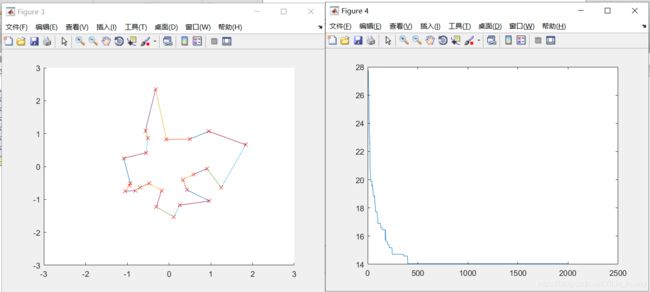
2、交叉概率为0.8，变异概率为0.05，城市位置不变，种群个数为100，迭代次数的改变：

ITER=1000，minlen=1.697324e+01

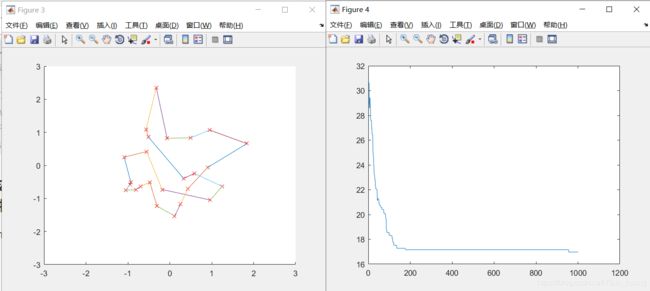
ITER=2000，minlen=1.677544e+01

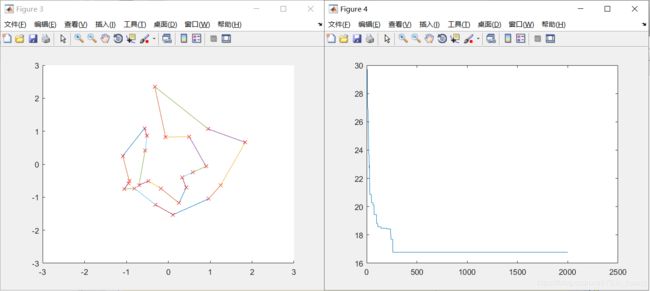
ITER=3000，minlen=1.597454e+01

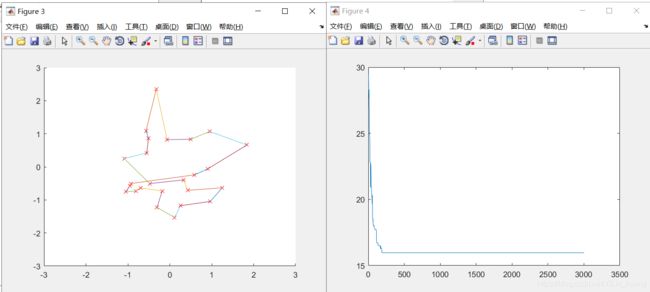
3、变异概率为0.05，城市位置不变，种群个数为100，迭代次数2000，交叉概率的改变：

Pc=0.1;

Pc=0.5;

Pc=0.8;

4、交叉概率为0.8，城市位置不变，种群个数为100，迭代次数2000，变异概率的改变：

Pmutation=0.01;

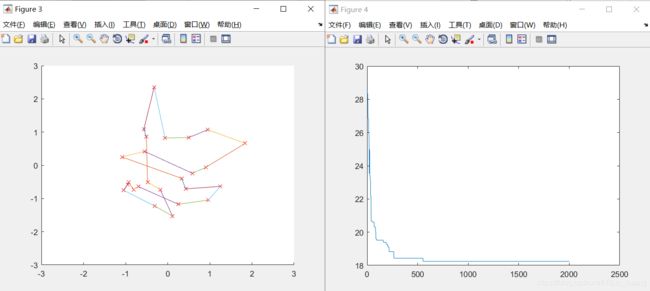
Pmutation=0.05;

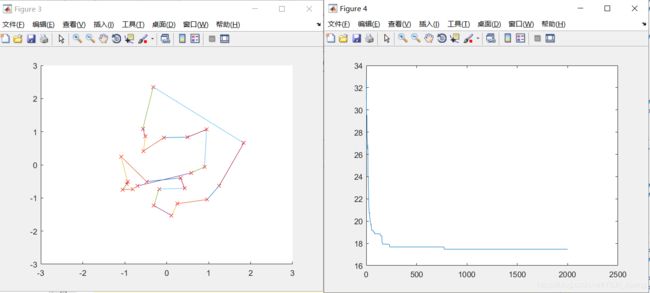
Pmutation=0.1;

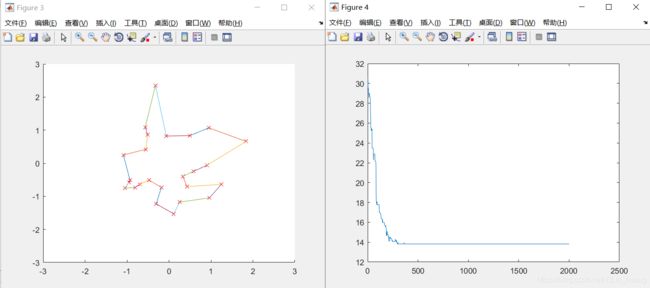
四、结果分析

1、对于种群数量的改变：其他参数不变的前提下，随着种群个数的增多，路径总长达到收敛时的迭代次数与最短距离的变化趋势都是不断减少的；在种群数量不断地增多的情况下有利于函数的收敛，找到最短路径；但种群数目不能过大，否则，将起到相反作用。
2、对于迭代次数的改变：在其他参数不变的情况，迭代次数的增多没有对结果产生太大的影响。但是如果在城市数量超过50的情况下，迭代次数必须要足够多才能够找到最短路径，太少的情况下可能会找到一个局部最优解
3、对于交叉概率的改变：在其他条件不改变的情况下，随着交叉概率的上升，函数的收敛速度也就越快，迭代次数越少，经过测试，交叉概率越接近1，效果越明显
4、对于变异概率的改变：在其他参数不改变的情况下，随着变异概率的增多，路径总长达到收敛时的迭代次数变动频繁，最短距离也越来越大，由此可知，Pm的值不宜过大，变异会破坏已找到的较优解。Pm值过大可能会导致反效果。这里的测试值为【0.01,0.1】。