【智能控制实验】基于MATLAB的遗传算法函数优化问题求解
基于MATLAB的遗传算法函数优化问题求解实验报告
一、实验要求:
掌握matlab遗传算法工具箱的函数命令实现函数优化问题的方法和图形用 户界面下求解优化问题的方法。
- 利用matlab工具箱函数命令实现函数的优化:
已知:
(1)f(x)=x+10sin(5x)+7cos(4x)
优化问题:
Max f(x), s. t. 15£ x£25
绘出函数图像,并给出matlab工具箱函数命令下应用遗传算法求解优化问题的结果和结果分析。
优化问题:
Max f(x,y), s. t. -3£x£3,-3£y£3
绘出函数图像,并给出matlab工具箱函数命令下应用遗传算法求解优化问题的结果和结果分析。
2、图形用户界面下应用遗传算法求解优化问题:
已知:
(1)f(x)=x+10sin(5x)+7cos(4x)
优化问题:
Max f(x), s. t. 15£ x£25
给出图形用户界面下应用遗传算法求解优化问题的结果和结果分析。
优化问题:
Max f(x,y), s. t. -3£x£3,-3£y£3
给出图形用户界面下应用遗传算法求解优化问题的结果和结果分析。
二、实验内容
2.1 利用matlab工具箱函数命令实现函数的优化
语法规则:
x = ga(fitnessfcn,nvars)x = ga(fitnessfcn,nvars,A,b)x = ga(fitnessfcn,nvars,A,b,Aeq,beq)x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)%
其中fitnessfc为函数的句柄或者为匿名函数
nvars,表示自变量个个数(例如自变量为向量X,nvars代表X中的元素个数)
A,b就是表达式A*X<=b;
Aeq:表示线性等式约束矩阵,若是没有等式约束就写为[];
Beq:表示线性等式约束的个数Beq=length(nvars);
2.1.1 f(x)=x+10sin(5x)+7cos(4x)
2.1.1.1 函数图像:
x = 0:0.01:25;
y = x+10*sin(5*x)+7*cos(4*x);
plot(x,y)
2.1.1.2 适应度函数:
function y = f1(x)
y = -(x+10*sin(5*x)+7*cos(4*x));
end
2.1.1.3 使用ga函数求解最大值:
x = 0:0.01:20;
y = x+10*sin(5*x)+7*cos(4*x);
plot(x,y)
hold on
OF = @f1;
nvars = 1;
LB = -20;
UB = 20;
[x,fval] = ga(OF,nvars,[],[],[],[],LB,UB)
plot(x,-fval,'*')
2.1.2 
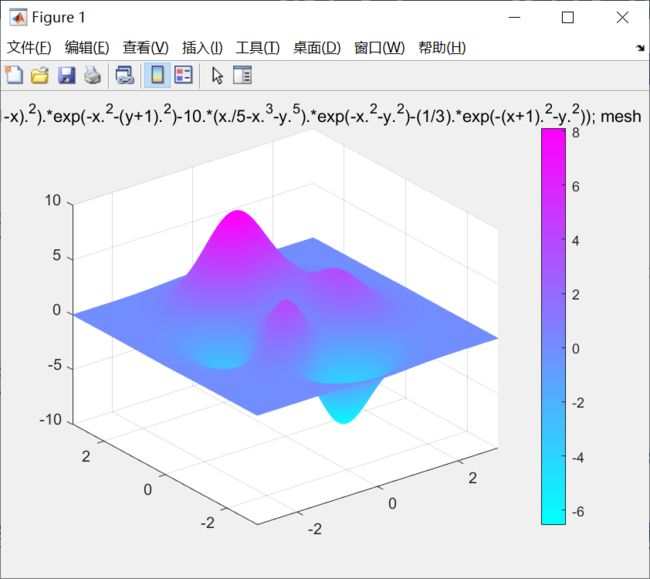
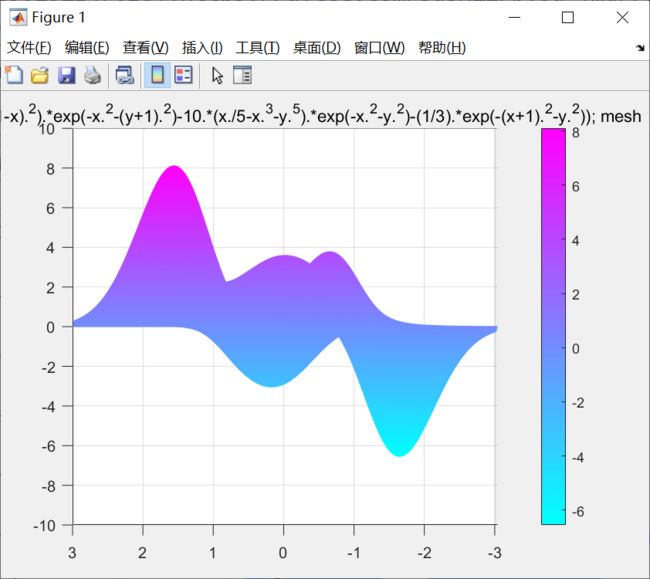
2.1.2.1 函数图像:
t=-3:.01:3;
[x,y]=meshgrid(t);%形成格点矩阵
z=-f2(x,y);
figure(1)
mesh(x,y,z);
axis([-3 3 -3 3 -10 10]);
title('z = (3.*((1-x).^2).*exp(-x.^2-(y+1).^2)-10.*(x./5-x.^3-y.^5).*exp(-x.^2-y.^2)-(1/3).*exp(-(x+1).^2-y.^2)); mesh')
colormap cool%cool是一种配色方案,还有其他方案如winter,summer····见help colormap
colorbar
2.1.2.2 适应度函数:
function z = f2(x)
z = -(3*((1-x(1))^2)*exp(-x(1)^2-(x(2)+1)^2)-10*(x(1)/5-x(1)^3-x(2)^5).*exp(-x(1)^2-x(2)^2)-(1/3)*exp(-(x(1)+1)^2-x(2)^2));
end
2.1.2.3 使用ga函数求解最大值:
f = @(x) 3*((1-x(1))^2)*exp(-x(1)^2-(x(2)+1)^2)-10*(x(1)/5-x(1)^3-x(2)^5)*exp(-x(1)^2-x(2)^2)-(1/3)*exp(-(x(1)+1)^2-x(2)^2);
nvars = 2;
lb = [-3; -3]; % x y的下限
ub = [3; 3] ; % x y的上限
[x,fval] = ga(f,nvars,[],[],[],[],lb,ub)
2.2 图形用户界面下应用遗传算法求解优化问题:
2.2.1 f(x)=x+10sin(5x)+7cos(4x)
2.2.2 
三、运行结果
3.1 利用matlab工具箱函数命令实现函数的优化
3.1.1 f(x)=x+10sin(5x)+7cos(4x)
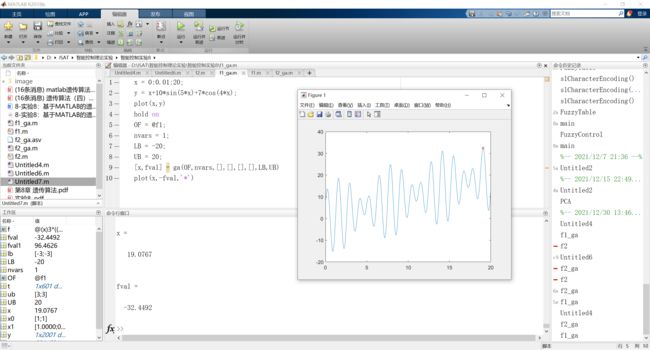
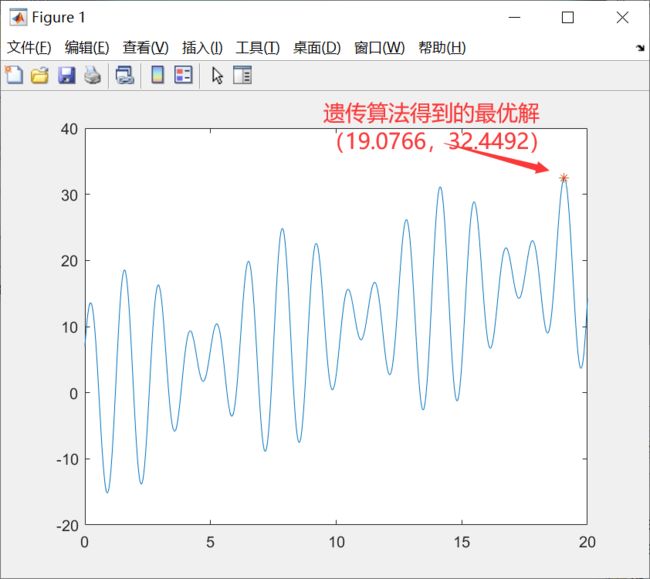
运行结果:
结果分析:
遗传算法很快得到了函数的最大值,但是并不是每次运行都能得到最优解,有时会陷入局部最大值中。
3.1.2 
运行结果:
结果分析:
根据图像观察,该二元函数的最大值大概在6~8之间,使用ga函数求解的最大值8.1062,符合要求。
3.2 图形用户界面下应用遗传算法求解优化问题:
3.2.1 f(x)=x+10sin(5x)+7cos(4x)
3.1.2 
四、总结:
(1)GA是对问题参数的编码(染色体)进行操作,而不是参数本身。
(2)GA计算简单,便于计算机编程,功能强。
(3)GA是从问题解的串集开始搜索,而不是从单个解开始,更有利于搜索到全局最优解。
(4)GA使用对象函数值(即适应值)这一信息进行搜索,而不需导数等其它信息。
(5)GA的复制、交叉、变异这三个算子都是由概率决定的,而非确定性的。
(6)GA算法具有隐含的并行性,因而可通过大规模并行计算来提高计算速度。
(7)GA更适合大规模复杂问题的优化,但解决简单问题效率并不高。