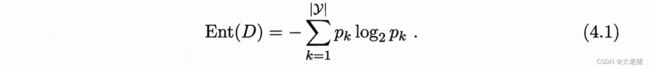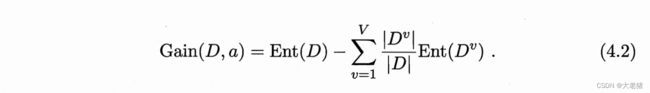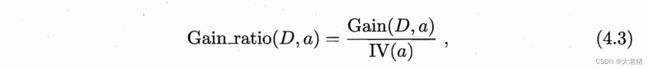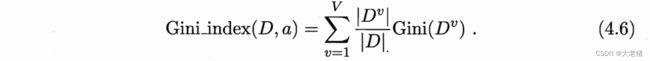机器学习_西瓜书_C4决策树
目录
4.1 算法原理
决策树结构
结点非可分: 递归
结点可分:MAX结点纯度purity(单结点同类别)
4.2 划分方法
ID3决策树 Iterative Dichotomiser 迭代二分器 (离散值)
C4.5决策树 (连续值)
CART决策树 Classification And Regression Tree
4.3 剪枝pruning, 连续值, 缺失值
预剪枝prepruning
后剪枝postpruning
连续值处理
缺失值处理
4.4 多变量决策树
Task2 学习心得
4.1 算法原理
决策树结构
- 根结点: 样本全集D
- 内部结点: 属性测试
- 叶结点: 结果
递归(Recursion): 在函数的定义中使用函数自身的方法. 自己调用自己, 有去有回.
https://zh.wikipedia.org/zh/%E9%80%92%E5%BD%92
先验分布: 抽样前认知;
后验分布: 抽样后认知, 联合条件概率=总体+样本+先验.
贝叶斯统计——先验分布与后验分布_东皇太乙的博客-CSDN博客_已知先验分布求后验分布
结点非可分: 递归
- 不用分: 结点内样本全为同一类别
- 无法分: (后验分布) 属性A=∅ or 所有属性的样本全部相同
- 不能分: (先验分布) 结点内样本为空
结点可分:MAX结点纯度purity(单结点同类别)
- ID3决策树
- C4.5决策树
- CART决策树
4.2 划分方法
ID3决策树 Iterative Dichotomiser 迭代二分器 (离散值)
衡量纯度指标
MIN 信息熵 info entropy ∈ [ 0 , log_2|y| ] 表示结果的不确定性,越小越好
MAX 信息增益 info gain 表示结果的收益性,越大越好
步骤
- 第一层: 好瓜/坏瓜
- all 单属性`gain = 根`熵 - 累计(单属性`熵)
- pick MAX(单属性`gain) 作为第二层 e.g.A4
- 第二层: A4
- all except A4 单属性`gain = A4`熵 - 累计(单属性`熵).
- pick MAX(单属性`gain) 作为第三层.
- repeat
评价
- 序号也可作为属性, 虽然info gain明显大于其他属性(∵单结点单样本,纯度max), 但是不具备泛化能力.
- info gain偏好可取纸数目多的属性, 直接使用不利
C4.5决策树 (连续值)
衡量纯度指标
增益率 gain ratio: 取代方法一info gain存在偏好的缺点
固有值 IV intrinsic value
评价
偏好可取值数目少的属性
非直接取MAX(gain ratio), 先find all 属性(ratio > AVG), 再 pick max
CART决策树 Classification And Regression Tree
衡量纯度指标
MIN 基尼值: 随机抽2样,类别不一致的概率,越小越好
描述数据集D
MIN 基尼指数 Gini index
描述属性a
4.3 剪枝pruning, 连续值, 缺失值
防止分支过多,过度拟合
预剪枝prepruning
划分前: 不能提升泛化性, 停止划分, 标记为叶结点end
判定能否提升泛化性: 使用C1性能评估方法, e.g.留出法
步骤
- 确认使用留出法, 随机选出验证集
- 选择属性, 基于max info gain, e.g."脐部"
- 标记训练集分类: 好瓜in凹陷TTTF→T, 稍凹TTFF→T*, 平坦FF→F (*标记某结点的类别时, 用样例中最多的那个类别, 一样多就任选)
- 匹配验证集分类: 凹凹稍稍平平凹, 按训练集标记为TTTTFFT, 实际TTTFFFF, 一致率5/7
- 判断是否执行划分: 算验证集精度(分类正确率), 划分后>前, 执行
- 第一层(划分前) 好瓜T/坏瓜F: 验证集精度 = 3/7 = 42.9%
- 第二层(划分后) 属性1脐部: 验证集精度 = 5/7 = 71.4% > 划分前42.9%
- 执行用"脐部"划分
- repeat
- 选择属性1-1, 基于max info gain, "脐部-凹陷"-色泽
- 标记训练集分类: 脐部-凹陷in绿T→T, 黑TT→T, 白F→F,
- 匹配验证集分类: 绿白绿, 按训练集标记为TFT, 实际TTF, 一致率2/3
- 判断是否执行划分:
- 第二层(划分前) 属性1脐部: 验证集精度 = 71.4%
- 第三层(划分后) "脐部-凹陷"-色泽: 验证集精度 = 57.1% < 划分前71.4%
- 不执行"脐部-凹陷"划分
- repeat
- 选择属性1-2, 基于max info gain, "脐部-稍凹"-根蒂
- ...划分后71.4% = 划分前, 不执行
- repeat
- 选择属性1-3, "脐部-平坦", 训练集样例分类一致, 不执行划分
评价
优: -过拟合风险; 减少训练/测试时间成本
缺: 剪掉的枝虽然当前不能提升泛化性,但其子分支未来可能提升; +欠拟合风险
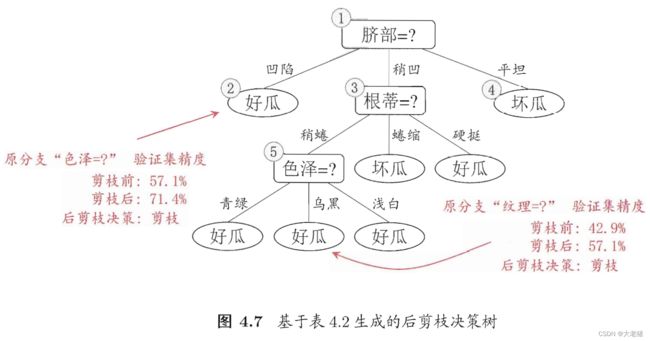
后剪枝postpruning
划分后: 自底向上检查整棵树的结点, 若有结点分支替换为叶结点能提升泛化性, 执行替换
步骤
- 求整个决策树的验证集精度
- 分支替换为叶结点, 标记叶结点, 求新验证集精度, >原:剪枝, <=原:不剪
评价
优: 比预剪枝保留更多分支; 欠拟合风险小; 泛化性能优于预剪枝
缺: 时间成本高
连续值处理
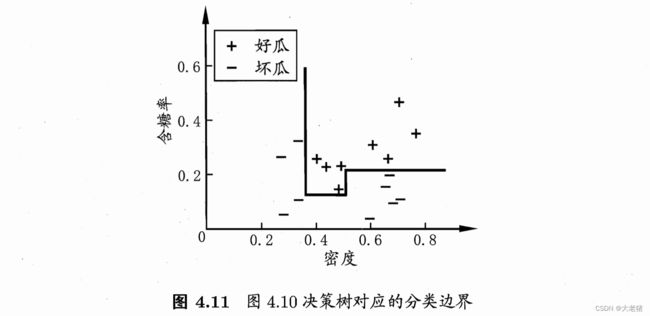
二分法bi-partition: 将连续属性离散化, applied in C4.5决策树算法
注意: 当前结点按连续属性划分, 子结点还可以继续按连续属性划分
步骤
- 将连续属性值从小到大排序
- 求info gain 和 划分点t, 按t划分集合D为Dt-和Dt+
- pick MAX(all info-gain)
- 递归划分
缺失值处理
问题1: 缺失属性值, 如何选择划分属性?
解决1: 根据D~判断属性优劣, D~: D在属性a上无缺失值的样本子集
问题2: 给定划分属性, 缺失样本值, 如何划分样本?
解决2 : 若属性a下样本值x已知, 将样本值x划入对应子结点, 样本权值w保持; 若未知, 将样本值x划入所有子结点, 权值调整为 r~*w. applied in C4.5决策树算法.
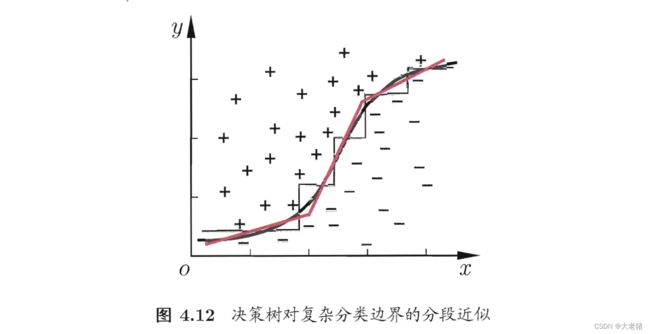
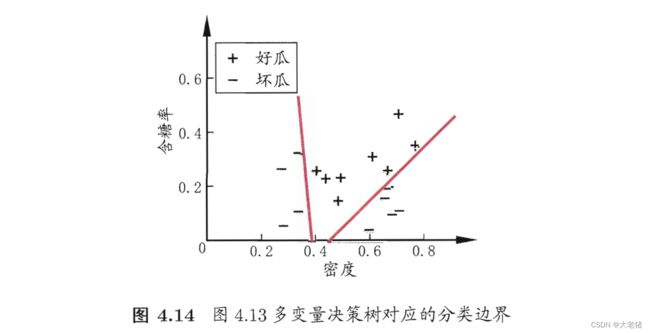
4.4 多变量决策树
单变量决策树uni-variate decision tree: 轴平行axis-parallel
多变量决策树multi-variate decision tree: 非叶结点不是仅针对某个属性,而是针对属性的线性组合
Task3 学习心得
- 理论: C4决策树相对简单, 学起来比C3轻松
- 代码: 在看吴恩达的ML和之前上课的课件
- datawhale的视频看完我还要来更新下笔记