人工神经网络—多层神经网络
多层神经网络
- 1. 回顾
- 2. 多层神经网络结构
-
- 2.1 两层神经网络例子
- 2.2 非线性函数的作用
- 3. 三层神经网络可以模拟任意的非线性函数
-
- 3.1 构造三角形非线性函数的神经网络结构
- 3.2 构造四边形非线性函数的神经网络结构
- 3.3 构造不规则封闭曲线非线性函数的神经网络结构
- 3.4 构造两个三角形非线性函数的神经结构
- 4. 结尾
- 参考资料
1. 回顾
在上一讲中,我们提到从上个世纪80年代开始,人工神经网络领域迎来了新的突破,产生了多层神经网络,人们终于可以利用人工神经网络处理非线性问题了。
2. 多层神经网络结构
2.1 两层神经网络例子
这一讲主要介绍多层神经网络的结构。下面这幅图是最简单的多层神经网络,它包含2层,总共由3个神经元相互连接而成。
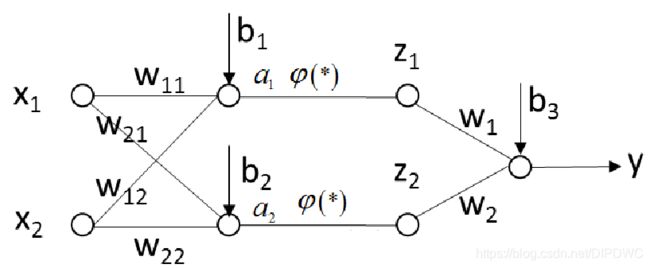
输入 X X X向量,有两个分量 x 1 x_1 x1, x 2 x_2 x2,输出 y y y是一个数值。我们逐层写出输入到输出之间的关系:
a 1 = ω 11 x 1 + ω 12 x 2 + b 1 a_1=ω_{11}x_1+ω_{12}x_2+b_1 a1=ω11x1+ω12x2+b1(第一个神经元)
a 2 = ω 21 x 1 + ω 22 x 2 + b 2 a_2=ω_{21}x_1+ω_{22}x_2+b_2 a2=ω21x1+ω22x2+b2(第二个神经元)
z 1 = φ ( a 1 ) z_1=φ(a_1) z1=φ(a1)(非线性函数)
z 2 = φ ( a 2 ) z_2=φ(a_2) z2=φ(a2)(非线性函数)
y = ω 1 z 1 + ω 2 z 2 + b 3 y=ω_1z_1+ω_2z_2+b_3 y=ω1z1+ω2z2+b3(第三个神经元)
当然,我们也可以用一个非常复杂的公式描述多层神经网络输入与输出的关系
y = w 1 φ ( ω 11 x 1 + ω 12 x 2 + b 1 ) + w 2 φ ( ω 21 x 1 + ω 22 x 2 + b 2 ) + b 3 (1) y=w_1φ(ω_{11}x_1+ω_{12}x_2+b_1)+w_2φ(ω_{21}x_1+ω_{22}x_2+b_2)+b_3\tag{1} y=w1φ(ω11x1+ω12x2+b1)+w2φ(ω21x1+ω22x2+b2)+b3(1)
这个神经网络分成了两层,第一层是前2个神经元,第二层是后一个神经元,两层之间用非线性函数 φ ( ∗ ) φ(*) φ(∗)连接起来。
这里有个问题请大家思考一下,在这个多层神经网络模型中,待求的参数是哪些呢?
显然,待求的参数有9个,分别是:
- 第一层网络中的( w 11 , w 12 , w 21 , w 22 , b 1 , b 2 w_{11},w_{12},w_{21},w_{22},b_1,b_2 w11,w12,w21,w22,b1,b2)
- 第二层网络中的( w 1 , w 2 , b 3 w_1,w_2,b_3 w1,w2,b3)
2.2 非线性函数的作用
需要强调的是两层之间的非线性函数 φ ( ∗ ) φ(*) φ(∗)是必须的。我们不妨考虑一下,如果我们不加这个非线性函数 φ ( ∗ ) φ(*) φ(∗),而是让第一层的输出直接作用到第二层的输入上会有什么结果呢?
这时输出 y y y将等于如下这个式子
y = w 1 ( ω 11 x 1 + ω 12 x 2 + b 1 ) + w 2 ( ω 21 x 1 + ω 22 x 2 + b 2 ) + b 3 y=w_1(ω_{11}x_1+ω_{12}x_2+b_1)+w_2(ω_{21}x_1+ω_{22}x_2+b_2)+b_3 y=w1(ω11x1+ω12x2+b1)+w2(ω21x1+ω22x2+b2)+b3
把它经过一系列的化简后
y = ( w 1 ω 11 + w 2 ω 21 ) x 1 + ( w 1 ω 12 + w 2 ω 22 ) x 2 + ( w 1 b 1 + w 2 b 2 + b 3 ) (2) y=(w_1ω_{11}+w_2ω_{21})x_1+(w_1ω_{12}+w_2ω_{22})x_2+(w_1b_1+w_2b_2+b_3)\tag{2} y=(w1ω11+w2ω21)x1+(w1ω12+w2ω22)x2+(w1b1+w2b2+b3)(2)
可以看到, y y y是 x 1 x_1 x1, x 2 x_2 x2加权求和再加上偏置的形式,输出仍然是输入的线性加权求和再加偏置的形式。
那么将有
y = w 1 x 1 + w 2 x 2 + b (3) y=w_1x_1+w_2x_2+b\tag{3} y=w1x1+w2x2+b(3)
综合上述复杂的式(2)及简单的式(3),我们可以看到,如果式(3)的 w 1 = w 1 ω 11 + w 2 ω 21 w_1=w_1ω_{11}+w_2ω_{21} w1=w1ω11+w2ω21,同时另外两个相应的式子也相应的相等,那么式(2)与式(3)将会是同一个模型。也就是说,如果层与层之间不加非线性函数,那么多层神经网络将会退化到一个神经元的感知器模型状态。
我们论证了在多层神经网络中必须加入非线性函数,下一个问题是我们要加的非线性函数是什么呢 ?
这里先直接给出答案,非线性函数是阶跃函数。例如
φ ( x ) = { 1 , x > 0 0 , x < 0 φ(x)=\begin{cases} 1, & x>0\\ 0, & x<0 \end{cases} φ(x)={1,0,x>0x<0
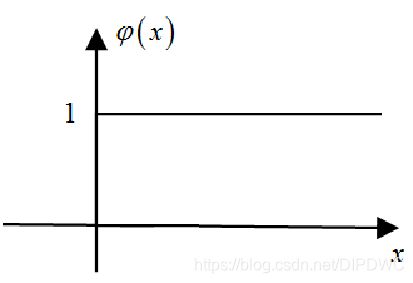
为什么要用阶跃函数作为多层神经网络的非线性函数呢?
因为有一个定理,如果非线性函数采用阶跃函数,那么三层神经网络可以模拟任意的非线性函数。
3. 三层神经网络可以模拟任意的非线性函数
在证明这个定理之前,我们来看一下多层神经网络的结构。我们可以任意的增加神经网络的层数,同时对于每一层我们可以任意的设置这一层神经元的个数,运用前面讲述的连接方式,我们将获得更大的神经网络。例如在如下图4所示的神经网络中,总共有3层,第一层有3个神经元,第二层有2个神经元,第三层有2个神经元,层与层之间用非线性函数连接。
接下来我们可以给出3层神经网络模拟任意非线性函数的证明了。
在这里我们假设特征空间是二维的,同时我们假设是二分类问题。对于特征空间大于二维,类别数大于两类的情况,证明的思路也是一样的。
3.1 构造三角形非线性函数的神经网络结构
首先,我们来看一个简单的非线性函数。在特征空间上,有一个三角形,在三角形内部的区域属于一类,而在三角形外部的区域属于另一类,如下图所示。
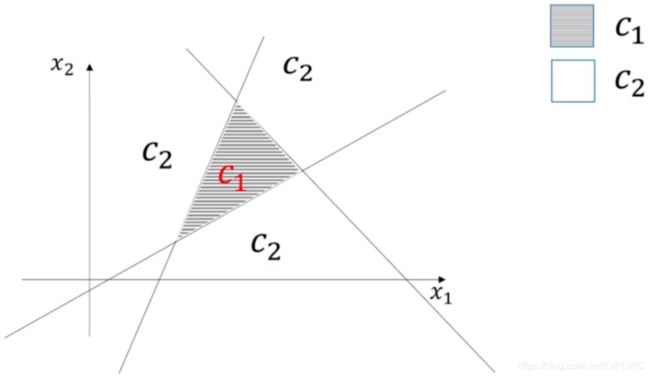
我们要用多层神经网络来构造一个函数使得:
如果 x x x在三角形内部,则输出 y > 0 y>0 y>0;
如果 x x x在三角形外部,则输出 y < 0 y<0 y<0。
怎么做呢?首先我们假定这个三角形三条边的方程分别是
{ w 11 x 1 + w 12 x 2 + b 1 = 0 w 21 x 1 + w 22 x 2 + b 2 = 0 w 31 x 1 + w 32 x 2 + b 3 = 0 \begin{cases} w_{11}x_1+w_{12}x_2+b_1=0\\ w_{21}x_1+w_{22}x_2+b_2=0\\ w_{31}x_1+w_{32}x_2+b_3=0 \end{cases} ⎩⎪⎨⎪⎧w11x1+w12x2+b1=0w21x1+w22x2+b2=0w31x1+w32x2+b3=0

同时我们假定上述三个方程中,在朝向三角形的一侧,其方程的值大于0;而远离三角形的一侧,其方程的值小于0。这是一定可以做到的,因为如果做不到,只需要将 w w w和 b b b取相反数即可。
那么我们如何构造一个两层的神经网络来实现在三角形内输出大于0而三角形外输出小于0呢?
第一层有3个神经元,每个神经元的 w w w和 b b b的值分别对应着三角形每一条边的方程,如下图所示。这样如果一个二维向量 X X X,它的两个分量 x 1 x_1 x1, x 2 x_2 x2在三角形里面,那么三个神经元输出的 a 1 a_1 a1, a 2 a_2 a2, a 3 a_3 a3将都大于0。
经过阶跃函数过后,输出 Z 1 , Z 2 , Z 3 Z_1,Z_2,Z_3 Z1,Z2,Z3都将等于1。
φ ( x ) = { 1 , x > 0 0 , x < 0 φ(x)=\begin{cases} 1, & x>0\\ 0, & x<0 \end{cases} φ(x)={1,0,x>0x<0

另一方面,如果 X X X在三角形外,那么 a 1 a_1 a1, a 2 a_2 a2, a 3 a_3 a3至少有一个小于0。经过阶跃函数过后, Z 1 , Z 2 , Z 3 Z_1,Z_2,Z_3 Z1,Z2,Z3也至少有一个等于0。

根据上面的分析,我们在第2层,将 Z 1 , Z 2 , Z 3 Z_1,Z_2,Z_3 Z1,Z2,Z3对应的 w w w全设置为1,而将偏置 b b b设置为-2.5,则满足条件。
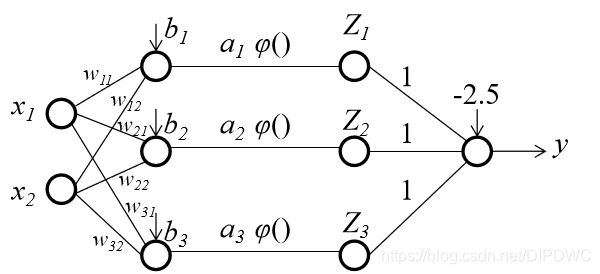
因为当且仅当 X X X在三角形内, Z 1 , Z 2 , Z 3 Z_1,Z_2,Z_3 Z1,Z2,Z3全为1,经过第2层神经元后,输出为y=0.5;而如果 X X X在三角形外, Z 1 , Z 2 , Z 3 Z_1,Z_2,Z_3 Z1,Z2,Z3不能全为1,至少有一个为0,经过第2层后,输出的y将会是一个负数,这样就达到了模拟这个非线性函数的目的。
3.2 构造四边形非线性函数的神经网络结构
下面我们假设特征空间有一个四边形,四边形里面属于一类,而四边形外面属于另一类,如下图所示。

我们如何做一个两层神经网络来区分这两类呢?有了前面的例子,这个问题很简单,只需要
- 在第一层增加一个神经元
- 第二层所有权重设置为1
- 偏置设置为-3.5
即可满足条件,可自行验证一下。
那么对于任意的多边形都可以采用这样的方法,所以两层神经网络足以模拟这样多边形的非线性函数。
3.3 构造不规则封闭曲线非线性函数的神经网络结构
接下来,如果有一个不规则的封闭曲线呢?例如下图所示,在圆圈里面是属于一类,而圆圈外面属于另一类。

我们能否用两层神经网络来模拟这样的非线性函数呢?虽然我们不能精确的获得这个非线性函数,但是我们却可以无限地逼近它。因为任何一个不规则的封闭曲线都可以用多边形去近似。例如我们可以用下面的绿色多边形去近似图上的圆圈,当多边形的边数趋近无限时,第二层神经元的个数也会趋于无限,这时我们可以以任意精度去逼近这个非线性函数。
3.4 构造两个三角形非线性函数的神经结构
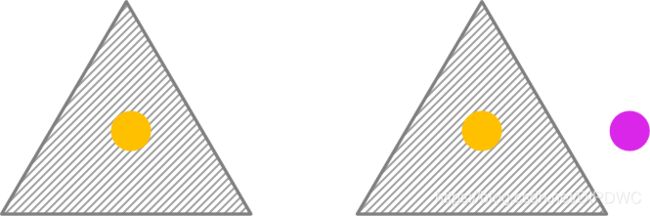
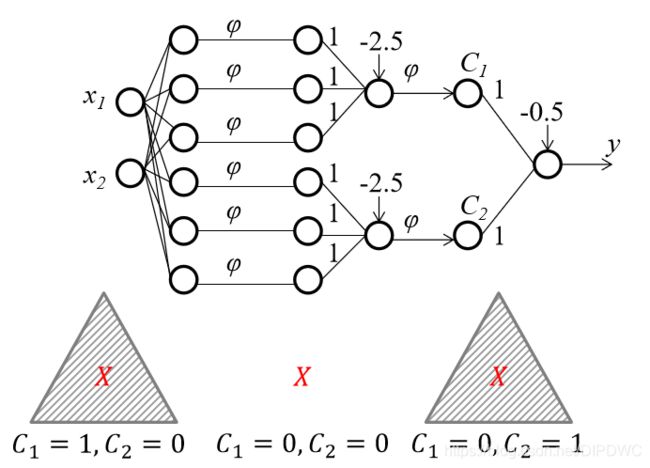
最后我们看一下,如果特征空间有2个三角形,如果 X X X处于两个三角形的任何一个当中,我们把它判定为同一类,而两个三角形的外面是另外一类。
答案是也是可以的。不过对于这个例子,我们需要用3层神经网络来模拟,如图所示。这个神经网络前面两层的设置都已经讲过,我们主要看最后一层,经过简单的推理可以得出,如果 X X X在第一个三角形里面,那么 C 1 = 1 , C 2 = 0 C_1=1,C_2=0 C1=1,C2=0;如果 X X X在第二个三角形里面,那么 C 1 = 0 , C 2 = 1 C_1=0,C_2=1 C1=0,C2=1;如果 X X X同时在两个三角形外面,那么 C 1 = 0 , C 2 = 0 C_1=0,C_2=0 C1=0,C2=0。因此只要最后一层将 C 1 , C 2 C_1,C2 C1,C2对应的权重都设置为1,而偏置 b b b设置为-0.5就可以区分 X X X在两个三角形内部还是在外部了,可自行验证一下。
学习了上面的知识,我们可以利用三层神经网络模拟任意的非线性二分类函数了。我们把特征空间上任意的区域设置为一类,再把另外的区域设置为另一类。请大家思考,按照上面的知识,如何设计三层神经网络来逼近这些函数呢?
4. 结尾
作为结尾,有两道思考题:
(1)假设非线性函数有三个取值的情况,例如特征空间中有两个三角形:
当向量 X X X在第一个三角形内时,y=2;
当向量 X X X在第二个三角形内时,y=1;
当向量 X X X在两个三角形外时,y=-1;
请设计一个三层神经网络来模拟这个非线性函数。
(2)如图所示,两条直线相交将特征空间分为四个区域,其中两个对角的区域(如阴影部分)属于同一类,而另两个对角区域(如白色部分)属于另一类。
- 请设计一个神经网络来模拟这个非线性函数。
- 请你深入思考一下,最少需要多少个神经元就能模拟这个非线性函数呢?
参考资料
- 浙江大学《机器学习》课程—胡浩基老师主讲
如果文章对你有帮助,请记得点赞与关注,谢谢!
![]()