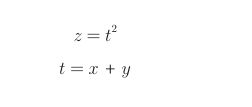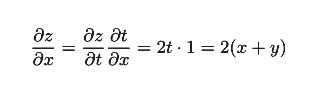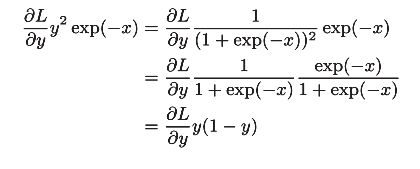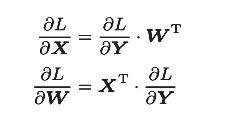深度学习入门之4--误差反向传播法
目录
1计算图
1.1计算图求解
1.2局部计算
2链式法则
2.1定义
2.2计算图的反向传播
2.3链式法则与计算图
3反向传播
3.1加法节点反向传播
3.2乘法节点反向传播
4简单层的实现
4.1乘法层的实现
4.2加法层的实现
5激活函数模块化
5.1Relu层
5.2Sigmoid层
5.3Affine层
5.3.1Affine层
5.3.2批版本的Affine层
5.4Softmax层
6误差反向传播案例
6.1common目录
6.1.1layers.py
6.1.2gradient.py
6.2ch05
6.2.1two_layer_net.py
6.2.2train_neuralnet.py
6.3结果
该文章是对《深度学习入门 基于Python的理论与实现》的总结,作者是[日]斋藤康毅
1计算图
1.1计算图求解
在上一篇中,使用的是数值微分计算参数的梯度(损失函数关于权重参数的梯度),但缺点是计算上比较费时,而误差反向传播则提高了效率。
误差反向传播法:1、基于数学式,2、基于计算图。第一种比较常见,在机器学习中都是以第一种方式使用的。对于计算图的方式,则可以使得表述更加易于让人理解。
例1:**在超市买了2个100日元一个的苹果,消费税是10%,请计算支付金额。
由上图,开始时,苹果的100日元流到“× 2”节点,变成200日元,然后被传递给下一个节点。接着,这个200日元流向“× 1.1”节点,变成220日元。因此,从这个计算图的结果可知,答案为220日元。
也可以写成另一种方式:
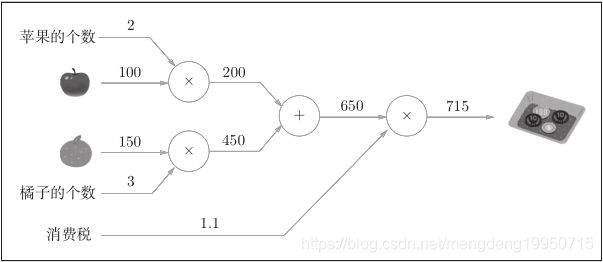
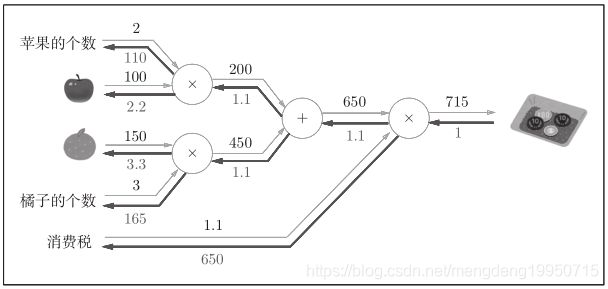
例2: XX在超市买了2个苹果、3个橘子。其中,苹果每个100日元,橘子每个150日元。消费税是10%,请计算支付金额。
计算图如下:
上图中新增了加法节点“+”,用来合计苹果和橘子的金额。构建了计算图后,从左向右进行计算。就像电路中的电流流动一样,计算结果从左向右传递。到达最右边的计算结果后,计算过程就结束了,答案为715日元。
则归纳上述步骤:
1.构建计算图。
2.在计算图上,从左向右进行计算(正向传播)。
1.2局部计算
通过上述的例子,可以知道,当计算时,除了苹果之外,还需要计算其他的水果,则:
1、计算图可以集中精力于局部计算
【注】当需要计算到苹果时,其它的无需关注
2、利用计算图可以将中间的计算结果全部保存起来(比如,计算进行到2个苹果时的金额是200日元、加上消费税之前的金额650日元等)。但是只有这些理由可能还无法令人信服。实际上,使用计算图最大的原因是,可以通过反向传播高效计算导数。
如和使用反向传播呢?
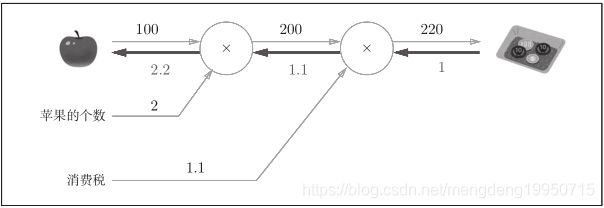
如图:
反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。由上图值,反向传
播从右向左传递导数的值(1 → 1.1 → 2.2)。
【注】计算图的优点:可以通过正向传播和反向传播高效地计算各个变量的导数值。
2链式法则
2.1定义
首先说一下复合函数,复合函数是由多个函数构成的函数。比如,z = (x + y) 2 ,当求z对x的偏导数时,将其它变量(y)看作常数。
使用换元得到下式:
则偏导数可以写成下面形式
2.2计算图的反向传播
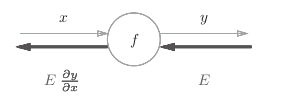
若y = f(x),则:
【注】反向传播的计算顺序是,将信号E乘以节点的局部导数![]() ,然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中y = f(x)的导数,也就是y关于x的导数
,然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中y = f(x)的导数,也就是y关于x的导数![]() 。一次计算下去,可以计算出梯度。
。一次计算下去,可以计算出梯度。
2.3链式法则与计算图
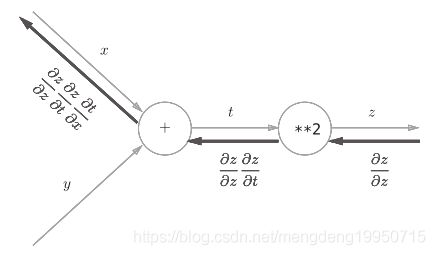
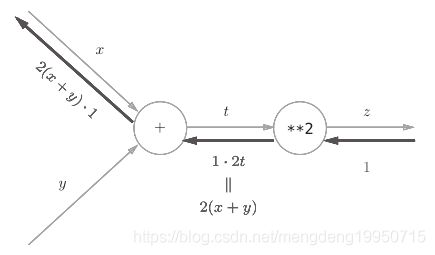
对于z = (x + y) 2,计算图如下:
【注】比如,反向传播时, “ ** 2 ”节点的输入是![]() ,则一直计算下去,便得到了正确的结果
,则一直计算下去,便得到了正确的结果
3反向传播
3.1加法节点反向传播
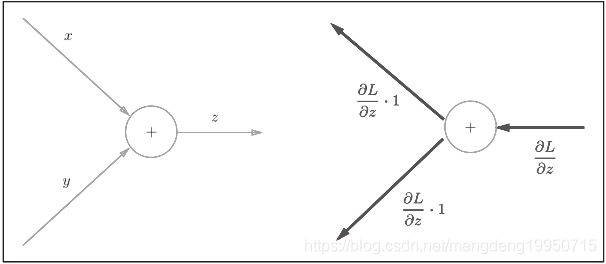
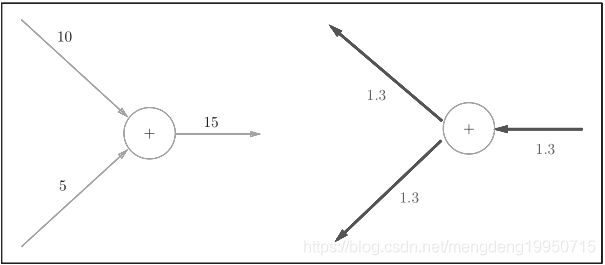
加法节点反向传播模式如下:
下面是一个例子,加法节点的反向传播将上游的值原封不动地输出到下游
3.2乘法节点反向传播
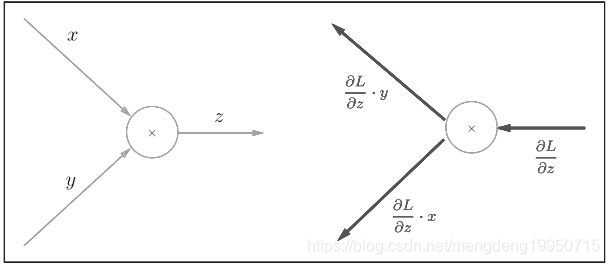
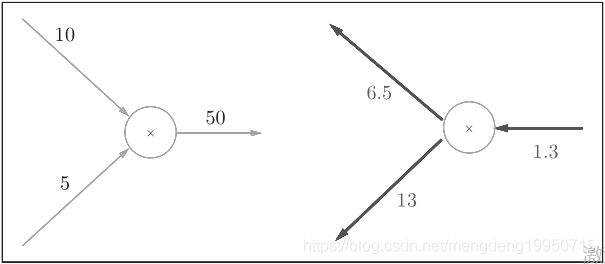
乘法节点反向传播模式如下:
【注】上图:1.3 * 5 = 6.5, 1.3 * 10 = 13
4简单层的实现
4.1乘法层的实现
乘法层图如下:
代码如下:
class MulLayer:
# 它们用于保存正向传播时的输入值。
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
if __name__ == "__main__":
apple = 100
apple_num = 2
tax = 1.1
# layer
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax) # 220.00000000000003
# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print(dapple, dapple_num, dtax) # 2.2 110.00000000000001 200
【注】在进行前向传播时,求梯度的参数会保存在初始化的对象中,用来进行反向传播
4.2加法层的实现
加法层例图如下:
代码实现如下:
class MulLayer:
# 它们用于保存正向传播时的输入值。
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
if __name__ == "__main__":
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1
# init
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
orange_price = mul_orange_layer.forward(orange, orange_num)
money = add_apple_orange_layer.forward(apple_price, orange_price)
mul_tax_price = mul_tax_layer.forward(money, tax)
# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice) # dtax = 650
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)
dapple, dapple_num = mul_apple_layer.backward(dapple_price) # 2.2 110.00000000000001
dorange, dorange_num = mul_orange_layer.backward(dorange_price) # 3.3000000000000003 165.0
print(dapple, dapple_num, dorange, dorange_num, dtax)
5激活函数模块化
函数的模块化,里面必须要有 forward()和 backward() ,且一般假定 forward()和 backward() 的参数是NumPy数组。
5.1Relu层
激活函数ReLU(Rectified Linear Unit)格式如下: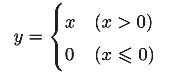
代码实现如下:
import numpy as np
from common.functions import softmax,cross_entropy_error
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0) # 保存的值时True或则False
out = x.copy()
out[self.mask] = 0 # 小于0的数赋值为0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
if __name__ == "__main__":
x = np.array([[1.0, -0.5], [-2.0, 3.0]])
'''
变量 mask 是由 True/False 构成的NumPy数组,它会把正向传播时的输入 x 的元素中
小于等于0的地方保存为 True ,其他地方(大于0的元素)保存为 False 。
'''
mask = (x <= 0)
# print(mask) # [[False True][ True False]]
out = x.copy()
# print(out) # [[ 1. -0.5][-2. 3. ]]
out[mask] = 0
# print(out) # [[1. 0.][0. 3.]]
# forward
re = Relu()
r1 = re.forward(x) # [[1. 0.][0. 3.]]
# backward
y = np.array([[1.0, 1.0], [1.0, 1.0]])
r2 = re.backward(y) # [[1. 0.][0. 1.]]
5.2Sigmoid层
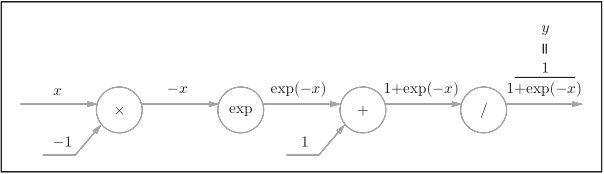
sigmoid函数如下:
【注】“exp”节点会进行y = exp(x)的计算,“/”节点会进行y=1/x 的计算。
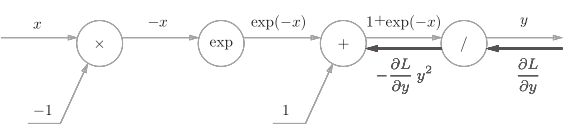
1、“/”节点表示y=1/x ,它的导数可以解析性地表示为下式。
反向传播时,会将上游的值乘以−y 2 (正向传播的输出的平方乘以−1后的值)后,再传给下游。如下图
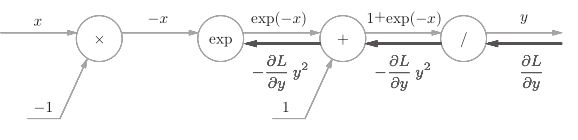
2、“+”节点将上游的值原封不动地传给下游。
3、“exp”节点表示y = exp(x),它的导数由下式表示。
计算图中,上游的值乘以正向传播时的输出(这个例子中是exp(−x))后,
再传给下游。
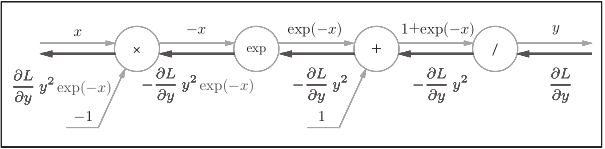
4、“×”节点将正向传播时的值翻转后做乘法运算。因此,这里要乘以−1。
得到下面的式子:
代码实现如下:
import numpy as np
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1/(1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
if __name__ == "__main__":
x = np.array([[1.0, -0.5], [-2.0, 3.0]])
y = np.array([[1.0, 1.0], [1.0, 1.0]])
sig = Sigmoid()
# forward
r1 = sig.forward(x) # [[0.73105858 0.37754067][0.11920292 0.95257413]]
# backward
r2 = sig.backward(y) # [[0.19661193 0.23500371][0.10499359 0.04517666]]
5.3Affine层
5.3.1Affine层
神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算(NumPy中是 np.dot() )
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”
【注】计算时,矩阵的维数必须正确
【注】注意变量是多维数组。反向传播时各个变量的下方标记了该变量的形状,求导不改变原矩阵维数
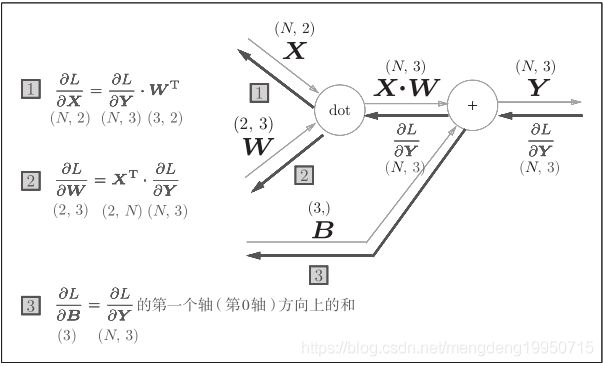
如图:
【注】X开始为2维数组,求导之后仍为2维数组
5.3.2批版本的Affine层
批版本的Affi ne层的计算图如下:
【注】反向传播时注意矩阵的维度的变化,正向传播时,偏置被加到X·W的各个数据上。因此,反向传播时,各个数据的反向传播的值需要汇总为偏置的元素。
代码实现如下:
import numpy as np
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
if __name__ == "__main__":
x = np.array([1.3, 2.0])
w = np.array([[1.0, -0.5, 1.5], [-2.0, 3.0, 1.0]])
b = np.array([1.0, 1.0, 1.0])
y = np.array([[0.1, 0.1, 0.1], [0.2, 0.1, 0.3]])
A = Affine(w, b)
r1 = A.forward(x) # [-1.7 6.35 4.95]
r2 = A.backward(y) # [[0.2 0.2][0.6 0.2]]
# m = np.array([1, 2])
# n = np.array([[1, 2, 3], [2, 3, 4]])
# print(np.dot(m.T, n)) # [ 5 8 11]
# print(np.dot(m, n)) # [ 5 8 11]
5.4Softmax层
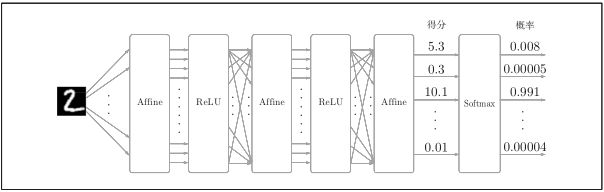
输出层的softmax函数,在前面提到过,softmax函数会将输入值正规化之后再输出,比如手写数字识别时,Softmax层的输出如
图所示。
包含作为损失函数的交叉熵误差(cross entropy error),所以称为“Softmax-with-Loss层”。
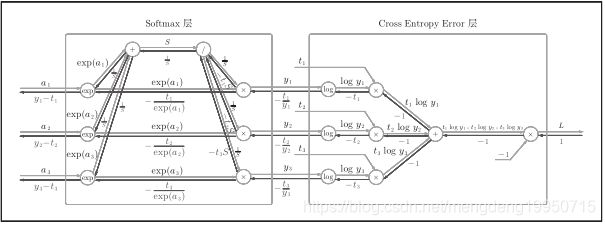
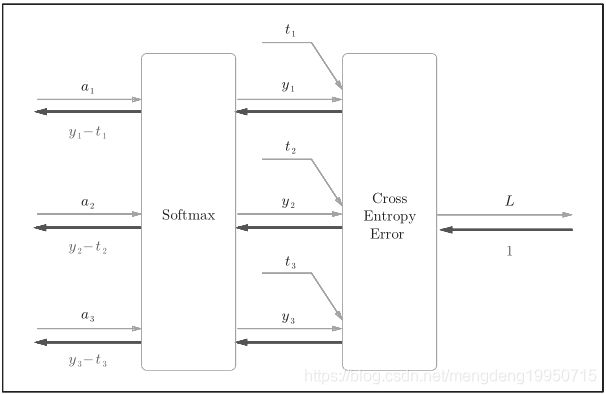
Softmax-with-Loss层的计算图:
【注】由上图,Softmax层将输入(a 1 , a 2 , a 3 )正规化,输出(y 1 ,y 2 , y 3 )。Cross Entropy Error层接收Softmax的输出(y 1 , y 2 , y 3 )和真实标签(t 1 ,t 2 , t 3 ),从这些数据中输出损失L。
上图的反向传播:Softmax层的反向传播得到了(y 1 − t 1 , y 2 − t 2 , y 3 − t 3 ),(y 1 − t 1 , y 2 − t 2 , y 3 − t 3 )是Softmax层的输出和真实标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层。
例如:真实标签是(0, 1, 0),Softmax层的输出是(0.3, 0.2, 0.5)的情形。因为正确解标签处的概率是0.2(20%),这个
时候的神经网络未能进行正确的识别。此时,Softmax层的反向传播传递的是(0.3, −0.8, 0.5)这样一个大的误差。
代码实现:
import numpy as np
# 输出层的激活函数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x)/np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x, axis=0)
return np.exp(x)/np.sum(np.exp(x))
# 交叉熵误差
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if y.size == t.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7))/batch_size
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 损失
self.y = None # softmax输出
self.t = None # 监督数据
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t)/batch_size
return dx
if __name__ == "__main__":
x = np.array([[0.6, 0.01], [0.4, 0.01]])
t = np.array([[1, 0], [0, 1]])
s = SoftmaxWithLoss()
# forward
r1 = s.forward(x, t) # 0.6740414156363213
# backward
r2 = s.backward() # [[-0.17831743 0.17831743][ 0.29814135 -0.29814135]]
6误差反向传播案例
手写数字识别文件目录:mnist.py省略
6.1common目录
functions.py已经省略,见上一篇
6.1.1layers.py
import numpy as np
from common.functions import softmax,cross_entropy_error
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 损失
self.y = None # softmax输出
self.t = None # 监督数据
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t)/batch_size
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1/(1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0 # 小于0的数赋值为0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
if __name__ == "__main__":
x = np.array([[1.0, -0.5], [-2.0, 3.0]])
mask = (x <= 0)
out = x.copy()
# out[mask] = 0
print(out)
6.1.2gradient.py
import numpy as np
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # 构造相同的维度
# 默认情况下,nditer将视待迭代遍历的数组为只读对象(read-only)
# 为了在遍历数组的同时,实现对数组元素值得修改,必须指定op_flags=['readwrite']模式:
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
# 对数组x进行行遍历
while not it.finished:
idx = it.multi_index # 索引
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2)/2*h
x[idx] = tmp_val
it.iternext()
return grad
if __name__ == "__main__":
# a = np.arange(6).reshape(2, 3)
a = np.array([[2, 1, 4], [6, 4, 10]])
# 单维迭代flags=['f_index'] 按照一维数组来显示
# 多维迭代flags=['multi_index'],显示二维数组的下标
# 列方式迭代 order='F', end='|'
# 行方式迭代 order='C', end='|'
it = np.nditer(a, flags=['f_index'], order='C')
while not it.finished:
print("<%s> %d" % (it.index, it[0]), end=' |')
# print("<%s> %d" % (it.multi_index, it[0]))
it.iternext()
6.2ch05
6.2.1two_layer_net.py
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1:
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t)/float(x.shape[0])
return accuracy
# x:输入数据,t:监督数据
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads
6.2.2train_neuralnet.py
import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from ch05.two_layer_net import TwoLayerNet
# 读取数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# 初始化网络
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000
train_size = x_train.shape[0] # 60000
batch_size = 100
learning_rate = 0.1
train_loss_list = [] # 训练误差
train_acc_list = [] # 训练精度
test_acc_list = [] # 测试精度
iter_per_epoch = max(train_size/batch_size, 1)
for i in range(iters_num): # 执行10000次
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask] # 得到一批图像
t_batch = t_train[batch_mask] # 得到一批图像的标签
# 通过误差反向传播法求梯度
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train_acc: "+str(train_acc)+" test_acc: "+str(test_acc))
# 绘图
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()6.3结果
运行结果如下:
得到的精度如下图:
由上图可知,通过误差反向传播得到的训练集的精度达到了97.885%,测试集精度达到了97.01%,比上一篇高了3个百分点。