[PKU 1127 1410 USTC 1121]判断线段相交 判断点在多边形内
{
Bloxorz的程序突然出现了bug
调试得郁闷
不过这也算是好事吧
先做了几道计算几何
学了2个基本的计算几何方法
}
计算几何有一个基本的问题
就是判断线段相交
这里介绍2种方法
一种是“外积”法 另一种是求交点
先讲"外积"法
这里的叉积好像有点不伦不类 说是外积吧 求出来却是一个纯量
说不是吧 又好像有外积求模的影子 似乎是外积的简化吧
不扯了 我就用*号代替×号好了
(本来计算机领域也是用*的 又能不混淆 两全其美)
这种运算针对2个向量(xp,yp) (xq,yq)
p*q=(xp,yp)*(xq,yq)=xp·yq-xq·yp 得到一个纯量A
这个P很能反映2个向量的关系
我们归纳出以下几个性质
p*q=-q*p 即*运算有方向性 q乘到p是不同与p乘到q的
A<0 则向量p在q的逆时针方向
A=0 则向量p与q共线
A>0 则向量p在q的顺时针方向
![[PKU 1127 1410 USTC 1121]判断线段相交 判断点在多边形内](http://img.e-com-net.com/image/product/e102b7ebf79748a181819e3b6705c0de.jpg)
这个性质让我们可以很好的判断线段和线段的位置关系
从而可以鉴别线段是否有跨立
我们认识到如果每条线段的2个端点分别在另一条线段的两侧
显然2条线段就相交了
我们称一条线段的2个端点分别在另一条线段的两侧称跨立
这就好比一个人两脚岔开 跨在一条白线两侧一样 很形象
那么 如何检测跨立呢?
我们用求*积解决
![[PKU 1127 1410 USTC 1121]判断线段相交 判断点在多边形内](http://img.e-com-net.com/image/product/51db73103143430b90d966bdbec7b4dc.jpg)
譬如判断l1对l2是否跨立
我们可以利用已知线段的端点 构造3个向量p q r
显然我们只需要判断p q是否分别在r两测即可
即判断(p*r)*(r*q)是否是正的 如果为正就可以判定跨立
如果为负就可以判定不跨立
一旦两次都判断跨立 则线段相交
讲到这里 我们还遗留有问题
如果线段的公共点是端点怎么办? 如果线段共线怎么办?
其实这就是(p*r)*(r*q)=0的情况 我们进行跨立试验的不足之处
我们还要引入快速排斥试验
正如其名 快速排斥好理解的多
只要判定分别以两线段为对角线的矩形是否相交
如果不相交必然线段也不相交
如果相交 则继续进行跨立试验
如果求出值为零 由于已经通过快速排斥试验 必然是有公共点的
也就可以直接判断了
判断矩形相交只需满足下图的条件即可
![[PKU 1127 1410 USTC 1121]判断线段相交 判断点在多边形内](http://img.e-com-net.com/image/product/7c7e44ea311e4ab8b230a7782f4fa638.png)
这样我们完成了"外积"法判断的全过程
给出代码
1
var
xnp,xmq,xnq,xmp,ynp,ymq,ynq,ymp,
2
xp1,yp1,xp2,yp2,xq1,yq1,xq2,yq2:longint;
3
i,n:longint;
4
function
ifxy:boolean;
5
begin
6
if
xp1
<
xp2
then
begin
xnp:
=
xp1; xmp:
=
xp2
end
else
begin
xnp:
=
xp2; xmp:
=
xp1;
end
;
7
if
yp1
<
yp2
then
begin
ynp:
=
yp1; ymp:
=
yp2
end
else
begin
ynp:
=
yp2; ymp:
=
yp1;
end
;
8
if
xq1
<
xq2
then
begin
xnq:
=
xq1; xmq:
=
xq2
end
else
begin
xnq:
=
xq2; xmq:
=
xq1;
end
;
9
if
yq1
<
yq2
then
begin
ynq:
=
yq1; ymq:
=
yq2
end
else
begin
ynq:
=
yq2; ymq:
=
yq1;
end
;
10
if
(xnp
>
xmq)
or
(xnq
>
xmp)
or
(ynp
>
ymq)
or
(ynq
>
ymp)
then
exit(false);
11
ifxy:
=
(((xp1
-
xq1)
*
(yq2
-
yq1)
-
(xq2
-
xq1)
*
(yp1
-
yq1))
*
((xq2
-
xq1)
*
(yp2
-
yq1)
-
(xp2
-
xq1)
*
(yq2
-
yq1))
>=
0
)
12
and
(((xq1
-
xp1)
*
(yp2
-
yp1)
-
(xp2
-
xp1)
*
(yq1
-
yp1))
*
((xp2
-
xp1)
*
(yq2
-
yp1)
-
(xq2
-
xp1)
*
(yp2
-
yp1))
>=
0
);
13
end
;
14
begin
15
assign(input,
'
seg.in
'
); reset(input);
16
assign(output,
'
seg.out
'
); rewrite(output);
17
readln(n);
18
for
i:
=
1
to
n
do
19
begin
20
readln(xp1,yp1,xp2,yp2,xq1,yq1,xq2,yq2);
21
writeln(ifxy);
22
end
;
23
close(input); close(output);
24
end
.
还需要补充的一点是
我这里为了节约代码量 把判断正负的工作缩减为乘法
不过有时候会卡乘法 用乘法int64会爆界 要改成比较大小
接下来是交点法
名副其实 就是求交点 很好理解
得用一点解析几何的结论
比如 过2点 (x1,y1) (x2,y2)的直线
可以表示为 (y2-y1)x+(x1-x2)y+(y1-y2)x1+(x2-x1)y1=0
两条直线联立求2元一次方程组解即可
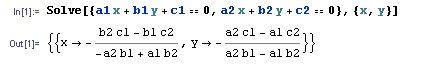
注意讨论有无解 是不是无数多解
还需注意除法的精度问题
1
var
x1,x2,x3,x4,y1,y2,y3,y4,i,n,
2
a1,a2,b1,b2,c1,c2:longint;
3
x0,y0:real;
4
function
max(a,b:longint):longint;
5
begin
6
if
a
>
b
then
max:
=
a
else
max:
=
b;
7
end
;
8
function
min(a,b:longint):longint;
9
begin
10
if
a
<
b
then
min:
=
a
else
min:
=
b;
11
end
;
12
function
d:boolean;
13
begin
14
a1:
=
y2
-
y1; b1:
=
x1
-
x2; c1:
=
(y1
-
y2)
*
x1
+
(x2
-
x1)
*
y1;
15
a2:
=
y4
-
y3; b2:
=
x3
-
x4; c2:
=
(y3
-
y4)
*
x3
+
(x4
-
x3)
*
y3;
16
if
(a1
*
b2
=
a2
*
b1)
17
then
if
(a1
*
c2
=
a2
*
c1)
18
then
exit(true)
19
else
exit(false)
20
else
begin
21
x0:
=-
(b2
*
c1
-
b1
*
c2)
/
(a1
*
b2
-
a2
*
b1);
22
y0:
=-
(a2
*
c1
-
a1
*
c2)
/
(a2
*
b1
-
a1
*
b2);
23
if
(min(x1,x2)
<=
x0)
and
(max(x1,x2)
>=
x0)
and
(min(x3,x4)
<=
x0)
and
(max(x3,x4)
>=
x0)
24
and
(min(y1,y2)
<=
y0)
and
(max(y1,y2)
>=
y0)
and
(min(y3,y4)
<=
y0)
and
(max(y3,y4)
>=
y0)
25
then
exit(true)
else
exit(false);
26
end
;
27
end
;
28
begin
29
assign(input,
'
seg.in
'
); reset(input);
30
assign(output,
'
seg0.out
'
); rewrite(output);
31
readln(n);
32
for
i:
=
1
to
n
do
33
begin
34
readln(x1,y1,x2,y2,x3,y3,x4,y4);
35
writeln(d);
36
end
;
37
close(input); close(output);
38
end
.
p.s.
有人说用了除法会慢 我测过数据了 没这个事
200w个询问 2种方法都是16s左右 耗时相当
不过第一种会爆界 第二种精度会不够 也算是各有千秋
要选择去用
我用这个基本方法解决了2个问题 都很裸
一个是pku 1127 需要+并查集 or Floyd 不难
另一个是pku 1410 注意矩形包含内部 不仅仅是边界
pku1127的代码
1
const
maxn
=
13
;
2
maxd
=
maxlongint shr
1
;
3
var
xnp,xmp,xnq,xmq,ynp,ymp,ynq,ymq,i,n,x,y,k,j:longint;
4
x1,x2,y1,y2:
array
[
1
..maxn]
of
longint;
5
f:
array
[
1
..maxn,
1
..maxn]
of
longint;
6
function
ifxy(i,j:longint):boolean;
7
begin
8
if
x1[i]
<
x2[i]
then
begin
xnp:
=
x1[i]; xmp:
=
x2[i];
end
else
begin
xnp:
=
x2[i]; xmp:
=
x1[i];
end
;
9
if
x1[j]
<
x2[j]
then
begin
xnq:
=
x1[j]; xmq:
=
x2[j];
end
else
begin
xnq:
=
x2[j]; xmq:
=
x1[j];
end
;
10
if
y1[i]
<
y2[i]
then
begin
ynp:
=
y1[i]; ymp:
=
y2[i];
end
else
begin
ynp:
=
y2[i]; ymp:
=
y1[i];
end
;
11
if
y1[j]
<
y2[j]
then
begin
ynq:
=
y1[j]; ymq:
=
y2[j];
end
else
begin
ynq:
=
y2[j]; ymq:
=
y1[j];
end
;
12
if
(xnp
>
xmq)
or
(xnq
>
xmp)
or
(ynp
>
ymq)
or
(ynq
>
ymp)
then
exit(false);
13
ifxy:
=
(((x1[i]
-
x1[j])
*
(y2[j]
-
y1[j])
-
(x2[j]
-
x1[j])
*
(y1[i]
-
y1[j]))
*
((x2[j]
-
x1[j])
*
(y2[i]
-
y1[j])
-
(x2[i]
-
x1[j])
*
(y2[j]
-
y1[j]))
>=
0
)
14
and
(((x1[j]
-
x1[i])
*
(y2[i]
-
y1[i])
-
(x2[i]
-
x1[i])
*
(y1[j]
-
y1[i]))
*
((x2[i]
-
x1[i])
*
(y2[j]
-
y1[i])
-
(x2[j]
-
x1[i])
*
(y2[i]
-
y1[i]))
>=
0
)
15
end
;
16
begin
17
assign(input,
'
jack.in
'
); reset(input);
18
assign(output,
'
jack.out
'
); rewrite(output);
19
readln(n);
20
while
n
<>
0
do
21
begin
22
for
i:
=
1
to
n
do
readln(x1[i],y1[i],x2[i],y2[i]);
23
for
i:
=
1
to
n
do
for
j:
=
1
to
n
do
if
ifxy(i,j)
then
f[i,j]:
=
1
else
f[i,j]:
=
maxd;
24
for
i:
=
1
to
n
do
f[i,i]:
=
0
;
25
for
k:
=
1
to
n
do
26
for
i:
=
1
to
n
do
27
for
j:
=
1
to
n
do
28
if
f[i,j]
>
f[i,k]
+
f[k,j]
then
f[i,j]:
=
f[i,k]
+
f[k,j];
29
readln(x,y);
30
while
x
<>
0
do
31
begin
32
if
f[x,y]
<
maxlongint shr
1
33
then
writeln(
'
CONNECTED
'
)
34
else
writeln(
'
NOT CONNECTED
'
);
35
readln(x,y);
36
end
;
37
readln(n);
38
end
;
39
close(input); close(output);
40
end
.
41
pku1410的代码
1
var
xnp,xmp,ynp,ymp,xnq,xmq,ynq,ymq,i,n,x1,x2,y1,y2,xp1,xp2,yp1,yp2:longint;
2
function
ifxy(xq1,yq1,xq2,yq2:longint):boolean;
3
begin
4
if
xp1
<
xp2
then
begin
xnp:
=
xp1; xmp:
=
xp2
end
else
begin
xnp:
=
xp2; xmp:
=
xp1;
end
;
5
if
yp1
<
yp2
then
begin
ynp:
=
yp1; ymp:
=
yp2
end
else
begin
ynp:
=
yp2; ymp:
=
yp1;
end
;
6
if
xq1
<
xq2
then
begin
xnq:
=
xq1; xmq:
=
xq2
end
else
begin
xnq:
=
xq2; xmq:
=
xq1;
end
;
7
if
yq1
<
yq2
then
begin
ynq:
=
yq1; ymq:
=
yq2
end
else
begin
ynq:
=
yq2; ymq:
=
yq1;
end
;
8
if
(xnp
>
xmq)
or
(xnq
>
xmp)
or
(ynp
>
ymq)
or
(ynq
>
ymp)
then
exit(false);
9
ifxy:
=
(((xp1
-
xq1)
*
(yq2
-
yq1)
-
(xq2
-
xq1)
*
(yp1
-
yq1))
*
((xq2
-
xq1)
*
(yp2
-
yq1)
-
(xp2
-
xq1)
*
(yq2
-
yq1))
>=
0
)
10
and
(((xq1
-
xp1)
*
(yp2
-
yp1)
-
(xp2
-
xp1)
*
(yq1
-
yp1))
*
((xp2
-
xp1)
*
(yq2
-
yp1)
-
(xq2
-
xp1)
*
(yp2
-
yp1))
>=
0
);
11
end
;
12
begin
13
assign(input,
'
inter.in
'
); reset(input);
14
assign(output,
'
inter.out
'
); rewrite(output);
15
readln(n);
16
for
i:
=
1
to
n
do
17
begin
18
readln(xp1,yp1,xp2,yp2,x1,y1,x2,y2);
19
if
x1
>
x2
then
begin
xnp:
=
x1; x1:
=
x2; x2:
=
xnp;
end
;
20
if
y1
>
y2
then
begin
xnp:
=
y1; y1:
=
y2; y2:
=
xnp;
end
;
21
if
(x1
<
xp1)
and
(xp1
<
x2)
and
(x1
<
xp2)
and
(xp2
<
x2)
and
(y1
<
yp1)
and
(yp1
<
y2)
and
(y1
<
yp2)
and
(yp2
<
y2)
or
22
(ifxy(x1,y1,x1,y2))
or
(ifxy(x1,y1,x2,y1))
or
(ifxy(x1,y2,x2,y2))
or
(ifxy(x2,y1,x2,y2))
23
then
writeln(
'
T
'
)
else
writeln(
'
F
'
);
24
end
;
25
close(input); close(output);
26
end
.
27
还有一个方法是判断点在多边形内部
一种方法是射线法 需要用到上面的判断线段相交
并且就是我说的爆界爆得利害的地方...
我们由点向外射一条射线 由于多边形是有界的
必然一部分在外边 我们沿着射线向内走
碰到一次边界说明我们从多边形外到了多边形内 或 从多边形内到了多边形外
显然这样改变的次数为奇数时 我们到达那个点时是在多边形内的即点在形内
![[PKU 1127 1410 USTC 1121]判断线段相交 判断点在多边形内](http://img.e-com-net.com/image/product/690d91fb6f404c8ba5d50bfdddbd4932.jpg)
这只是一个粗略的想法
还有很多细节需要注意
这里列出来
取射线可以取 垂直于坐标轴的射线 方便处理
射线其实就是另一端点很远的线段
这里由于线段的端点很大 很有可能在判断相交时爆界要注意
如果点在多边形边上直接特判
碰到与射线重合的边不予考虑
碰到与在射线上的点 如果是那条边上横坐标较大的点就计数 否则忽略
这样的需要扫描所有的边 复杂度是O(n)
还有很多方法譬如面积法 有兴趣可以去baidu
给出代码
1
const
maxn
=
50
;
2
inf
=
100000000
;
3
var
n,m,i,ans:longint;
4
x,y:
array
[
1
..maxn
+
1
]
of
longint;
5
xnp,xmq,xnq,xmp,ynp,ymq,ynq,ymp,x0,y0:int64;
6
function
ifxy(xp1,yp1,xp2,yp2,xq1,yq1,xq2,yq2:int64):boolean;
7
begin
8
if
xp1
<
xp2
then
begin
xnp:
=
xp1; xmp:
=
xp2
end
else
begin
xnp:
=
xp2; xmp:
=
xp1;
end
;
9
if
yp1
<
yp2
then
begin
ynp:
=
yp1; ymp:
=
yp2
end
else
begin
ynp:
=
yp2; ymp:
=
yp1;
end
;
10
if
xq1
<
xq2
then
begin
xnq:
=
xq1; xmq:
=
xq2
end
else
begin
xnq:
=
xq2; xmq:
=
xq1;
end
;
11
if
yq1
<
yq2
then
begin
ynq:
=
yq1; ymq:
=
yq2
end
else
begin
ynq:
=
yq2; ymq:
=
yq1;
end
;
12
if
(xnp
>
xmq)
or
(xnq
>
xmp)
or
(ynp
>
ymq)
or
(ynq
>
ymp)
then
exit(false);
13
ifxy:
=
(((xp1
-
xq1)
*
(yq2
-
yq1)
-
(xq2
-
xq1)
*
(yp1
-
yq1)
>=
0
)
and
((xq2
-
xq1)
*
(yp2
-
yq1)
-
(xp2
-
xq1)
*
(yq2
-
yq1)
>=
0
)
14
or
((xp1
-
xq1)
*
(yq2
-
yq1)
-
(xq2
-
xq1)
*
(yp1
-
yq1)
<=
0
)
and
((xq2
-
xq1)
*
(yp2
-
yq1)
-
(xp2
-
xq1)
*
(yq2
-
yq1)
<=
0
))
15
and
(((xq1
-
xp1)
*
(yp2
-
yp1)
-
(xp2
-
xp1)
*
(yq1
-
yp1)
>=
0
)
and
((xp2
-
xp1)
*
(yq2
-
yp1)
-
(xq2
-
xp1)
*
(yp2
-
yp1)
>=
0
)
16
or
((xq1
-
xp1)
*
(yp2
-
yp1)
-
(xp2
-
xp1)
*
(yq1
-
yp1)
<=
0
)
and
((xp2
-
xp1)
*
(yq2
-
yp1)
-
(xq2
-
xp1)
*
(yp2
-
yp1)
<=
0
));
17
end
;
18
function
ifp:longint;
19
var
i,j:longint;
20
begin
21
j:
=
0
;
22
for
i:
=
1
to
n
do
23
begin
24
if
ifxy(x0,y0,x0,y0,x[i],y[i],x[i
+
1
],y[i
+
1
])
then
exit(true);
25
if
x[i]
=
x[i
+
1
]
then
continue;
26
if
ifxy(x[i],y[i],x[i],y[i],x0,y0,x0,inf)
then
begin
if
x[i]
>
x[i
+
1
]
then
inc(j); continue;
end
;
27
if
ifxy(x[i
+
1
],y[i
+
1
],x[i
+
1
],y[i
+
1
],x0,y0,x0,inf)
then
begin
if
x[i
+
1
]
>
x[i]
then
inc(j); continue;
end
;
28
if
ifxy(x0,y0,x0,inf,x[i],y[i],x[i
+
1
],y[i
+
1
])
then
inc(j);
29
end
;
30
if
j
and
1
=
1
then
ifp:
=
true
else
ifp:
=
false;
31
end
;
32
begin
33
assign(input,
'
check.in
'
); reset(input);
34
assign(output,
'
check.out
'
); rewrite(output);
35
while
not
eof
do
36
begin
37
readln(n,m);
38
for
i:
=
1
to
n
do
readln(x[i],y[i]);
39
x[n
+
1
]:
=
x[
1
]; y[n
+
1
]:
=
y[
1
];
40
for
i:
=
1
to
m
do
41
begin
42
readln(x0,y0);
43
writeln(ifb);
44
end
;
45
end
;
46
close(input); close(output);
47
end
.
注意这里就对判断线段相交作了改动
我用这个方法解决了USTC 1121
题目也很裸 多边形内的点权为2 在外为1 求权和
我爆界爆了一个下午 哭...
1
const
maxn
=
50
;
2
inf
=
100000000
;
3
var
n,m,i,ans:longint;
4
x,y:
array
[
1
..maxn
+
1
]
of
longint;
5
xnp,xmq,xnq,xmp,ynp,ymq,ynq,ymp,x0,y0,x1,y1:int64;
6
function
ifxy(xp1,yp1,xp2,yp2,xq1,yq1,xq2,yq2:int64):boolean;
7
begin
8
if
xp1
<
xp2
then
begin
xnp:
=
xp1; xmp:
=
xp2
end
else
begin
xnp:
=
xp2; xmp:
=
xp1;
end
;
9
if
yp1
<
yp2
then
begin
ynp:
=
yp1; ymp:
=
yp2
end
else
begin
ynp:
=
yp2; ymp:
=
yp1;
end
;
10
if
xq1
<
xq2
then
begin
xnq:
=
xq1; xmq:
=
xq2
end
else
begin
xnq:
=
xq2; xmq:
=
xq1;
end
;
11
if
yq1
<
yq2
then
begin
ynq:
=
yq1; ymq:
=
yq2
end
else
begin
ynq:
=
yq2; ymq:
=
yq1;
end
;
12
if
(xnp
>
xmq)
or
(xnq
>
xmp)
or
(ynp
>
ymq)
or
(ynq
>
ymp)
then
exit(false);
13
ifxy:
=
(((xp1
-
xq1)
*
(yq2
-
yq1)
-
(xq2
-
xq1)
*
(yp1
-
yq1)
>=
0
)
and
((xq2
-
xq1)
*
(yp2
-
yq1)
-
(xp2
-
xq1)
*
(yq2
-
yq1)
>=
0
)
14
or
((xp1
-
xq1)
*
(yq2
-
yq1)
-
(xq2
-
xq1)
*
(yp1
-
yq1)
<=
0
)
and
((xq2
-
xq1)
*
(yp2
-
yq1)
-
(xp2
-
xq1)
*
(yq2
-
yq1)
<=
0
))
15
and
(((xq1
-
xp1)
*
(yp2
-
yp1)
-
(xp2
-
xp1)
*
(yq1
-
yp1)
>=
0
)
and
((xp2
-
xp1)
*
(yq2
-
yp1)
-
(xq2
-
xp1)
*
(yp2
-
yp1)
>=
0
)
16
or
((xq1
-
xp1)
*
(yp2
-
yp1)
-
(xp2
-
xp1)
*
(yq1
-
yp1)
<=
0
)
and
((xp2
-
xp1)
*
(yq2
-
yp1)
-
(xq2
-
xp1)
*
(yp2
-
yp1)
<=
0
));
17
end
;
18
function
ifp:longint;
19
var
i,j:longint;
20
begin
21
j:
=
0
;
22
for
i:
=
1
to
n
do
23
begin
24
if
ifxy(x0,y0,x0,y0,x[i],y[i],x[i
+
1
],y[i
+
1
])
then
exit(
1
);
25
if
x[i]
=
x[i
+
1
]
then
continue;
26
if
ifxy(x[i],y[i],x[i],y[i],x0,y0,x0,inf)
then
begin
if
x[i]
>
x[i
+
1
]
then
inc(j); continue;
end
;
27
if
ifxy(x[i
+
1
],y[i
+
1
],x[i
+
1
],y[i
+
1
],x0,y0,x0,inf)
then
begin
if
x[i
+
1
]
>
x[i]
then
inc(j); continue;
end
;
28
if
ifxy(x0,y0,x0,inf,x[i],y[i],x[i
+
1
],y[i
+
1
])
29
then
inc(j);
30
end
;
31
ifp:
=
j
and
1
;
32
end
;
33
begin
34
assign(input,
'
island.in
'
); reset(input);
35
assign(output,
'
island.out
'
); rewrite(output);
36
readln(n,m);
37
while
n
<>
0
do
38
begin
39
for
i:
=
1
to
n
do
40
readln(x[i],y[i]);
41
x[n
+
1
]:
=
x[
1
]; y[n
+
1
]:
=
y[
1
];
42
ans:
=
0
;
43
for
i:
=
1
to
m
do
44
begin
45
readln(x0,y0);
46
inc(ans); ans:
=
ans
+
ifp;
47
end
;
48
writeln(ans);
49
readln(n,m);
50
end
;
51
close(input); close(output);
52
end
.
53
计算几何代码都一坨一坨的
要有耐心 要注意常数 精度 爆界...