语音增强--卡尔曼滤波介绍及MATLAB实现
语音增强--------------卡尔曼滤波
状态方程
x k + 1 = Φ k x k + Γ u k {{\mathbf{x}}_{k+1}}={{\mathbf{\Phi }}_{k}}{{\mathbf{x}}_{k}}+\mathbf{\Gamma }{{\mathbf{u}}_{k}} xk+1=Φkxk+Γuk
观测方程
y k + 1 = H k + 1 x k + 1 + n k + 1 {{\mathbf{y}}_{k+1}}={{\mathbf{H}}_{k+1}}{{\mathbf{x}}_{k+1}}+{{\mathbf{n}}_{k+1}} yk+1=Hk+1xk+1+nk+1
原理介绍
假设在时刻 t k {{t}_{k}} tk,基于 t k {{t}_{k}} tk时刻以前所获得的全部知识,对状态变量 x k {{\mathbf{x}}_{k}} xk做出一个预测估计,记为 x ^ k − \mathbf{\hat{x}}_{k}^{-} x^k−,则预测估计的误差为
e k − = x k − x ^ k − \mathbf{e}_{k}^{-}={{\mathbf{x}}_{k}}-\mathbf{\hat{x}}_{k}^{-} ek−=xk−x^k−
称为预测误差。预测误差是零均值的,其协方差矩阵为
C k − = E { e k − e k − T } = E { ( x k − x ^ k − ) ( x k − x ^ k − ) T } \mathbf{C}_{k}^{-}=E\left\{ \mathbf{e}_{k}^{-}\mathbf{e}{{_{k}^{-}}^{T}} \right\}\left. =E\left\{ \left( {{\mathbf{x}}_{k}}-\mathbf{\hat{x}}_{k}^{-} \right){{\left( {{\mathbf{x}}_{k}}-\mathbf{\hat{x}}_{k}^{-} \right)}^{T}} \right. \right\} Ck−=E{ek−ek−T}=E{(xk−x^k−)(xk−x^k−)T}
在预测估计 x ^ k − \mathbf{\hat{x}}_{k}^{-} x^k−的基础上,利用 t k {{t}_{k}} tk时刻所获取的新观测数据 y k {{\mathbf{y}}_{k}} yk来进一步改善对 x k {{\mathbf{x}}_{k}} xk的估计,记为 x ^ k {{\mathbf{\hat{x}}}_{k}} x^k,称为更新估计,更新估计通过下式完成:
x ^ k = x ^ k − + K k ( y k − H k x ^ k − ) {{\mathbf{\hat{x}}}_{k}}=\mathbf{\hat{x}}_{k}^{-}+{{\mathbf{K}}_{k}}\left( {{\mathbf{y}}_{k}}-{{\mathbf{H}}_{k}}\mathbf{\hat{x}}_{k}^{-} \right) x^k=x^k−+Kk(yk−Hkx^k−)
其中 K k {{\mathbf{K}}_{k}} Kk为待定的增益矩阵,称为卡尔曼增益。
更新估计的误差记作 e k {{\mathbf{e}}_{k}} ek,则有
e k = x k − x ^ k = x k − [ x ^ k − + K k ( y k − H k x ^ k − ) ] {{\mathbf{e}}_{k}}={{\mathbf{x}}_{k}}-{{\mathbf{\hat{x}}}_{k}}={{\mathbf{x}}_{k}}-\left[ \mathbf{\hat{x}}_{k}^{-}+ \right.\left. {{\mathbf{K}}_{k}}\left( {{\mathbf{y}}_{k}}-{{\mathbf{H}}_{k}}\mathbf{\hat{x}}_{k}^{-} \right) \right] ek=xk−x^k=xk−[x^k−+Kk(yk−Hkx^k−)]
矢量卡尔曼滤波的实质就是寻找适当的增益矩阵 K k {{\mathbf{K}}_{k}} Kk,使更新估计的均方误差达到最小。
具体推导过程可以参照参考文献[1],这里只给出最终的递推过程
(1) 建立状态空间模型
x k + 1 = Φ k x k + Γ u k y k + 1 = H k + 1 x k + 1 + n k + 1 \begin{aligned} & {{\mathbf{x}}_{k+1}}={{\mathbf{\Phi }}_{k}}{{\mathbf{x}}_{k}}+\mathbf{\Gamma }{{\mathbf{u}}_{k}} \\ & {{\mathbf{y}}_{k+1}}={{\mathbf{H}}_{k+1}}{{\mathbf{x}}_{k+1}}+{{\mathbf{n}}_{k+1}} \\ \end{aligned} xk+1=Φkxk+Γukyk+1=Hk+1xk+1+nk+1
(2) 设置初始化条件
x ^ 0 = E { x 0 } C 0 = V a r { x 0 } \begin{aligned} & {{{\mathbf{\hat{x}}}}_{0}}=E\left\{ {{\mathbf{x}}_{0}} \right\} \\ & {{\mathbf{C}}_{0}}=Var\left\{ {{\mathbf{x}}_{0}} \right\} \end{aligned} x^0=E{x0}C0=Var{x0}
(3) 预测
x ^ k + 1 − = Φ k x ^ k \mathbf{\hat{x}}_{k+1}^{-}={{\mathbf{\Phi }}_{k}}{{\mathbf{\hat{x}}}_{k}} x^k+1−=Φkx^k
(4) 计算预测误差的协方差
C k + 1 − = Φ k C k Φ k T + Γ Q k Γ T \mathbf{C}_{k+1}^{-}={{\mathbf{\Phi }}_{k}}{{\mathbf{C}}_{k}}\mathbf{\Phi }_{k}^{T}+\mathbf{\Gamma }{{\mathbf{Q}}_{k}}{{\mathbf{\Gamma }}^{T}} Ck+1−=ΦkCkΦkT+ΓQkΓT
(5) 计算卡尔曼增益
K k + 1 = C k + 1 − H k + 1 T ( H k + 1 C k + 1 − H k + 1 T + R k + 1 ) − 1 {{\mathbf{K}}_{k+1}}=\mathbf{C}_{k+1}^{-}\mathbf{H}_{k+1}^{T}{{\left( {{\mathbf{H}}_{k+1}}\mathbf{C}_{k+1}^{-}\mathbf{H}_{k+1}^{T}+{{\mathbf{R}}_{k+1}} \right)}^{-1}} Kk+1=Ck+1−Hk+1T(Hk+1Ck+1−Hk+1T+Rk+1)−1
(6) 更新
x ^ k + 1 = x ^ k + 1 − + K k + 1 ( y k + 1 − H k + 1 x ^ k + 1 − ) {{\mathbf{\hat{x}}}_{k+1}}=\mathbf{\hat{x}}_{k+1}^{-}+{{\mathbf{K}}_{k+1}}\left( {{\mathbf{y}}_{k+1}}-{{\mathbf{H}}_{k+1}}\mathbf{\hat{x}}_{k+1}^{-} \right) x^k+1=x^k+1−+Kk+1(yk+1−Hk+1x^k+1−)
(7) 估计误差的协方差
C k + 1 = ( I − K k + 1 H k + 1 ) C k + 1 − {{\mathbf{C}}_{k+1}}=\left( \mathbf{I}-{{\mathbf{K}}_{k+1}}{{\mathbf{H}}_{k+1}} \right)\mathbf{C}_{k+1}^{-} Ck+1=(I−Kk+1Hk+1)Ck+1−
(8) 令 k = k + 1 k=k+1 k=k+1 ,重复步骤(3)-(8)直到当前时刻
其中
E { n k n i T } = { R k i = k 0 i ≠ k E\left\{ {{\mathbf{n}}_{k}}\mathbf{n}_{i}^{T} \right\}=\left\{ \begin{aligned} & {{\mathbf{R}}_{k}}\quad i=k \\ & 0\quad \ \ i\ne k \\ \end{aligned} \right. E{nkniT}={Rki=k0 i=k
E { u k u i T } = { Q k i = k 0 i ≠ k E\left\{ {{\mathbf{u}}_{k}}\mathbf{u}_{i}^{T} \right\}=\left\{ \begin{aligned} & {{\mathbf{Q}}_{k}}\ \ \ \text{ }i=k \\ & 0\ \ \ \ \text{ }i\ne k \\ \end{aligned} \right. E{ukuiT}={Qk i=k0 i=k
仿真参数为
| 参数名称 | 参数值 |
|---|---|
| 信噪比 | 5dB |
| 采样率 | 16KHz |
仿真结果如下
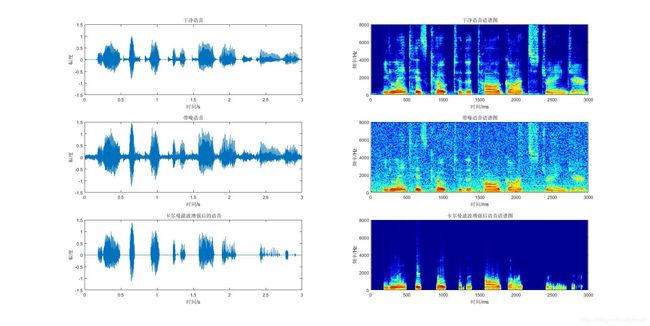
随着卡尔曼滤波收敛的过程中,误差的协方差矩阵会变得越来越小,从图中也可以看出,经过卡尔曼滤波之后的语音信号,噪声很大程度地被滤除,进一步地提高了语音的质量。
主函数
clear;
close all;
clc;
%% 读入数据
[signal,~]=audioread('clean.wav'); %读入干净语音
[noise,fs]=audioread('noise.wav'); %读入噪声
N=3*fs; %选取3秒的语音
signal=signal(1:N);
noise=noise(1:N);
t=(0:N-1)/fs;
SNR=5; %信噪比大小
noise=noise/norm(noise,2).*10^(-SNR/20)*norm(signal);
x=signal+noise; %产生固定信噪比的带噪语音
Time = (0:1/fs:(length(signal)-1)/fs)'; %时间轴
Noise=x(1:fs,1); %选取前1秒语音作为噪声方差估计
len_win = 0.0025; % 窗长2.5ms
shift_percent = 1; % 窗移占比
AR_order = 20; % 滤波器阶数
iter = 7; %迭代次数设置
%% 分帧加窗处理
len_winframe = fix(len_win * fs);
window = ones(len_winframe,1);
[y, num_frame] = KFrame(x, len_winframe, window, shift_percent);
%% 初始化
H = [zeros(1,AR_order-1),1]; % 观测矩阵
R = var(Noise); % 噪声方差
[filt_coeff, Q] = lpc(y, AR_order); % LPC预测,得到滤波器的系数
C = R * eye(AR_order,AR_order); % 误差协方差矩阵
enhanced_speech = zeros(1,length(x)); % 增强后的语音信号
enhanced_speech(1:AR_order) = x(1:AR_order,1)'; %初始化
updata_x = x(1:AR_order,1);
% 迭代器的次数.
i = AR_order+1;
j = AR_order+1;
%% 卡尔曼滤波
for k = 1:num_frame %一次处理一帧信号
jStart = j; %跟踪每次迭代AR_Order+1的值.
OutputOld = updata_x; %为每次迭代保留第一批AROrder预估量
for l = 1:iter %迭代次数
fai = [zeros(AR_order-1,1) eye(AR_order-1); fliplr(-filt_coeff(k,2:end))];
for ii = i:len_winframe
%% 卡尔曼滤波
predict_x = fai * updata_x;
predict_C = (fai * C * fai') + (H' * Q(k) * H);
K = (predict_C * H')/((H * predict_C * H') + R);
updata_x = predict_x + (K * (y(ii,k) - (H*predict_x)));
enhanced_speech(j-AR_order+1:j) = updata_x';
C = (eye(AR_order) - K * H) * predict_C;
j = j+1;
end
i = 1;
if l < iter
j = jStart;
updata_x = OutputOld;
end
% 更新滤波后信号的lpc
[filt_coeff(k,:), Q(k)] = lpc(enhanced_speech((k-1)*len_winframe+1:k*len_winframe),AR_order);
end
end
enhanced_speech = enhanced_speech(1:N)';
figure(1)
subplot(321);
plot(t,signal);ylim([-1.5,1.5]);title('干净语音');xlabel('时间/s');ylabel('幅度');
subplot(323);
plot(t,x);ylim([-1.5,1.5]);title('带噪语音');xlabel('时间/s');ylabel('幅度');
subplot(325);
plot(t,real(enhanced_speech));ylim([-1.5,1.5]);title('卡尔曼滤波增强后的语音');xlabel('时间/s');ylabel('幅度');
subplot(322);
spectrogram(signal,256,128,256,16000,'yaxis');
subplot(324);
spectrogram(x,256,128,256,16000,'yaxis');
subplot(326);
spectrogram(enhanced_speech,256,128,256,16000,'yaxis');
KFrame.m
function [Output, NumSegments] = KFrame(Input, WindowLength, Window, HoppingSize)
% Chopper windows the signal based on window length, shift percantage and
% uses Hamming windowing technique.
% Number of samples to hop.
HoppingSamples = fix(WindowLength.*HoppingSize);
% Number of segments.
NumSegments = fix(((length(Input)-WindowLength)/HoppingSamples) + 1);
% Index matrix which guides the signal through chopping process.
Index = (repmat(1:WindowLength,NumSegments,1) + repmat((0:(NumSegments-1))'*HoppingSamples,1,WindowLength))';
% Final window which multiplies with original signal to give pieces of it.
FinalWindow = repmat(Window,1,NumSegments);
% Ta-da...
Output = Input(Index).*FinalWindow;
end
关于语音及噪声文件,具体请参考:语音信号处理常用语料库下载地址
参考文献:
[1] 叶中付. 统计信号处理[M]. 中国科学技术大学出版社, 2013.