【机器学习】课程笔记11_支持向量机(Support Vector Machines)
支持向量机
- 优化目标(Optimization Objective)
- 大间距的直观理解(Large Margin Intuition)
- 大间距分类背后的数学(The Mathematics Behind Large Margin Classification)
- 核函数1(Kernels Ⅰ)
- 核函数2(Kernels Ⅱ)
- 使用支持向量机(Using An SVM)
优化目标(Optimization Objective)
-
支持向量机(Support Vector Machine, SVM): 使用简单函数来近似逻辑回归模型曲线,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
-
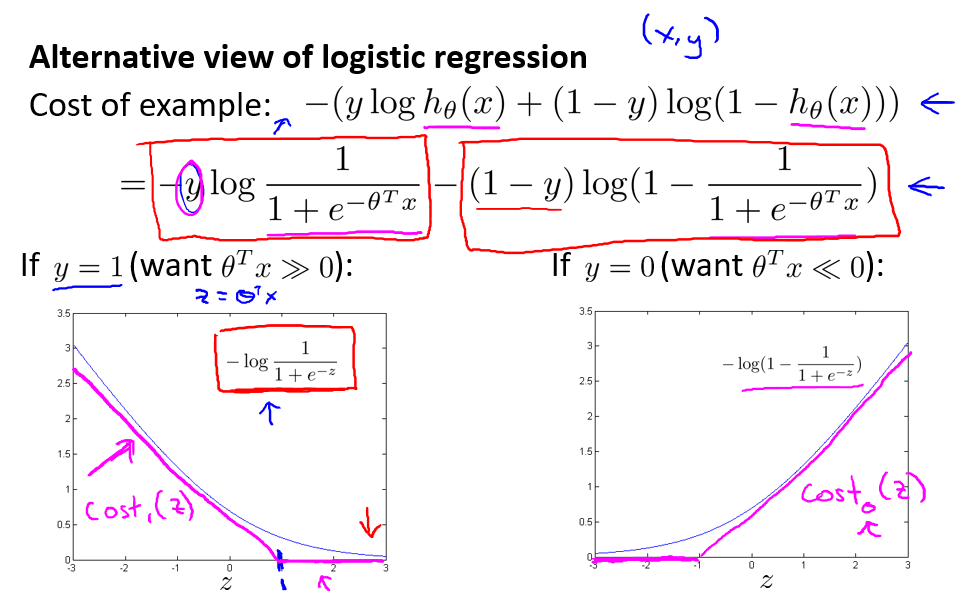
逻辑回归代价函数: J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) l o g ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=\cfrac{1}{m}\displaystyle\sum^m_{i=1}\bigg[-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))\bigg]+\frac{\lambda}{2m}\displaystyle\sum^n_{j=1}\theta^2_j J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
- 将 y = 1 y=1 y=1 和 y = 0 y=0 y=0 时的逻辑回归图像近似成两条直线组成的图像,从而带来计算上的优势,两个方程分别命名为 c o s t 1 ( z ) cost_1{(z)} cost1(z) 和 c o s t 0 ( z ) cost_0{(z)} cost0(z),下标表示 y = 1 y=1 y=1 和 y = 0 y=0 y=0 的情况。
- 忽略常数项 1 m \cfrac{1}{m} m1
- 考虑正则化项:逻辑回归: A + λ B A+\lambda B A+λB 支持向量机: C A + B CA+B CA+B
-
支持向量机:
-
代价函数: m i n θ C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) ) c o s t 0 ( θ T x ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 {min \atop \theta}C\displaystyle\sum^m_{i=1}\bigg[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)}))cost_0(\theta^Tx^{(i)})\bigg]+\cfrac{1}{2}\displaystyle\sum^n_{i=1}\theta^2_j θminCi=1∑m[y(i)cost1(θTx(i))+(1−y(i)))cost0(θTx(i))]+21i=1∑nθj2
-
假设函数:
h θ ( x ) = { 1 i f θ T x ≥ 0 0 o t h e r w i s e h_\theta(x)= \begin{cases} 1 & if \ \theta^Tx \geq 0 \\ 0 & otherwise \end{cases} hθ(x)={10if θTx≥0otherwise
-
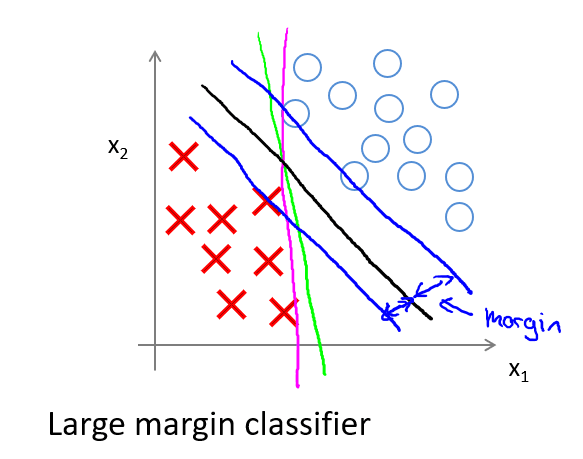
大间距的直观理解(Large Margin Intuition)
- 对支持向量机被称为大间距分类器的理解:
大间距分类背后的数学(The Mathematics Behind Large Margin Classification)
-
向量的内积等于投影和向量模的乘积:
u ⃗ × v ⃗ = u 1 v 1 + u 2 v 2 = u T v = v T u = p ⋅ ∥ u ∥ = p ⋅ ∥ v ∥ \vec {u} \times \vec {v} = u_1v_1 + u_2v_2 = u^Tv = v^Tu = p \cdot \begin{Vmatrix}u\end{Vmatrix} = p \cdot \begin{Vmatrix}v\end{Vmatrix} u×v=u1v1+u2v2=uTv=vTu=p⋅∥∥u∥∥=p⋅∥∥v∥∥
(第一个p是v在u上的投影,第二个p是u在v上的投影,p有正有负。)
-
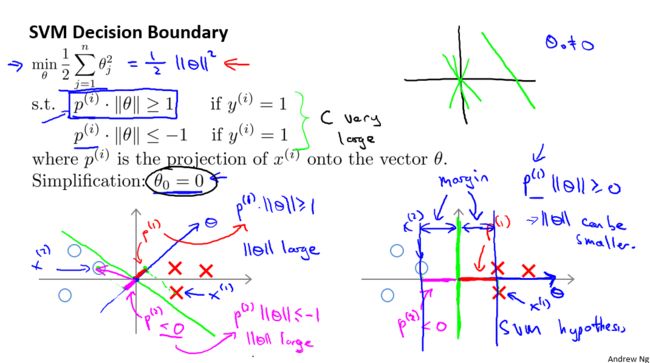
在SVM中:
m i n θ 1 2 ∑ j = 1 n θ j 2 min_\theta \cfrac{1}{2}\displaystyle\sum^n_{j=1}\theta^2_j minθ21j=1∑nθj2{ θ T x ( i ) ≥ 1 i f y ( i ) = 1 θ T x ( i ) ≤ − 1 i f y ( i ) = 0 \begin{cases} \theta^Tx^{(i)}\geq1 & if\ y^{(i)}=1\\ \theta^Tx^{(i)}\leq-1 & if\ y^{(i)}=0 \end{cases} {θTx(i)≥1θTx(i)≤−1if y(i)=1if y(i)=0
-
忽略截距 θ 0 = 0 \theta_0=0 θ0=0,假设特征数量 n = 2 n=2 n=2.
-
1 2 ∑ j = 1 n θ j 2 = 1 2 ( θ 1 2 + θ 2 2 ) = 1 2 ( θ 1 2 + θ 2 2 ) 2 = 1 2 ∥ θ ∥ 2 \cfrac{1}{2}\displaystyle\sum^n_{j=1}\theta^2_j=\cfrac{1}{2}(\theta^2_1+\theta^2_2)=\cfrac{1}{2}(\sqrt{\theta^2_1+\theta^2_2})^2=\cfrac{1}{2}\begin{Vmatrix}\theta\end{Vmatrix}^2 21j=1∑nθj2=21(θ12+θ22)=21(θ12+θ22)2=21∥∥θ∥∥2
-
θ T x ( i ) = p ∥ θ ∥ \theta^Tx^{(i)}=p\begin{Vmatrix}\theta\end{Vmatrix} θTx(i)=p∥∥θ∥∥
-
决策边界和 θ ⃗ \vec{\theta} θ是正交的
-
左图每个 x x x 向量在 θ \theta θ 上的投影距离都很小,要满足 p ( i ) ⋅ ∥ θ ∥ p^{(i)}\cdot\begin{Vmatrix}\theta\end{Vmatrix} p(i)⋅∥∥θ∥∥ 的条件则 ∥ θ ∥ \begin{Vmatrix}\theta\end{Vmatrix} ∥∥θ∥∥ 的值就要增大,但代价函数要求 ∥ θ ∥ \begin{Vmatrix}\theta\end{Vmatrix} ∥∥θ∥∥ 尽可能小,所以这不最优的。从而右图中的投影距离较大, ∥ θ ∥ \begin{Vmatrix}\theta\end{Vmatrix} ∥∥θ∥∥ 值较小,符合SVM中最小化目标函数的目的,即SVM是大间距分类器。
-
核函数1(Kernels Ⅰ)
-
目的: 对于一个非线性决策边界问题,我们可能使用高阶的函数进行拟合,是否存在比当前特征刚好的表达形式呢?(核函数)
-
为了获得图中的判定边界,我们的的模型可能为 θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 x 2 + θ 4 x 1 2 + θ 5 x 2 2 + ⋯ \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1x_2+\theta_4x^2_1+\theta_5x^2_2+\cdots θ0+θ1x1+θ2x2+θ3x1x2+θ4x12+θ5x22+⋯
可以将每种新的特征表示为 f i f_i fi,例如 f 1 = x 1 , f 2 = x 2 , f 3 = x 1 x 2 , f 4 = x 1 2 , f 5 = x 2 2 f_1=x_1, f_2=x_2,f_3=x_1x_2,f_4=x^2_1,f_5=x^2_2 f1=x1,f2=x2,f3=x1x2,f4=x12,f5=x22
则 h θ ( x ) = θ 1 f 1 + θ 2 f 2 + ⋯ + θ n f n h_\theta(x)=\theta_1f_1+\theta_2f_2+\cdots+\theta_nf_n hθ(x)=θ1f1+θ2f2+⋯+θnfn
-
除了对原有的特征进行组合以外,是否更好的方法来构造 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3?——我们可以利用核函数来计算出新的特征。
步骤:
-
随机选择三个点作为标记
-
地标(landmark)作用:
如果一个训练样本 x x x与地标 l l l之间的距离很近(相似度高),则 f f f近似于 e − 0 = 1 e^{-0}=1 e−0=1;
如果一个训练样本 x x x与地标 l l l之间的距离较远(相似度低),则 f f f近似于 e − ( 一 个 较 大 的 数 ) = 0 e^{-(一个较大的数)}=0 e−(一个较大的数)=0。
-
-
通过核函数得到 x x x对应的新特征
f 1 = s i m i l a r i t y ( x , l ( 1 ) ) = e x p ( − ∥ x − l ( 1 ) ∥ 2 2 σ 2 ) f_1=similarity(x,l^{(1)})=exp(-\cfrac{\begin{Vmatrix}x-l^{(1)}\end{Vmatrix}^2}{2\sigma^2}) f1=similarity(x,l(1))=exp(−2σ2∥∥x−l(1)∥∥2)
f 2 = s i m i l a r i t y ( x , l ( 2 ) ) = e x p ( − ∥ x − l ( 2 ) ∥ 2 2 σ 2 ) f_2=similarity(x,l^{(2)})=exp(-\cfrac{\begin{Vmatrix}x-l^{(2)}\end{Vmatrix}^2}{2\sigma }^{2}) f2=similarity(x,l(2))=exp(−2σ∥∥x−l(2)∥∥22)
f 3 = s i m i l a r i t y ( x , l ( 3 ) ) = e x p ( − ∥ x − l ( 3 ) ∥ 2 2 σ 2 ) f_3=similarity(x,l^{(3)})=exp(-\cfrac{\begin{Vmatrix}x-l^{(3)}\end{Vmatrix}^2}{2\sigma }^{2}) f3=similarity(x,l(3))=exp(−2σ∥∥x−l(3)∥∥22)
其中 ∥ x − l ( 1 ) ∥ = ∑ j = 1 n ( x j − l j ( 1 ) ) \begin{Vmatrix}x-l^{(1)}\end{Vmatrix}=\displaystyle\sum^n_{j=1}(x_j-l^{(1)}_j) ∥∥x−l(1)∥∥=j=1∑n(xj−lj(1)),为实例 x x x中所有特征与地标 l ( 1 ) l^{(1)} l(1)之间的距离的和。
当训练样本含两个特征时,给定地标 l ( 1 ) l^{(1)} l(1) 与不同的 σ \sigma σ 值,图像如下:
- 只有当 x x x与 l ( 1 ) l^{(1)} l(1)重合时 f f f才具有最大值。随着 x x x的改变 f f f值改变的速率受到 σ 2 \sigma^2 σ2的控制。
-
假设已经训练好参数 θ \theta θ,则可以通过 θ T f ≥ 0 \theta^Tf\geq0 θTf≥0来预测
-
当样本处于洋红色的点位置处,因为其离 l ( 1 ) l^{(1)} l(1)更近,但是离 l ( 2 ) l^{(2)} l(2)和 l ( 3 ) l^{(3)} l(3)较远,因此 f 1 f_1 f1接近1,而 f 2 f_2 f2, f 3 f_3 f3接近0。因此 h θ ( x ) = θ 0 + θ 1 f 1 + θ 2 f 2 + θ 1 f 3 > 0 h_θ(x)=θ_0+θ_1f_1+θ_2f_2+θ_1f_3>0 hθ(x)=θ0+θ1f1+θ2f2+θ1f3>0,因此预测 y = 1 y=1 y=1。
同理可以求出,对于离 l ( 2 ) l^{(2)} l(2)较近的绿色点,也预测 y = 1 y=1 y=1,但是对于蓝绿色的点,因为其离三个地标都较远,预测 y = 0 y=0 y=0。
-
这样,图中红色的封闭曲线所表示的范围,便是我们依据一个单一的训练样本和我们选取的地标所得出的判定边界,在预测时,我们采用的特征不是训练样本本身的特征,而是通过核函数计算出的新特征 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3。
-
核函数2(Kernels Ⅱ)
-
选择地标:
若训练集中有 m m m个样本则选择 m m m个地标,且 l ( 1 ) = x ( 1 ) , l ( 2 ) = x ( 2 ) , . . . . . , l ( m ) = x ( m ) l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},.....,l^{(m)}=x^{(m)} l(1)=x(1),l(2)=x(2),.....,l(m)=x(m)。
-
支持向量机:
- 假设函数: 给定 x x x,计算新特征 f f f,当 θ T f > = 0 θ^Tf>=0 θTf>=0 时,预测 y = 1 y=1 y=1,否则反之。
- 代价函数: m i n C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T f ( i ) ) + ( 1 − y ( i ) ) c o s t 0 ( θ T f ( i ) ) ] + 1 2 ∑ j = 1 n = m θ j 2 min \ C \displaystyle\sum^m_{i=1} \big[y^{(i)} cost_1 (\theta ^ T f ^ {(i)} ) + (1-y^{(i)}) cost_0 (\theta^T f^{(i)}) \big]+ \cfrac{1}{2} \displaystyle\sum^{n=m}_{j=1} \theta^2_j min Ci=1∑m[y(i)cost1(θTf(i))+(1−y(i))cost0(θTf(i))]+21j=1∑n=mθj2, ∑ j = 1 n = m θ j 2 = θ T θ \displaystyle\sum_{j=1}^{n=m} \theta_{j}^{2}=\theta^T \theta j=1∑n=mθj2=θTθ
-
在具体实施过程中,需要对正则化项进行调整,我们用时,我们用 θ T M θ θ^TMθ θTMθ代替 θ T θ θ^Tθ θTθ,其中 M M M是根据我们选择的核函数而不同的一个矩阵。这样做的原因是为了简化计算。理论上讲,我们也可以在逻辑回归中使用核函数,但是上面使用 M来简化计算的方法不适用与逻辑回归,因此计算将非常耗费时间。
另外,支持向量机也可以不使用核函数,不使用核函数又称为线性核函数(linear kernel),当我们不采用非常复杂的函数,或者我们的训练集特征非常多而样本非常少的时候,可以采用这种不带核函数的支持向量机。
-
两个参数 C C C 和 σ \sigma σ ( C = 1 λ C = \cfrac{1}{\lambda} C=λ1)
- C C C较大时,相当于 λ \lambda λ较小,可能会导致过拟合,高方差;
- C C C较小时,相当于 λ \lambda λ较大,可能会导致低拟合,高偏差;
- σ \sigma σ较大时,可能会导致低方差,高偏差;
- σ \sigma σ较小时,可能会导致低偏差,高方差。
使用支持向量机(Using An SVM)
-
核函数:
- 高斯核函数(Gaussian Kernel)
- 多项式核函数(Polynomial Kernel)
- 字符串核函数(String kernel)
- 卡方核函数( chi-square kernel)
- 直方图交集核函数(histogram intersection kernel)
-
多类分类问题:
- 可以训练 k k k个支持向量机来解决多类分类问题。
- 大多数支持向量机软件包都有内置的多类分类功能,我们只要直接使用即可。
-
模型选择: ( n n n 为特征数, m m m 为训练样本数)
- 如果相较于 m m m而言, n n n要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
- 如果 n n n较小,而且 m m m大小中等,例如 n n n在 1-1000 之间,而 m m m在10-10000之间,使用高斯核函数的支持向量机。
- 如果 n n n较小,而 m m m较大,例如 n n n在1-1000之间,而 m m m大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
神经网络在以上三种情况下都可能会有较好的表现,但是训练神经网络可能非常慢,选择支持向量机的原因主要在于它的代价函数是凸函数,不存在局部最小值。