python的第三方包Numpy简介(1)
一、关于Numpy
1.Numpy
Numpy是Python用于科学计算的基础包,也是大量Python数学和科学计算包的基础,不少数据处理及分析包都是在Numpy基础上开发的,比如后面介绍的pandas包就是在其基础上开发的。
Numpy的核心基础是ndarray(N-dimensional array,N维数组),即由数据类型相同的元素组成的N维数组。
2.利用
可利用Numpy包提供的数组定义函数array()将数据转化为数组的形式。
3.Numpy包的导入
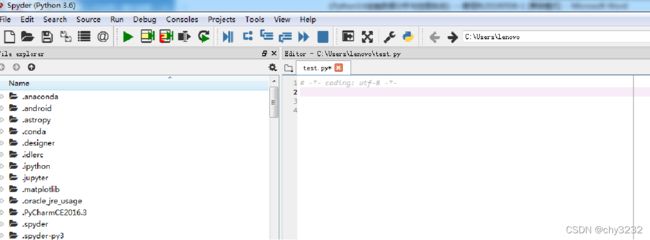
在Anaconda发行版中,Numpy包已集成在系统中,无需另外安装。那么如何使用该包呢?下面介绍如何在Python脚本文件中导入该包并使用。首先在打开的Spyder界面中新建一个脚本文件,如图2-1所示。
图2-1中新建了一个Python脚本文件,名称为test.py,并且处于编辑状态(文件名后面带“*”)。使用:import numpy命令,即可将该包导入到脚本文件中并可以使用了。
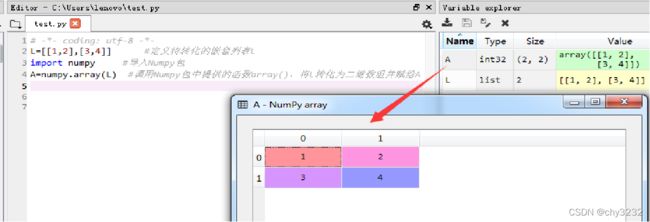
利用Numpy包提供的数组定义函数array(),将嵌套列表L=[[1,2],[3,4]]转化为二维数组。在test.py脚本文件中,输入以下示例代码: L=[[1,2],[3,4]] #定义待转化的嵌套列表L import numpy #导入Numpy包 A=numpy.array(L) #调用Numpy包中提供的函数array(),将L转化为二维数组并赋给A 执行test.py脚本文件,通过Spyder变量资源管理器双击变量A,即可查看其执行结果。如图2-2所示。
二、Numpy一些与数组相关的函数的使用方法
1.array()函数创建数组
基于array()函数,可以将列表、元组、嵌套列表、嵌套元组等给定的数据结构转化为数组,值得注意的是利用array函数之前,事先要导入Numpy
示例代码如下:
#1.先预定义列表d1,元组d2,嵌套列表d3、d4和嵌套元组d5
d1=[1,2,3,4,0.1,7] #列表
d2=(1,2,3,4,2.3) #元组
d3=[[1,2,3,4],[5,6,7,8]] #嵌套列表,元素为列表
d4=[(1,2,3,4),(5,6,7,8)] #嵌套列表,元素为元组
d5=((1,2,3,4),(5,6,7,8)) #嵌套元组
#2.导入Numpy,并调用其中的array函数,创建数组
import numpy as np
d11=np.array(d1)
d21=np.array(d2)
d31=np.array(d3)
d41=np.array(d4)
d51=np.array(d5)
#3. 删除d1,d2,d3,d4,d5变量
del d1,d2,d3,d4,d5
2.内置函数创建数组
利用内置函数,可以创建一些特殊的数组,比如可以利用ones(n,m)函数创建n行m列元素全为1的数组、利用zeros(n,m)函数创建n行m列元素全为0的数组,利用arange(a,b,c)创建以a为初始值,b-1为末值,c为步长的一维数组。其中a和c参数可省,这时a取默认值为0,c取默认值为1。
示例代码如下:
z1=np.ones((3,3)) #创建3行3列元素全为1的数组
z2=np.zeros((3,4)) #创建3行4列元素全为0的数组
z3=np.arange(10) #创建默认初始值为0,默认步长为1,末值为9的一维数组
z4= np.arange(2,10) #创建默认初始值为2,默认步长为1,末值为9的一维数组
z5= np.arange(2,10,2) #创建默认初始值为2,步长为2,末值为9的一维数组
3.数组的尺寸
数组尺寸,也称为数组的大小,通过行数和列数来表现。通过数组中的shape属性,可以返回数组的尺寸,其返回值为元组。如果是一维数组,返回的元组中仅一个元素,代表这个数组的长度。如果是二维数组,元组中有两个值,第一个值代表数组的行数,第二个值代表数组的列数。
示例代码如下:
d1=[1,2,3,4,0.1,7] #列表
d3=[[1,2,3,4],[5,6,7,8]] #嵌套列表,元素为列表
import numpy as np
d11=np.array(d1) #将d1列表转换为一维数组,结果赋值给变量d11
d31=np.array(d3) #将d3嵌套列表转换为二维数组,结果赋值给变量d31
del d1,d3 #删除d1,d3
s11=d11.shape #返回一维数组d11的尺寸,结果赋值给变量s11
s31=d31.shape #返回二维数组d31的尺寸,结果赋值给变量s314.数组重排——reshape()
在程序应用过程中,有时候需要将数组进行重排,可以通过reshape()函数来实现。
示例代码如下:
r=np.array(range(9)) #一维数组 r1=r.reshape((3,3)) #重排为3行3列5.数组的运算——加、减、点乘、乘、除、乘方
数组的运算主要包括数组之间的加、减、乘、除运算,数组的乘方运算,以及数组的数学函数运算。
示例代码如下:
import numpy as np
A=np.array([[1,2],[3,4]]) #定义二维数组A
B=np.array([[5,6],[7,8]]) #定义二维数组B
C1=A-B #A、B两个数组元素之间相减,结果赋给变量C1
C2=A+B #A、B两个数组元素之间相加,结果赋给变量C2
C3=A*B #A、B两个数组元素之间相乘,结果赋给变量C3
C4=A/B #A、B两个数组元素之间相除,结果赋给变量C4
C5=A/3 #A数组所有元素除以3,结果赋给变量C5
C6=1/A #1除以A数组所有元素,结果赋给变量C6
C7=A**2 # A数组所有元素取平方,结果赋给变量C7
C8=np.array([1,2,3,3.1,4.5,6,7,8,9]) #定义数组C8
C9=(C8-min(C8))/(max(C8)-min(C8)) #C8中的元素做极差化处理,结果赋给变量C9
D=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]]) #定义数组D
#数学运算
E1=np.sqrt(D) #数组D中所有元素取平方根,结果赋给变量E1
E2=np.abs([1,-2,-100]) #取绝对值
E3=np.cos([1,2,3]) #取cos值
E4=np.sin(D) #取sin值
E5=np.exp(D) #取指数函数值
6.数组的切片
一般地,假设D为待访问或切片的数据变量,则访问或者切片的数据=D[①,②]。其中①为对D的行下标控制,②为对D的列下标控制,行和列下标控制通过整数列表来实现,但是需要注意①整数列表中的元素不能超出D中的最大行数,而②不能超过D中的最大列数。为了更灵活地操作数据,取所有的行或者列,可以用“:”来代替实现。同时,行控制还可以通过逻辑列表来实现。
示例代码如下:
import numpy as np
D=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]]) #定义数组D
#访问D中行为1,列为2的数据,注意下标是从0开始的。
D12=D[1,2]
#访问D中第1、3列数据
D1=D[:,[1,3]]
# 访问D中第1、3行数据
D2=D[[1,3],:]
# 取D中满足第0列大于5的所有列数据,本质上行控制为逻辑列表
Dt1=D[D[:,0]>5,:]
#取D中满足第0列大于5的2、3列数据,本质上行控制为逻辑列表
#Dt2=D[D[:,0]>5,[2,3]]
TF=[True,False,False,True]
#取D中第0、3行的所有列数据,本质上行控制为逻辑列表,取逻辑值为真的行
Dt3=D[TF,:]
#取D中第0、3行的2、3列数据
#Dt4=D[TF,[2,3]]
# 取D中大于4的所有元素
D5=D[D>4]
数组的切片,也可以通过ix_()函数构造行、列下标索引器,实现数组的切片操作
代码如下:
import numpy as np
D=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]]) #定义数组D
#提取D中行数为1、2,列数为1、3的所有元素
D3=D[np.ix_([1,2],[1,3])]
#提取D中行数为0、1,列数为1、3的所有元素,其中行数
D4=D[np.ix_(np.arange(2),[1,3])]
#提前以D中第1列小于11得到的逻辑数组作为行索引,列数为1、2的所有元素
D6=D[np.ix_(D[:,1]<11,[1,2])]
#提前以D中第1列小于11得到的逻辑数组作为行索引,列数为2的所有元素
D7=D[np.ix_(D[:,1]<11,[2])]
#提前以2.5.1中的TF=[True,False,False,True]逻辑列表为行索引,列数为2的所有元素
TF=[True,False,False,True]
D8=D[np.ix_(TF,[2])]
#提前以2.5.1中的TF=[True,False,False,True]逻辑列表为行索引,列数为1,,3的所有元素
D9=D[np.ix_(TF,[1,3])]
7.数组的链接
在数据处理中,多个数据源的集成整合是经常发生的。对于数组间的集成与整合,主要体现在数组间的连接,包括水平连接和垂直连接两种方式。水平连接函数用hstack()、垂直连接函数用vstack()实现。注意输入参数为两个待连接数组组成的元组。
示例代码如下:
import numpy as np
A=np.array([[1,2],[3,4]]) #定义二维数组A
B=np.array([[5,6],[7,8]]) #定义二维数组B
C_s=np.hstack((A,B)) #水平连接要求行数相同
C_v=np.vstack((A,B)) #垂直连接要求列数相同
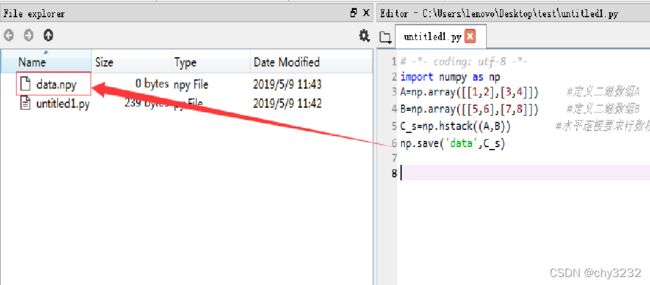
8.数组的存取——save函数、load函数
利用Numpy库中的save函数,可以将数据集保存为二进制数据文件,数据文件后缀名为.npy。
示例代码如下:
import numpy as np
A=np.array([[1,2],[3,4]]) #定义二维数组A
B=np.array([[5,6],[7,8]]) #定义二维数组B
C_s=np.hstack((A,B)) #水平连接
np.save('data',C_s)
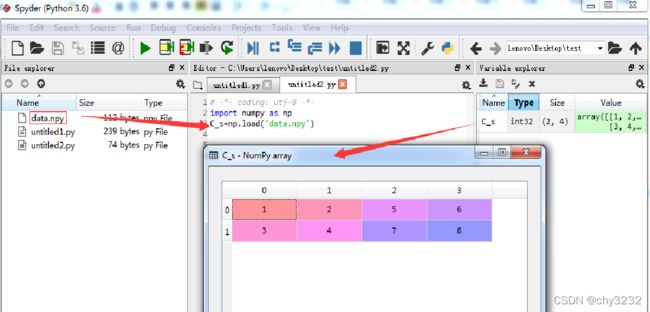
通过load函数,可以将该数据集加载
例代码如下:
import numpy as np
C_s=np.load(‘data.npy’)其显示了将data.npy这个数据文件加载下来,并通过Spyder变量资源管理器查看其结果的过程。通过数据的存取机制,提供了数据传递及使用的便利,特别是有些程序运行结果需要花费大量时间的时候,保存其结果以便后续使用是非常有必要的。