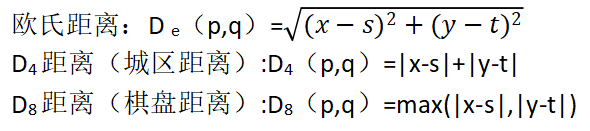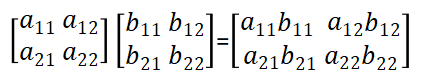数字图像处理知识点梳理——第二章 数字图像基础

2.1 视觉感知要素

（1） 人的视觉系统构成：眼球、神经系统、大脑的视觉中枢

（2）两类光感受器：锥状体（Cones）和杆状体（rods）：

锥状体视觉称为白昼视觉或亮视觉，对颜色十分敏感；
杆状体视觉称为暗视觉或微光视觉。

在低照明水平情况下，视觉由杆状体执行，在高照明水平情况下，视觉由锥状体执行。

（3）人的视觉过程：光刺激->视网膜接收->视网膜神经处理->视觉通道->大脑皮层处理->响应

（4）主观亮度是眼睛入射光强的对数函数，亮度适用范围是从10^-6到10⁴，视觉系统通过改变其整个灵敏度来完成这一较大的变动，这就是亮度适应现象；视觉系统的当前灵敏度级别称为亮度适应级别。

（5）用于确定人类视觉系统亮度辨别能力的一个著名实验：光强为I，照射分量为ΔI，ΔI_c/I称为韦伯比（其中ΔI_c是在背景照明为I时可辩别照明增量的50%）。韦伯比较小意味着可辩别强度较小的百分比变化，表示亮度辨别能力强，反之，意味着要求有较大百分比的强度变化，表示亮度辨别能力差。

2.2 光和电磁波谱

总结：

• 电子伏特越大，电磁波谱频率越小、波长越大，则在可见光谱中，越接近红色。
• 没有颜色的光称为单色光或无色光，从黑到白的单色光的度量值范围通常称为 灰度级，而单色图像常称为 灰度图像。

2.3 图像感知和获取

总结：

• 可使用单个传感器获取图像；
• 可使用条带传感器获取图像；
• 可使用传感器阵列获取图像；

简单的图像形成模型：f(x,y)=i(x,y)r(x,y)，其中i(x,y)的性质取决于照射源，r(x,y)的性质取决于成像物体的特性。

图像获取即图像的数字化过程，包括扫描、取样和量化。

2.4 图像取样和量化

2.4.1 取样和量化的基本概念

图像的取样：将空间上连续的图像变换成离散点，对坐标值进行数字化的操作，相当于对位置离散；
图像的量化：将像素灰度转换成离散的整数值，即对幅值数字化的过程，相当于对亮度离散。

数字图像的质量在很大程度上取决于取样和量化中所用的样本数和灰度级:

• 一般来说，取样间隔越大，所得图像像素数越少，空间分辨率越低，质量越差，严重时出现马赛克效应
• 量化等级越多，所得图像层次越丰富，灰度分辨率越高，图像质量越好，但数据量大。

2.4.2 数字图像表示

数字图像的原点位于左上角，其中正x轴向下延伸，正y轴向右延伸，假设把连续图像取样为一个二维阵列f(x,y)，该阵列包含有M行和N列，其中(x,y)是离散坐标，设离散灰度级数为L（L=2^k），则存储数字图像所需的比特数b为b=M×N×k，M=N时，b=N×2^k。

2.4.3 空间和灰度分辨率

• 空间分辨率是图像中可辩别的最小细节的度量；
• 灰度分辨率是指在灰度级中可分辨的最小变化。

2.4.4 图像内插

内插属于基本的图像重取样方法，在放大、收缩、旋转和几何校正中有广泛的应用。第四章会重点介绍。目前可简单了解到，插值有最近邻内插、双线性内插和双三次内插。其操作越来越复杂，效果也越来越好。

2.5 像素间的一些基本关系

2.5.1 相邻像素

位于坐标(x,y)处的像素p的4个水平和垂直的相邻像素，这组像素称为p的4邻域，记为 N₄( p)；
位于坐标(x,y)处的像素p的4个对角相邻像素，记为N_D( p);
N₄( p)∪ N_D( p); = N₈( p)。

2.5.2 邻接性、连通性、区域和边界

• 邻接性
  4邻接
  8邻接
  m邻接
  (设V={1})

• 连通性

设S是像素集，p、q∈S，如果在S中存在一条从p到q的通路，那么称p和q在S中是连通的。对于S中的任何像素p，S中连通到该像素集称为S的连通分量，如果S只有一个连通分量，则集合S称为连通集。

• 区域

设R₁,R₂是区域，如果R₁∪R₂是连通的，称R₁,R₂相邻，不邻接的区域称为不连接区域。

• 边界

区域R中与其补集R^c相邻的像素集合称为区域R的边界，也成为内边界；
补集R^c中与R相邻的像素集合，称为区域R的外边界

2.5.3 距离度量

2.6 数字图像处理中所用数学工具的介绍

2.6.1 阵列与矩阵操作

区别阵列与矩阵操作，我们假设阵列操作贯穿全书，除非另作说明。

阵列相乘:

2.6.2 图像运算总结

（1）点运算：

对每个像素点的像素值进行变换，包括线性变换和非线性变换。

• 线性变换：输入图像的灰度级与输出图像的灰度级呈线性关系，即s=ar+b(r为输入图像点的灰度值，s为相应输出点的灰度值)
  线性变化运行结果图

• 典型的非线性变换函数有：对数函数、指数函数、幂函数、阈值函数、多值量化函数、窗口函数等。

I=imread('eight.tif');                            %读取一幅图片
I = im2double(I);                                 % 转类型为double
subplot(1,5,1);
imshow(I);                                        % 显示原图像
title('原图像','fontsize',6);    
a = 2; b = -50;                                   % a>1,增加对比度
O = a .* I + b/255;
subplot(1,5,2);
imshow(O);
title('a=2,b=-50,增加对比度','fontsize',6);
a = 0.5; b = -50;                                 % a<1,减小对比度
O = a .* I + b/255;
subplot(1,5,3); 
imshow(O);
title('a=0.5,b=-50,减小对比度','fontsize',6);
a = 1; b = 50;                                    % a=1,线性改变亮度  
O = a .* I + b/255;
subplot(1,5,4);
imshow(O);
title('a=1,b=50,改变亮度','fontsize',6);
a = -1; b = 300;                                  % a<0, 图像求补  
O = a .* I + b/255;
subplot(1,5,5);
imshow(O);
title('a=-1,b=300,图像求补','fontsize',6);

（2）代数运算：

对二幅或多幅图像像素值进行加、减、乘、除。

加法降噪，减法检测变化，乘法用来屏蔽图像的某些部分，除法校正明暗变化
加法运行结果图
减法运行结果图
乘法运行结果图
除法运行结果图

（3）逻辑运算：

对二幅二值图像像素进行逻辑与、或、非、异或。

逻辑 与 或 非 异或 运行结果图

（4）几何运算：

不改变像素值，而改变像素所在的位置，如平移、镜像、旋转、缩小、放大等。

一个几何运算需要两个独立的算法：
一个算法来定义空间变换；一个算法用于灰度级的插值

• 放缩：一般是全比例缩放，如果x方向和y方向缩放比例不同，则图像的比例缩放会改变原始图像像素间的相对位置，产生几何畸变。
• 旋转（以图像的中心为原点）：

旋转变换后，图像位置发生变化，解决方法：

• 截去区域外的部分
• 扩大显示区域的图像范围以显示图像的全部

图像旋转后，可能会出现一些空白点，需要对这些空白点进行灰度级的插值处理,插值方法见2.4.4

关键代码如下：

• 平移：J = imtranslate(I,[200,100]);平移运行结果图

• 放缩：J = imresize(I,0.5);放缩运行结果图

• 旋转：J = imrotate(I,30);旋转运行结果图

• 镜像：
  M = [-1,0,0;0,1,0;0,0,1];
  t = affine2d(M);
  J = imwarp(I,t);
  镜像运行结果图