【论文解读】CIKM 2022: STID: A Simple yet Effective Baseline for Multivariate Time Series Forecasting

同时对多个区域进行序列预测，会在我们工作生活中经常预测：

• 多个城市每日销售量预测
• 多个渠道每日需求量预测
• 不同景点人流量预测等

一、摘要

STGNNs在多维序列预测中表现超前，所以近期的多数研究都是基于此进行。而本文提出了基于序列、时间、空间编码，的简单Spatial and Temporal IDentity (STID)模型结构。其效果在多维序列预测任务上运行速度快，同时效果好，效果比邻甚至超越STGNNs。

二、简介

论文的背景知识，前人的工作等

多序列预测往往之间具有一定的相关性。
前人工作主要两大方向：

• GCN + RNN:
  • 2018-ICLR，MTS预测领域最经典的Baseline之一 DCRNN：
    • 将交通系统的每个时刻，建模为车辆沿着路网的扩散过程（Diffusion Process）。具体的方法是：将自己设计的GCN的变体，替换掉GRU内部的全连接层，从而使得GRU可以处理MTS数据。它是把GRU打破了，将其内部的全连接进行替换，而非简单堆叠GCN和GRU。
  • 这思路可以追溯到NeurIPS 2015上的一篇论文convLSTM：将CNN替换掉LSTM中的全连接层。
• GCN + CNN:
  • 2019- IJCAI，另一个经典的Baseline：Graph WaveNet。
    • 它将GCN和TCN（一种处理时间序列的卷积网络）有机的结合到一起。

本文作者突破STGNNs的限制设计一个不一样简单且同样有效的网络。

三、Model Architecture

• Embedding 层:
  • 空间信息: $\mathbf{E}\in {\mathbf{R}}^{\mathbf{N}\times \mathbf{D}}$
    • One-hot 空间$\mathbf{N}$ ：不同空间的总数(地区、城市等)
  • 时间信息（time in day）： ${\mathbf{T}}^{\mathbf{T}\mathbf{i}\mathbf{D}}\in {\mathbf{R}}^{{\mathbf{N}}_{\mathbf{d}}\times \mathbf{D}}$
    • One-hot 空间${\mathbf{N}}_{\mathbf{d}}=288$: 5分钟一个时间片
  • 时间信息（day in week）： ${\mathbf{T}}^{\mathbf{D}\mathbf{i}\mathbf{W}}\in {\mathbf{R}}^{{\mathbf{N}}_{\mathbf{w}}\times \mathbf{D}}$
    • One-hot 空间${\mathbf{N}}_{\mathbf{w}}=7$: 7天一周
  • 时间序列（时序做全连接层输出）：这部分Github实现和论文有点不一样
    • 论文：$H_t^i=FC(X_{his}^i)$
    • 实现：将 [time_sires, time_in_day, day_in_week] 连接起来放入全连接层

        # ts embedding
        batch_size, _, num_nodes, _ = input_data.shape
        # (batch_size, samples, num_nodes, channel) -> (batch_size, num_nodes, samples, channel)
        input_data = input_data.transpose(1, 2).contiguous()
        # 转成 data - time-in-day - day-of-week 的序列
        # (batch_size, num_nodes, samples, channel) -> (batch_size, num_nodes, samples * channel) 
        #    -> (batch_size, samples * channel, num_nodes) -> (batch_size, samples * channel, num_nodes, 1)
        input_data = input_data.view(batch_size, num_nodes, -1).transpose(1, 2).unsqueeze(-1)
        
        # (batch_size, samples * channel, num_nodes, 1) -> (batch_size, embed_dim, num_nodes, 1) 
        time_series_emb = self.time_sires_emb_layer(input_data)

• Embedding Concat:
  • $Z_i=H_t^i||E_i||T_i^{TiD}||T_i^{DiW}$
• 多层全连接层（l-th MLP）:
  • $(Z^i{)}^{l+1}=F{C}_2^l(\sigma (F{C}_1^l((Z_t^i{)}^l)+(Z_t^i{)}^l$
• 回归输出层
  • $Y=F{C}_{regression}(Z)$

四、研究成果及效果讨论

在5个数据集上得到了最优 结果

Embedding学习到的物理特征

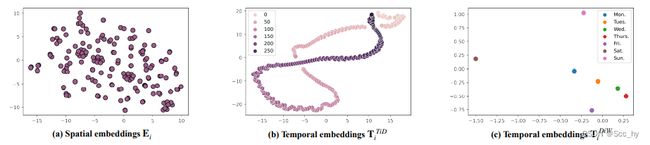
• Spatial embedding ： 具有聚类作用
• Temporal embedding Tid： 具有周期性
• Temporal embedding Diw： 区分工作日与周末：工作日相似，周末不一样

五、论文总结

关键点

提出序列预测的STID模型架构

• 不同于两种主力方向
  • GCN + RNN： DCRNN
  • GCN + TCN： Graph WaveNet
• 训练速度更快、效果更好

创新点

重新审视一下MTS预测这个问题，重新思考一下它和普通的时间序列预测问题的不同之处到底在哪里，而不应该将自己的局限在时空图神经网络中。
设计了一个简单有效的STID模型架构

启发点

从任务的核心点出发设计更加简单的模型结构

六、PEMS-BAY数据集复现STID

源码比较让笔者难受的是全连接用的都是nn.Conv2d。
笔者做了一些改动。最终模型如下：
全部的复现代码可以看笔者在kaggle的复现STID-recurrence

class MyMultiLayerPerceptron(nn.Module):
    def __init__(self, input_dim, hidden_dim):
        super(MyMultiLayerPerceptron, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim, bias=True)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim, bias=True)
        self.act = nn.ReLU()
        self.drop = nn.Dropout(p=0.15)
    
    def forward(self, in_data):
        # in_data: [B, D, N]
        out = self.act(self.fc1(in_data))
        out = self.fc2(self.drop(out))
        return out + in_data


class MYSTID(nn.Module):
    def __init__(self, model_kwargs):
        super(MYSTID, self).__init__()
        # attributes
        self.num_nodes = model_kwargs['num_nodes']
        self.node_dim = model_kwargs['node_dim']
        self.input_len = model_kwargs['input_len']
        self.input_dim = model_kwargs['input_dim']
        self.embed_dim = model_kwargs['embed_dim']
        self.output_len = model_kwargs['output_len']
        self.num_layer = model_kwargs['num_layer']
        self.temp_dim_tid = model_kwargs['temp_dim_tid']
        self.temp_dim_diw = model_kwargs['temp_dim_diw']
        
        self.if_time_in_day = model_kwargs['if_T_i_D']
        self.if_day_in_week = model_kwargs['if_D_i_W']
        self.if_spatial = model_kwargs['if_node']
        self.device = model_kwargs['device']
        
        # # spatial embeddings (nn.init.xavier_uniform_(self.node_emb))
        self.node_emb = nn.Embedding(num_embeddings=self.num_nodes, embedding_dim=self.node_dim)
        # temporal embeddings
        self.time_in_day_emb = nn.Embedding(num_embeddings=288, embedding_dim=self.temp_dim_tid)
        self.day_in_week_emb = nn.Embedding(num_embeddings=7, embedding_dim=self.temp_dim_diw)
        # embedding layer
        self.time_sires_emb_layer = nn.Linear(in_features=self.input_dim * self.input_len, out_features=self.embed_dim, bias=True)
        # encoding
        self.hidden_dim = self.embed_dim + self.node_dim * int(self.if_spatial) + \
                            self.temp_dim_tid * int(self.if_time_in_day) + \
                            self.temp_dim_diw * int(self.if_day_in_week)
        self.encoder = nn.Sequential(
            *[MyMultiLayerPerceptron(self.hidden_dim, self.hidden_dim) for _ in range(self.num_layer)]
        )
        
        # regression
        self.regression_layer = nn.Linear(self.hidden_dim, self.output_len, bias=True)

    def forward(self, his_data):
        """Feed forward of STID.
        Args:
            his_data (torch.Tensor): history data with shape [B, L, N, C]
        Returns:
            torch.Tensor: prediction wit shape [B, L, N, C]
        """
        # prepare
        input_data = his_data[..., range(self.input_dim)]
        time_in_day_emb = None
        if self.if_time_in_day:
            t_i_d_data = (his_data[:, -1, :, 1] * 288).type(torch.LongTensor).to(self.device)
            # (b, node_nums(time_in_day dim-len)) -> T^{TiD}(Nd x D)-> (b, node_nums(time_in_day dim-len), emb)
            time_in_day_emb = self.time_in_day_emb(t_i_d_data)
    
        day_in_week_emb = None
        if self.if_day_in_week:
            d_i_w_data = (his_data[:, -1, :, 2]).type(torch.LongTensor).to(self.device)
            # (b, node_nums(day_in_week dim-len)) -> T^{DiW}(Nw x D)-> (b, node_nums(day_in_week dim-len), emb)
            day_in_week_emb = self.day_in_week_emb(d_i_w_data)

        # ts embedding
        batch_size, _, num_nodes, _ = input_data.shape
        # (b, L, num_nodes, channel) -> (b, num_nodes, L, channel) ->
        # (b, num_nodes, L, channel) -> (b, num_nodes, L * channel) (data || time-in-day || day-of-week)
        input_data = input_data.transpose(1, 2).contiguous()
        input_data = input_data.view(batch_size, num_nodes, -1)
        # (b, num_nodes, L * channel) -> FC_emb (L*channel, D) -> (b, num_nodes, emb) 
        time_series_emb = self.time_sires_emb_layer(input_data)

        # node emb
        # (b, node_nums)
        nodes_indx = torch.Tensor([list(range(num_nodes)) for _ in range(batch_size)]).long().to(self.device)
        node_emb = []
        if self.if_spatial:
            node_emb.append(
                # (b, node_nums) -> E(N x D) -> (b, node_nums, emb)
                self.node_emb(nodes_indx)
            )

        # time embedding
        tem_emb = []
        if self.if_time_in_day:
            tem_emb.append( time_in_day_emb )
        if self.if_day_in_week:
            tem_emb.append( day_in_week_emb )
        
        # concat (b, num_node, 32*4)
        hidden = torch.cat([time_series_emb] + node_emb + tem_emb, dim=2)
        # (b, num_node, 32*4) -> (b, num_node, 32*4)
        hidden = self.encoder(hidden)
        # (b, num_node, 32*4) -> (b, num_node, out_len)
        pred = self.regression_layer(hidden)
        # print('pred - pred.shape:', pred.shape)
        return pred.transpose(1, 2).contiguous()