数据结构与算法之美笔记(三)排序

排序

如何分析一个“排序算法”？

1. 排序算法的执行效率
   1.1 最好情况、最坏情况、平均情况时间复杂度
   1.2 时间复杂度的系数、常数 、低阶
   1.3 比较次数和交换（或移动）次数
2. 排序算法的内存消耗
3. 排序算法的稳定性

为什么要考察排序算法的稳定性呢？
答：在真正软件开发中，我们要排序的往往不是单纯的整数，而是一组对象，我们需要按照对象的某个key来排序。比如有下单时间和商品价格两个属性，对价格排序后还需要在相同价格内保证下单时间有序的话，就需要稳定排序算法了。

---

冒泡排序

冒泡排序代码
isOrderly用于在发现数组已经有序时进行提前结束排序

static void bubbleSort(int[] arr){
        int len=arr.length;
        for(int i=0;i<len;i++){
            boolean isOrderly=true;
            for(int j=0;j<len-i-1;j++){
                if(arr[j]>arr[j+1]){
                    isOrderly=false;
                    int tmp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=tmp;
                }
            }
            if(isOrderly){ break; }
        }
    }

算法分析：
1、空间复杂度：只有交换操作和几个临时变量 即O(1)
2、稳定性：代码中相邻两数相等时不会进行交换，维护了稳定性
3、时间复杂度：
最好情况O(n) （至少也要一次遍历）
最坏情况O(n^2) （纯粹的倒序）

作者这里讲了一种分析平均时间复杂度的方法：使用逆序数和有序数
逆序对：a[i] >= a[j] 且 i < j，则这里称为一个逆序对
逆序数：数组中逆序对的个数，有序对同理
我们还可以得到一个公式：逆序度=满有序度-有序度。我们排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，

---

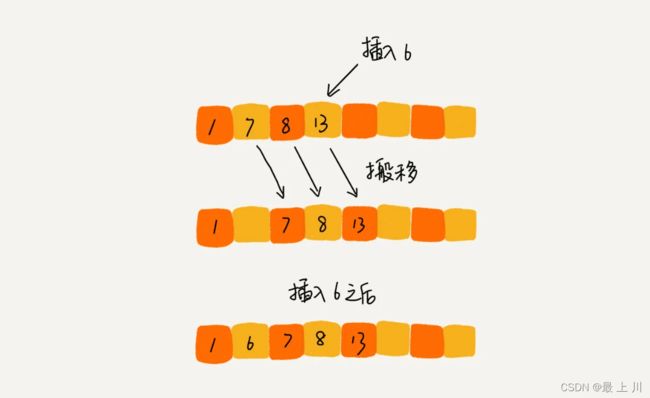
插入排序

思想：将数组中的数据分为两个区间，已排序区间和未排序区间，取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。

static void insertionSort(int[] arr){
        int len=arr.length;
        for(int i=1;i<len;i++){
            int temp=arr[i];
            int j=i-1;
            for(;j>=0;j--){
                if(arr[j]<=temp){
                    break;
                }
                arr[j+1]=arr[j];
            }
            //注意这里必须写在外面，不能写在break前一句
            arr[j+1]=temp;
        }
    }

算法分析：
1、空间复杂度：O(1)
2、稳定性：对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。
3、时间复杂度：最好O(n)，最坏和平均O(n^2)

---

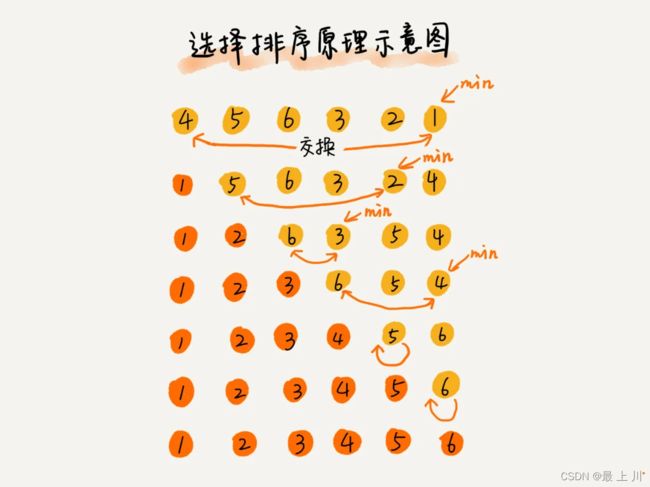
选择排序
也是把数组分为有序和无序的两部分，但是每次是从无序中选取最值，放在有序部分的尾部，但是因为这个“放在”其实是交换操作，使得选择排序不具有稳定性

static void selectionSort(int[] arr){
  	int len=arr.length;
    for(int i=0;i<len-1;i++){
        int min=Integer.MAX_VALUE;
        int tag=i;
        //得到无序部分最小值
        for(int j=i;j<len;j++){
            if(min>arr[j]){
                min=arr[j];
                tag=j;
            }
        }
        if(tag!=i){
            int temp=arr[tag];
            arr[tag]=arr[i];
            arr[i]=temp;
        }
    }
}

算法分析：
1、空间复杂度：O(1)
2、稳定性：不稳定
3、时间复杂度：最好O(n)，最坏和平均O(n^2)

---

这里作者还说了一下

我们把执行一个赋值语句的时间粗略地计为单位时间（unit_time），然后分别用冒泡排序和插入排序对同一个逆序度是K的数组进行排序。用冒泡排序，需要K次交换操作，每次需要3个赋值语句，所以交换操作总耗时就是3*K单位时间。而插入排序中数据移动操作只需要K个单位时间。
这个只是我们非常理论的分析，为了实验，针对上面的冒泡排序和插入排序的Java代码，我写了一个性能对比测试程序，随机生成10000个数组，每个数组中包含200个数据，然后在我的机器上分别用冒泡和插入排序算法来排序，冒泡排序算法大约700ms才能执行完成，而插入排序只需要100ms左右就能搞定！
所以，虽然冒泡排序和插入排序在时间复杂度上是一样的，都是O(n2)，但是如果我们希望把性能优化做到极致，那肯定首选插入排序。

---

然后翻出来我以前写的希尔排序（算是插入排序的优化吧）
空间复杂度O(1)，平均时间复杂度O(nlogn)
由于记录跳跃式的移动，希尔排序并不是一种稳定的排序方法。

下面是我从别人博客那复制过来的演示动图
可以很清晰的理解 “增量”的概念

void ShellSort(int N,int *a)
{
	int gap,temp;
	int i,j;
	for(gap=N/2;gap>0;gap/=2)
	{
		for(i=gap+1;i<=N;i++)
		{
			temp=a[i];
			for(j=i-gap;j>=0&&a[j]>temp;j-=gap)
			{
				a[j+gap]=a[j];
			}
			a[j+gap]=temp;
		}
	}
}

---

归并排序
先分解问题，再由处理好的子问题结果得到当前结果
即分治思想
这里对于两个有序的子数组合并得到当前的有序数组，用到了临时数组，使空间复杂度来到了O(n)

以前写的归并排序

void Merge(int *a,int left,int mid,int right)
{
	int temp[10000];//数组大小至少等于题给数组的大小
	//temp数组作为临时数组，存放区间在left~right的有序数组元素，
	//再赋值给原数组，起到排序的作用 
	int i,j,k;
	
	i=left,j=mid+1,k=1;//temp数组下标也从1开始 
	//左边数组从1~mid，右边从mid+1~right 
	//必须要这样，和Mergesort里的参数要一致，否则会出错 
	while(i<=mid&&j<=right)
	{
		if(a[i]<a[j])
		{
			temp[k++]=a[i++];
		}
		else
		{
			temp[k++]=a[j++];
		}
	}
	if(i<=mid)
	{
		while(i<=mid)
		{
			temp[k++]=a[i++];
		}
	}
	if(j<=right)
	{
		while(j<=right)
		{
			temp[k++]=a[j++];
		}
	}
	for(i=left,k=1;i<=right;i++,k++)
	{//把有序的子数组放入a数组中
		a[i]=temp[k];//非常要注意各种变量的正确位置 
	}
}
//主函数调用的是Mergesort函数
void MergeSort(int *a,int left,int right)
{
	if(left>=right)
	{
		return;
	}
	int mid=left+(right-left)/2;
	//分 
	MergeSort(a,left,mid);
	MergeSort(a,mid+1,right);
	//并 
	Merge(a,left,mid,right);
}

算法分析：
1、空间复杂度：临时数组 O(n)
2、稳定性：当规定遇到相同数字时先往临时数组里放左边数组的元素时，具有稳定性
3、时间复杂度：最好O(n)，最坏和平均O(n^2)

学习一下作者求这种递归算法时间复杂度的思路

我们假设对n个元素进行归并排序需要的时间是T(n)，那分解成两个子数组排序的时间都是T(n/2)。我们知道，merge()函数合并两个有序子数组的时间复杂度是O(n)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是：

T(1) = C； n=1时，只需要常量级的执行时间，所以表示为C。
T(n) = 2T(n/2) + n； n>1
通过这个公式，如何来求解T(n)呢？还不够直观？那我们再进一步分解一下计算过程。
T(n) = 2T(n/2) + n
= 2*(2T(n/4) + n/2) + n = 4T(n/4) + 2n
= 4(2T(n/8) + n/4) + 2n = 8T(n/8) + 3n
= 8*(2T(n/16) + n/8) + 3n = 16T(n/16) + 4n
…
= 2^k * T(n/2^k) + k * n
…

通过这样一步一步分解推导，我们可以得到T(n) = 2^kT(n/2k)+kn。当T(n/2^{k)=T(1)时，也就是n/2}k=1，我们得到k=log2n 。我们将k值代入上面的公式，得到T(n)=Cn+nlog2n 。如果我们用大O标记法来表示的话，T(n)就等于O(nlogn)。所以归并排序的时间复杂度是O(nlogn)。

从我们的原理分析和伪代码可以看出，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是O(nlogn)。

作者说的一个对于归并排序空间复杂度判断的误区：
logn的深度，每层都有临时数组。所以空间复杂度为O(nlogn),对吗？
答：错，因为尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。

---

快速排序
这个太熟了就不怎么写了

---

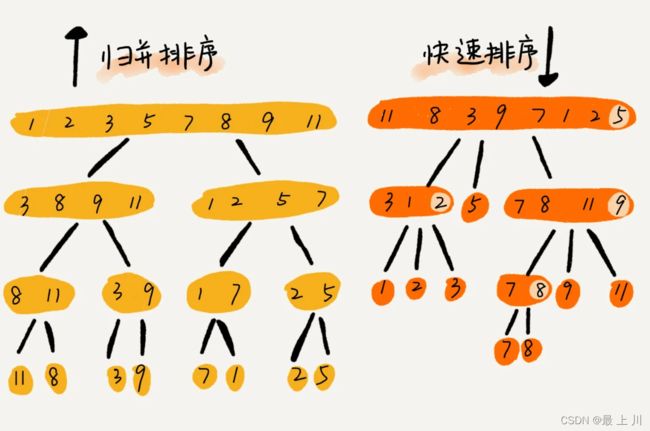
可以发现，归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为O(nlogn)的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。但是也要注意，快排的执行效率与要排序的原始数组的有序程度存在关联，如果数组完全倒序，则每次只将数组划分为长度分为n-1和0的数组，即最坏时间复杂度来到了O(n^2)，但是快速排序算法时间复杂度退化到O(n2)的概率非常小，我们可以通过合理地选择pivot来避免这种情况。

---

线性排序

时间复杂度是O(n)的排序算法：桶排序、计数排序、基数排序

---

桶排序
核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

---

计数排序
计数排序只能用在数据范围不大的场景中，如果数据范围k比要排序的数据n大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。
下文参考自基数排序、桶排序和计数排序的区别

其思路是开一个长度为 maxValue-minValue+1 的数组，然后 分配。扫描一遍原始数组，以当前值- minValue
作为下标，将该下标的计数器增1。 收集。扫描一遍计数器数组，按顺序把值收集起来。 举个例子， nums=[2, 1, 3, 1, 5] ,
首先扫描一遍获取最小值和最大值， maxValue=5 , minValue=1 ，于是开一个长度为5的计数器数组 counter ，

1. 分配。统计每个元素出现的频率，得到 counter=[2, 1, 1, 0, 1] ，例如 counter[0] 表示值 0+minValue=1 出现了2次。
2. 收集。 counter[0]=2 表示 1 出现了两次，那就向原始数组写入两个1，
3. counter[1]=1 表示 2 出现了1次，那就向原始数组写入一个2，依次类推，最终原始数组变为 [1,1,2,3,5] ，排序好了。

---

基数排序
下文也参考自基数排序、桶排序和计数排序的区别
它的主要思路是，

1. 将所有待排序整数（注意，必须是非负整数）统一为位数相同的整数，位数较少的前面补零。一般用10进制，
2. 也可以用16进制甚至2进制。所以前提是能够找到最大值，得到最长的位数，设 k 进制下最长为位数为 d 。
3. 从最低位开始，依次进行一次稳定排序。这样从最低位一直到最高位排序完成以后，整个序列就变成了一个有序序列。

下面是例子
有一个整数序列，0, 123, 45, 386, 106，下面是排序过程：
第一次排序，个位，0 3 5 6 6
第二次排序，十位，00 06 23 45 86
第三次排序，百位，000 045 106 123 386
最终结果，0, 45, 106, 123, 386, 排序完成。

注意同一数位的排序子程序要用稳定排序，因为稳定排序能将上一次排序的成果保留下来。

---

如何实现一个通用的、高性能的排序函数

如何优化快速排序
O(n2)时间复杂度出现的主要原因是因为我们分区点选的不够合理。

最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。

作者给出的两种方法：

1.三数取中法
我们从区间的首、尾、中间，分别取出一个数，然后对比大小，取这3个数的中间值作为分区点。这样每间隔某个固定的长度，取数据出来比较，将中间值作为分区点的分区算法，肯定要比单纯取某一个数据更好。但是，如果要排序的数组比较大，那“三数取中”可能就不够了，可能要“五数取中”或者“十数取中”。
2.随机法
随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好，但是从概率的角度来看，也不大可能会出现每次分区点都选的很差的情况，所以平均情况下，这样选的分区点是比较好的。时间复杂度退化为最糟糕的O(n2)的情况，出现的可能性不大。

同时鉴于用了递归的快排存在内存栈溢出的风险，
作者给出的两种方法：

1.限制递归深度。一旦递归过深，超过了我们事先设定的阈值，就停止递归。
2.在堆上模拟实现一个函数调用栈，手动模拟递归压栈、出栈的过程，这样就没有了系统栈大小的限制。

作者分析了一波C语言中的排序函数qsort()
qsort()先判断了一下数据量

1. 当数据量非常小（指小于等于4时），qsort()会进行插入排序，且使用了哨兵来减少if的判断，将性能优化至极致。
2. 当数据量较小时，此时即使多耗费一倍内存去开辟临时数组也不会有太多影响，但是可以保证时间复杂度稳定在O(nlogn)。
3. 最后，才会选择使用快速排序，且选择分区的方法是前面提到的“三数取中法”，对于递归会太深的问题也是通过自己实现一个堆上的栈，手动模拟递归来解决的。

为什么qsort()会使用插入排序？它不是O(n^2)的复杂度吗？
作者的解答是：
在大O复杂度表示法中，我们会省略低阶、系数和常数，也就是说，O(nlogn)在没有省略低阶、系数、常数之前可能是O(knlogn + c)，而且k和c有可能还是一个比较大的数。

假设k=1000，c=200，当我们对小规模数据（比如n=100）排序时，n2的值实际上比knlogn+c还要小。

knlogn+c = 1000 * 100 * log100 + 200 远大于10000

n^2 = 100*100 = 10000

看来，也不能盲目认为O(nlogn)的就是优于O(n^2)的，没有绝对好的算法，只有最合适当前场景的算法