【矩阵论】矩阵的相似标准型(2)
矩阵的相似标准型之Hamilton-Cayley定理
在该系列第一篇文章中的末尾我们讲到可以利用矩阵的化零多项式来求解矩阵的候选特征解,这一篇文章我们就要讨论矩阵的化零多项式是否一直存在的问题。
一. Hamilton-Cayley定理
1. 矩阵表述
将矩阵A代入A的特征多项式中,得到的应该是一个零矩阵O。
此处老师未给出详细证明,可以借助等下要讲的Schur引理进行证明。
但是这里要规避一个错误的证明思路
C(A) = |A·I-A| = |A-A| = |O| = 0
其一,C(λ)是一个多项式,对一个矩阵进行多项式运算,最终得到也应该是一个矩阵,而不是行列式
其二,定理中的结论最终的结果应该是一个零矩阵,但是上述证明过程中得到的结果是数值0.
以上证明思路是错误的!!!
2. 线性变换表述
前几节花了很大篇幅讨论了线性变换 f 和矩阵A之间是具有某种等价关系的,那么恶意很自然地把矩阵A的这个关系定理延伸到线性变换f上。
3. Schur引理
![]()
再回顾一遍,酉矩阵U是满足UH·U = I(也就是UH = U-1)关系的矩阵
证明采用数学归纳法的思想,对A所属的内积空间Cnxn的维度进行归纳.
step 1:当k = 1时,A就是一个数域为C中的一个数,自然可以看成是一个上三角矩阵(U = I即可)
step 2:假设当k = n-1时结论成立,即对于任意一个A∈Cn-1xn-1,存在酉矩阵U使得UH·A·U 是上三角矩阵
step 3:现在考虑当k = n时,上述结论是否成立
内心OS:老师的证明真的是特别出彩,每次听老师讲证明的时候都会梦回小学奥数题现场,因为老师总会有一些巧妙的好用的但是你自己就是想不出来的奇妙思路突破口。
【奇奇妙妙小结论】
对于Cnxn空间中的任意一个矩阵,其一定存在特征值。
因为该矩阵的特征多项式|λI-A|是复数范围内的一个多项式,根据代数知识,在复数域求解多项式方程式一定有解的。
不妨设λ0是A的一个特征值,ω是A相应于特征值λ0的一个单位特征向量
【奇奇妙妙小结论】
对应于某一特征值的特征向量都可以进行单位化。
按照特征量的定义,对于矩阵A,如果满足Aω = λω,就可以说λ是A的特征值,而ω是A相应于λ的一个特征向量。
且我们也知道,矩阵对应于一个特征值的特征向量是不唯一的。
我们可以对上述等式两边同时除以向量ω的模长,即:Aω·(1/||ω||) = λω·(1/||ω||)
既然ω是一个Cn中的一个单位向量,那么我们可以把该向量进行扩充成(ω,ω2,…,ωn),形成Cn空间中的一组标准正交基,构成矩阵Q = (ω,ω2,…,ωn)。
接下来我们需要考察QH·A·Q的矩阵形态是什么样的,先只看该矩阵的第一列,也就是构造一个列向量e1 = (1,0,0…,0),计算QH·A·Q·e1即能得到结果矩阵的第一列。
矩阵的乘法运算满足结合律,则上式可以按照QH·A·(Q·e1)的顺序进行运算,Q·e1运算得到的就是矩阵Q的第一列,也就是ω向量,所以QH·A·Q·e1 = QH·A·ω。
又因为ω是矩阵A的特征向量,按照Aω = λ0ω,则有QH·A·Q·e1 = QH·A·ω = λ0QH·ω
QH这个矩阵可以进行分块拆解成[ωH,ω2H,…,ωnH]T的形式,按照分块矩阵的运算规则,计算出了矩阵第一列的形式

在第一行要进行ωH·ω的运算,第二行要进行ω2Hω的运算,以下以此类推。
又因为这些向量都是定义在Cn空间中的,所以形如ωH·ω的运算式实质是在计算两向量之间的标准内积。
根据以上的计算,可以把QHAQ写成一个2x2的分块矩阵[[λ0,],[θ,B]]的形式,其中表示含有若干元素,θ表示全零元素,B表示一个n-1阶的矩阵。
因为B是n-1阶的矩阵,所以存在一个酉矩阵Q1,使得Q1HBQ1 = T,其中T是一个上三角矩阵(step2中的假设)
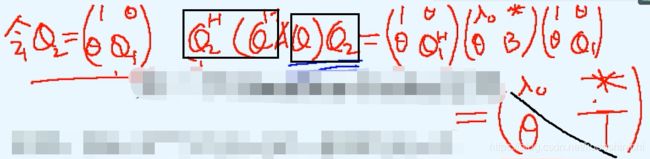
根据上图的计算,就会发现如果令U = Q·Q2,那么U是一个酉矩阵,且能够上述分块矩阵的运算得到UH·A·U是一个上三角矩阵,故证毕。
Q是一个酉矩阵,是因为Q就是由Cn中的一组标准正交基构成的。
Q2是一个酉矩阵,是因为按照上图,Q2是由两个酉矩阵构成的分块对角矩阵。
计算到这里,可以自己总结一些小结论:
- 有限个酉矩阵构成的分块对角阵也是酉矩阵
- 酉矩阵的乘积也是酉矩阵
p.s. 按照酉矩阵的定义很容易可以证明~
【Schur定理那些事】
前面说过了Schur引理对于证明Hamilton-Cayley定理以及后续的一些应用很有用,它对于求解特征量也同样有用。
因为酉矩阵U满足UH = U-1,所以UHAU是一个上三角矩阵,也就等价于U-1AU是一个上三角矩阵,也就是说对于任意一个A都可以相似于一个上三角阵。
上三角阵的特征值很显然就是矩阵的主对角线元素。
二. 在矩阵计算上的应用
1. 求解矩阵高次幂
在线性代数中,碰到要求一个矩阵的高次幂,我们通常采用相似对角化,因为对角阵的运算有规律可循。
问题的关键就是找到相似变换矩阵P和对角阵Λ
但是并不是每一个矩阵都能够进行相似对角化,以下就讲解利用Hamilton-Cayley定理求解高次幂的方法
[1]:把矩阵A的特征多项式先写出来并且化成两点式,为后续求解参数做准备。
[2]:因为我们要求的是A1000,本质就是要对矩阵A进行多项式运算,也即构造一个多项式f(λ) = λ1000,代入A计算f(A)即可。
因为我们有一个二次多项式C(λ),所以我们想要把λ1000用C(λ)以及余项进行表示
用C(λ)进行表示,就是想要利用Hamilton-Cayley定理中C(A) = O的特点。
上图2号框中,q(λ)就是进行多项式除法的商,aλ+b就是除法的余项
因为除数C(λ)是一个二次多项式,所以余项最高次也只有1次。
代入A之后,上式第一项为0,因此我们只关注a和b两个未知参数的值。
[3]:这个时候1处进行的运算就派上用场了,利用C(λ)的两个零点来求解a和b两个未知参数,计算量减少了很多!!!
[4]:最后将A代入,a和b用计算出来的值替代,就得到A1000的结果。
因为具体的求解思路和例一是完全一致的,所以下面只简单列写计算过程,不对原理进行讲解,计算结果也不再写出。

因为求解特征方程C(λ) = 0只能得到两个根,-1和1,其中λ = -1是二重根。
但是我们在对λ100进行多项式分解的时候,因为C(λ)是三次多项式,所以余项是形如aλ2+bλ+c的二次式,需要确定三个未知参数;但仅有的两个特征根只能写出两个方程,是无法确定三个未知参数。
这时候就要利用到重根的性质。
λ = -1是二重根,也就是(λ+1)项在C(λ)中出现了两次,那么自然在λ100中的C(λ)q(λ)中也出现了两次,如果式子两边关于λ求一次导,那么(λ+1)2求导后变成2(λ+1),依然含有一次(λ+1),所以求导后代入-1,依然可以使得C(λ)q(λ)这一项为零,从而得到第三个方程。
如果特征方程求解出来后存在k重特征根,那么就对多项式求解k-1次导。
2. 最小多项式
我们讨论 Hamilton-Cayley定理,是因为该定理能够保证一个矩阵的化零多项式一定存在。
除去存在性问题,我们还希望化零多项式的形式能够尽可能地简单,次数能够尽可能地低。
e.g. 比如在求矩阵高阶项的时候,特征多项式C(λ)就是矩阵的化零多项式,而我们是借助C(λ)对高阶多项式进行分解,如果C(λ)是k次幂的多项式,那么我们最后实质上只需要确定一个k-1阶的多项式,就能完全求出矩阵的高次幂。
至此,最小多项式的概念应运而生。
(1)定义
矩阵A的次数最低的、最高次项系数为一的化零多项式称为A的最小多项式。
(2)性质
【证明】
假设m(x)不能整除φ(x),那么就能得到等式【φ(x) = m(x)q(x)+r(x)】,其中q(x)是多项式的商,r(x)是多项式的余数,且如果r(x)≠0,那么一定有r(x)的次数比m(x)的次数低。
接下来把矩阵A代入到上述等式中去,左边有φ(A) = O——化零多项式的定义。
右边有m(A)q(A)+r(A) = O+r(A) ——最小多项式也是化零多项式。
左边 = 右边,即得到r(A)= O,就说明r(x)也应该是一个化零多项式,且r(x)的次数比m(x)小。
这一点与题干中所说的m(x)是最小多项式产生矛盾,不符合最小多项式中“次数最低”的定义。
②最小多项式的唯一性
Tip 1:一般给出一个数学定义,确定了其存在性之后,都会考虑一下它的唯一性。
Tip 2:唯一性在证明的时候一般都是采用反证法。
【证明】
假设对于一个矩阵A,存在两个最小多项式,分别记为m1(x)和m2(x),其二者既然是最小多项式,那么肯定也是化零多项式,那么其二者就可以相互整除。
p.s. 这里我觉得“相互整除”就已经可以推断出m1(x)=m2(x)了,因为如果m1(x)能被m2(x)整除,就应该有m1(x) = km2(x);反之,m2(x)能被m1(x)整除,就应该有m2(x) = tm1(x);根据运算关系,k和t应该是互为倒数且均为整数,那么只可能是k = t = 1的情况。
按照老师的证明,其二者可以相互整数,那么就说明它们之间存在倍数关系m1(x) = k*m2(x),又因为最小多项式要求最高次项系数为1,所以这里k只能为1.
p.s. 可以认为上面两种思路都共同约束了倍数系数只能为1的事实。
于是,我们常把某一矩阵A对应的最小多项式记作mA(x)
③两个相似矩阵具有相同的最小多项式(化零多项式)
【证明】
[1]:两个矩阵相似所具有的对应关系
[2]:如果存在一个多项式,那么两个矩阵的多项式运算也具有某种对应关系,其中P是一个可逆矩阵。
[3]:该多项式是A的化零多项式的充要条件就是该多项式同样也是B的化零多项式。
两个矩阵既然具有相同的化零多项式,那么进行同样的降幂、最高阶项化为1的操作之后,得到的夜视相同的最小多项式。
(3)定理——最小多项式和特征多项式之间的代数关系

其一,m(x)|C(x),最小多项式能够整除特征多项式,显而易见。因为根据Hamilton定理,C(A) = O,特征多项式就是矩阵A的一个化零多项式,根据上面的性质,可以得到最小多项式是可以整除化零多项式的。
其二,最小多项式和特征多项式具有相同的零点。
【证明】
必要性,因为m(λ0) = 0,也因为m(x)和C(x)之间具有整除关系,所以C(x)可以写成关于m(x)的因式乘积,故m(x)的零点必要也是C(x)的零点。
充分性,若有C(λ0) = 0,那么说明λ0是矩阵A的一个特征值,根据化零多项式的定理,矩阵A的特征值都是化零多项式的零点,但化零多项式的零点不一定都是特征值。
p.s. 有关化零多项式的详细讨论请见《【矩阵论】矩阵的相似标准型(1)》中有关化零多项式的部分。
该充要条件实质上是告诉我们,不考虑根的重数时,最小多项式和特征多项式具有相同的零点。

上图中的1≤tj≤cj这个关系式就体现了定理的两个方面:
tj≥1,因为它们具有相同的根;
tj≤cj,因为最小多项式可以整除特征多项式。
虽然最小多项式是化零多项式中次数最低的,但并不意味着t1-ts就一定只能取1.
【例】最小多项式的求解 - 1
通过例一,我们需要明白:
虽然特征多项式可以把最小多项式确定到某个范围之内,但是最小多项式并不能由特征多项式唯一地确定,还需要考虑实际矩阵情况。

上述矩阵是上三角阵,因此其三者的特征多项式都是C(λ) = (λ-a)3;但是其三者的最小多项式全不相同。
这里关于最小多项式怎么求解,弹幕中看到了一句【假设-验证】我觉得目前来说是可用的。
我们知道最小多项式一定是特征多项式的因子式,那就说明最小多项式只可能是(λ-a)i,其中i = 1,2,3,找到各个矩阵所能取到的最低次幂就得到了最小多项式。
p.s. 当然也是因为这个例题比较简单,特征多项式只有一个因子,所以可以蛮力验证。
【例】最小多项式的求解 - 2
这个例题似乎比较考察分类讨论的能力,当然在求解过程中,对于化零多项式、最小多项式以及特征多项式之间的关系也会有更深刻的把握。

首先,回顾一下在《【矩阵论】矩阵的相似标准型(1)》中我们求解过的这个矩阵的特征多项式C(λ) = λn-1(λ-<α,β>),涉及到λ = 0是多少重根的问题,我们需要对α和β是否正交进行讨论。
其一,当α与β不正交时:
我们能够想到的最低阶的最小多项式可能的形式就是 λ(λ-<α,β>),接下来我们只需要验证该多项式是否为化零多项式。

上图中对A2进行计算,根据矩阵乘法的结合律,能够得到A2 = <α,β>·A的等式,从而就说明了λ(λ-<α,β>)是化零多项式,也就是我们所要求的最小多项式。
其二,当α与β正交时:
特征多项式C(λ) = λn,那么可能的最小多项式的形式就是λi,其中i=1,2,3…n。
我们依然从最低阶i =1开始验证其是否可以化零。
对于λ这个项是否可以化零取决于A是否为零矩阵,因此需要进行进一步分类讨论。
当α或β中存在一个零向量时,那么A就是零矩阵,从而mA(x) = x;
当α和β都不为零向量时,那么A就不是零矩阵,从而根据A2 = <α,β>·A的等式可以确定A2 = O,mA(x) = x2。
【补充】-“当α和β都不为零向量时,那么A就不是零矩阵”的理解
- 考虑αβH中的(i,j)元素,应该为αi·bjH,如果α和β都是非零向量,那么至少能够找到一个这样的非零元,使得矩阵为非零阵;
- 从矩阵的秩来说,r(αβH)≥r(α)+r(βH)-1 = 1,所以一定是非零矩阵。
p.s. 减去1是因为α的列数和βH的行数均为1,这是矩阵秩的性质。
在这一节我们只是来认识一下最小多项式是一个怎么样的多项式,后续最小多项式对于矩阵的线性变换以及性质讨论都有很大作用,读者需要熟悉这一概念。