正睿OI补题(二分与分治)
二分与分治
目录:
二分:
P2440 木材加工
P1577 切绳子
P2678 [NOIP2015 提高组] 跳石头
分治:
P1228 地毯填补问题
CF1400E Clear the Multiset
P2440 木材加工
P2440 木材加工 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:直接二分即可,得算出能分成几段,然后比较这个段数与计划段数的大小
#include
#include
#include
using namespace std;
const int N = 1e5+10;
int L[N];
int n,k;//n表示原木的数量,k表示小段的数量
int main()
{
cin>>n>>k;
for(int i = 1;i <= n;i++)
{
cin>>L[i];
}
int l = 0,r = 0x3f3f3f3f;
while(l+1 < r)
{
int mid = (l+r)>>1;
int cnt = 0;
for(int i = 1;i <= n;i++)
cnt += L[i]/mid;
if(cnt >= k) l = mid;
else r = mid;
}
cout< P1182 数列分段 Section II
P1182 数列分段 Section II - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:在实现的过程我们可以采用前缀和的思想,但是在这一题中我们可以用贪心的思想来解决
Ps:在这题的l要定义为大一点的那个数,因为我们需要输出的就是最大值,l刚好对应最小值
//P1182
//思路:题目中说要求最大值最小,所以果断套用二分模板
#include
using namespace std;
const int N = 100010;
int a[N];
int n,m,l,r;
bool check(int x)
{
int tot = 0,sum = 0;
for(int i = 1;i <= n;i++)
{
if(tot+a[i] <= x)tot += a[i];
else tot = a[i],sum++;//sum表示数哦,sum++意味着选择下一个数进行累加
}
return sum>=m;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++)
{
cin>>a[i];
l = max(l,a[i]);
r += a[i];
}
while(l <= r)
{
int mid = (l+r) >> 1;
if(check(mid))l = mid+1;//分段数 > 指定分段次数 , 说明指定的和太小,应该让和大点,才能让分段次数少点,因此进入右区间left = mid + 1
else r = mid-1;
}
printf("%d",l);
return 0;
} P1577 切绳子
P1577 切绳子 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
//P1577
//思路:也是直接二分即可
#include
using namespace std;
const int N = 100010;
double d[N];
int a[N];
int n,m,mxn,mn;
bool check(int x)
{
int tot = 0;
for(int i = 1;i <= n;i++)
tot += a[i]/x;
return tot>=m;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++)
{
cin>>d[i];
a[i] = (int)(d[i] * 100);
}
int l = 0,r = 0x3f3f3f3f;
while(l <= r)
{
int mid = (l+r) >> 1;
if(mid == 0)break;//0不能作为除数
if(check(mid))l = mid+1;//分段数 > 指定分段次数 , 说明指定的和太小,应该让和大点,才能让分段次数少点,因此进入右区间left = mid + 1
else r = mid-1;
}
printf("%.2f",r / 100.0);
return 0;
} P2678 [NOIP2015 提高组] 跳石头
P2678 [NOIP2015 提高组] 跳石头 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:从位置的小到大扫遍所有石头,用一个变量存储上一个跳到的点。第一个与这上一个点的距离大于等于x的石头即是下一个跳到的点。这里用了一点贪心的思想:因为如果不跳到第一个符合条件的点上,那么整个队列的稀疏度就会提高,最终需要删除的石头也会更多。因为我们要取最优状态,所以要保证跳过的石头数最少。当然,如果某个石头到终点的距离小于x,那它不能被统计到——所以得删去后面这些无法跳到的石头。(我就是少特判了这个玩意WA了好久)
//P2678
#include
using namespace std;
const int N = 5e5+10;
int d,n,m,ans;
int a[N];
bool check(int x)
{
int sum = 0,tot = 0;
for(int i = 1;i <= n;i++)
{
if(a[i] - tot < x)sum += 1;//表示被搬走石头的数量叠加
else tot = a[i];
}
if(d-tot < x)sum+=1;//关键部分!!!!!警钟敲烂
return sum <= m;
}
int main()
{
scanf("%d%d%d",&d,&n,&m);
for(int i = 1;i <= n;i++)
{
cin>>a[i];
}
sort(a+1,a+1+n);
int l = 0,r = d;
while(l <= r)
{
int mid = (l+r)>>1;
if(check(mid))
{
ans = mid;
l = mid+1;
}
else r = mid - 1;
}
printf("%d",ans);
return 0;
} P1228 地毯填补问题
P1228 地毯填补问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
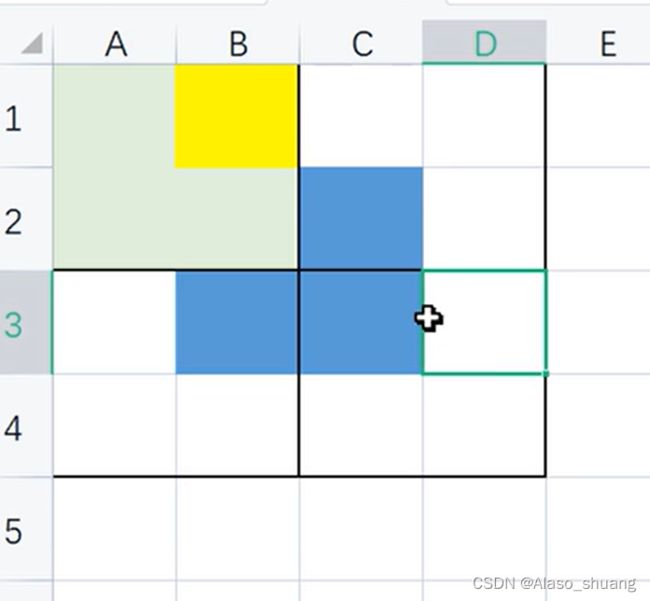
思路:
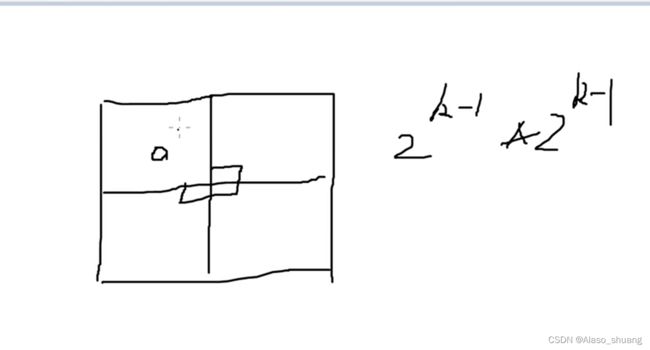
看图说话,一个2^k的可以分为2 ^ (k-1)的子问题
找规律按照下图直接写代码即可!!!
我真的会谢!把l打成1的低级错误!!
//P1228
#include
using namespace std;
void f(int x,int y,int gx,int gy,int l)
{
if(l == 1)return;
//先要确定障碍物在哪个区块
//在这个区块的对应角放上一个障碍物
//将原来的大块分为4个小块递归调用f
if(gx <= x+l/2-1 && gy <= y+l/2-1)
{
//左上角
cout<= y+l/2)
{
cout<= x+l/2 && gy <= y+l/2-1)
{
cout<= x+l/2 && gy >= y+l/2)
{
cout<>k>>x>>y;
f(1,1,x,y,pow(2,k));//(x,y)表示公主的坐标,pow(2,k)表示矩阵的大小 2^k的长度
return 0;
} CF1400E Clear the Multiset
CF1400E Clear the Multiset - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:题目说了要按两种操作
用操作一时:我们的 f(l,x-1)+f(x+1,r)+k
不用操作一的时候我们的最小操作次数是 r - l +1
最后 我们两者综合起来取最小值即可
答案是f(1,n)
上代码!!
//CF1400E
#include
using namespace std;
const int N = 5050;
int n;
int a[N];
int f(int l,int r)
{
if(l > r) return 0;
if(l == r)return min(a[l],1);
int k = 0x3f3f3f3f;
int x;
for(int i = l;i <= r;i++)if(k > a[i]) k = a[i],x = i;
for(int i = l;i <= r;i++)a[i] -= k;
return min(r-l+1,f(l,x-1)+f(x+1,r)+k);
}
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>a[i];
}
int cnt = f(1,n);
cout<