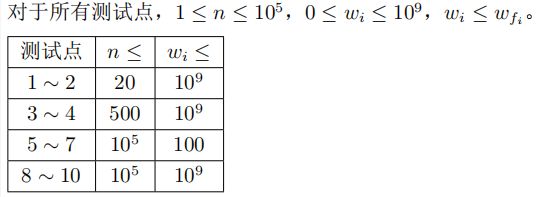NOIP2022广东省选day1题解

                                                             T1 邹忌讽齐王纳谏

齐国人邹忌对齐国国君齐威王说，大王身边的人会因为私情、利益等原因而对大王阿谀奉承，所以不能光听好话，只有广泛接受群众的批评意见，才不会被蒙蔽双眼，齐国才能强盛。齐威王接受了这个意见，于是昭告全国：
1. 如果有臣民当面对齐威王提出建议，则获得价值为 A 的奖励；
2. 如果有臣民以书信的方式对齐威王提出建议，则获得价值为 B 的奖励；
3. 如果有臣民在街市中议论齐威王，意见流传到宫廷，则获得价值为 C 的奖励。
你通过史书整理出了某一年的建议记录，按时间顺序罗列，共有 n 条，每条记录形如”name way”，其中 name 是由小写英文字母组成的字符串（由于博物馆的计算机太古老了，只支持英文，所以你也只能用英文做记录），表示提建议者的名字；way 是一个为 1、2 或 3 的数字，表示提建议的方式。你发现记录中有些人提出了多次建议，从而获得多次奖励，因此你很好奇这些人之中获得奖励总和最多的是谁，他总共获得了多少奖励。如果获得最多奖励的不止一个人，请输出最早获得最多奖励的人。 

输入
第一行四个整数 n, A, B, C，表示建议记录的数量和三种建议方式的奖励价值。
接下来 n 行，每行一个字符串 name 和一个数字 way，用空格隔开，表示一条建议记录。 

输出
一行，一个字符串 name 和整数 v，用空格隔开，表示名字为 name 的人总共获得了 v 的奖励。他是获得奖励总量最多并且最早获得这么多奖励的人。 

样例输入
5 30 20 10
zzz 2
wh 1
lh 3
wh 2
zzz 1 

样例输出
wh 50 
 

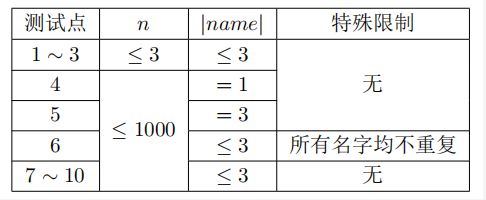
数据范围限制
对于所有测试点，0 ≤ A, B, C ≤ 1000，1 ≤ n ≤ 1000，1 ≤ |name| ≤ 3。

提示
记录共有 3 人，其中 lh 获得了 10 的奖励，zzz 和 wh 都获得了 50 的奖励，但 wh 完全获得 50 奖励的时间比 zzz 早。 

代码如下

#include
using namespace std;
mapa;
int n,b[3],w,ans;
string s,anss;
int main(){
	cin>>n>>b[0]>>b[1]>>b[2];
	for(int i=1;i<=n;i++){
		cin>>s>>w;
		a[s]+=b[w-1];
		if(ans

                                                               T2 数列游戏

有一个长度为 n 的序列 a1, · · · , an。如果序列的长度大于 1，那么你就能进行操作，每次操作可以选择两个相邻的数 ai , ai+1 合并，得到一个新的数 ai ⊕ ai+1（“⊕”表示异或），每次操作都会使序列的长度减少 1。例如对将序列 [8, 3, 5, 7, 1] 中的第 2个和第 3 个数进行合并，会得到新序列 [8, 6, 7, 1]，并可以进行下一轮操作。你需要进行若干次操作（可能是 0 次），使得最终序列任意子区间的异或和不为 0。子区间的定义为连续的一段数 [al , al+1, · · · , ar]（l ≤ r）。求满足条件的最终序列的最长长度。 

输入
第一行一个正整数 n，表示序列长度。
第二行 n 个正整数 a1, · · · , an，表示序列。

输出
一个整数，满足条件的最终序列的最长长度。如果不存在这样的序列则输出“-1”（不含引号）。

样例输入
4
5 5 7 2 

样例输出
2 

数据范围限制
 

提示
一种方案是先选择 a1, a2 合并，得到 [0, 7, 2]，再选择前两个数合并，得到 [7, 2]。不存在方案使得最终序列长度为 3 或 4。

代码如下

#include 
using namespace std;
mapm;
int n, a, s, t;

int main() {
	cin >> n >> a;
	s = a;
	for (int i = 1; i < n; i++) {
		cin >> a;
		s ^= a;
		if (m[s] == false) {
			m[s] = true;
			t++;
		}
	}
	cout << t ;
	return 0;
}

补充 ：懒着打-1的点，可以自己不上

                                                             T3 流水线

在计算机组成原理这门课中，小明的老师布置了实现 CPU 流水线的作业。小明打算设计出一个效率最高的流水线。简单来说，流水线就是将 CPU 分成若干个任务模块，而一个模块又可以继续划分成更小的模块，小模块可以划分成更小的小小模块……根据常识我们知道把一个任务划分后，每一个部分的代价会变少，但是可能会产生额外的代价。所以小明希望你帮助他解决这个问题。
我们可以用一棵以 1 为根的有根树来描述模块之间的关系，每个节点是一个模块，每个节点的点权对应着该模块的时间代价。每一个非叶子节点可以划分成该节点的儿子节点对应的模块。
每个模块都有一定的时间代价，而流水线最后的效率我们可以用划分的模块数乘上模块中时间代价最大的一个来表示，时间代价越小，流水线的效率越高。也就是说，假如小明最后把 CPU 划分为了 m 个模块，每个模块的代价为 w1, w2, · · · , wm，则总代价为 m · max(w1, w2, · · · , wm)。另外，我们认为根节点对应的模块
不往下划分模块也是一种合法的方案。
请你帮小明找到效率最高的流水线设计方案吧 

输入
第一行一个正整数 n，表示模块对应有根树的节点个数。
第二行 n 个整数，表示 n 个模块的时间代价 wi。
第三行 n − 1 个数 fi（2 ≤ i ≤ n），表示节点 2, · · · , n 在有根树中的父节点。保证给出的是一棵以 1 为根的树。 

输出
一个整数 T，表示最小的时间代价。 

样例输入
5
10 7 3 3 2
1 1 2 2 

样例输出
9 

数据范围限制
  

提示
样例中将模块 1 拆分为模块 2 和模块 3，再将模块 2 拆分为模块 4 和模块 5，代价为 3 · 3 = 9。

代码如下

#include 
using namespace std;
const int N = 1000010;
long long n, m;
int a, b, i, j, k, v[N], h[N], t, p;

struct AB {
	int a, b, n;
} d[N];

struct tt {
	int i, v;
};

bool operator < (tt x, tt y) {
	return x.v < y.v;
}
priority_queue q;

int main() {
	cin >> n;
	for (i = 1; i <= n; i++)
		cin >> v[i];
	for (i = 2; i <= n; i++) {
		cin >> a;
		d[i].a = a;
		d[i].b = i;
		d[i].n = h[a];
		h[a] = i;
	}
	q.push(tt{1, v[1]}), m = v[1];
	while (n = q.size()) {
		t = q.top().v;
		p = q.top().i;
		q.pop();
		m = min(m, t * n);
		if (!h[p])
			break;
		for (i = h[p]; i; i = d[i].n)
			q.push(tt{d[i].b, v[d[i].b]});
	}
	cout << m;
	return 0;
}

                                                             T4 小学生计数题

作为 GDOI 的组题人，小 Y 需要整理手中已有的题目，考虑它们的难度以及所考察的知识点，然后将它们组成数套题目。小 Y 希望先能组出第一套题目，为了整套题目具有良好的区分度，在一套题目中：
• 所有题目的难度需要能排成等差数列；（也就是说，若将所有题目按难度从小到大排序，那么每相邻两题的难度的差相等，这个差叫做公差）
• 每道题目的难度都是公差的倍数，公差不为 0；
• 需要有不少于 L 道题，不多于 R 道题。
现在小 Y 手里已经有了 m 道题目，其中难度为 ai 的题有 ci 道（1 ≤ i ≤ n）。小 Y 希望能够知道，他有多少种不同的方式能够组出一套题目。
在这道题目中，我们认为两种组题方式不同当且仅当 ∃k(1 ≤ k ≤ m)，使得一种方案包含第 k 道题而另一种方案不包含。由于答案可能很大，输出答案对 998244353 取模。

输入
第一行三个整数 n, m, L, R，分别表示有多少种不同难度的题目、题目总数、一套题的题数下限和上限。
接下来 n 行，每行两个正整数 ai , ci，表示有 ci 道难度为 ai 的题（1 ≤ i ≤ n）

输出
输出一个数，表示组题方案数对 998244353 取模的值

样例输入
6 12 2 3
2 2
4 2
6 2
8 2
12 2
16 2

样例输出
64 

数据范围限制
 

这题真就感觉是清华大学附属小学的题

代码如下

#include
using namespace std;
const int N=100005,mo=998244353;
int n,m,i,j,k,x,y,c[N];
long long a[N],b[N],s[N],t[N],ans;
int mi(long long a,long long b){
    int s=1;
    while(b){
        if(b&1) s=s*a%mo;
        a=a*a%mo,b/=2;
    }
    return s;
}
void cal(){
    if(!n) return ;
    int i,j,k,p;
    b[0]=t[0]=1;
    for(i=1;i<=n;i++){
        b[i]=b[i-1]*a[i]%mo;
        s[i]=s[i-1]+b[i];
        t[i]=mi(b[i],mo-2); 
    }
    for(i=x,j=y,p=0;i<=n;i++,j++,p++){
        if(j>n) j=n;
        ans+=(s[j]-s[i-1])%mo*t[p]%mo;
    }
    n=0,ans%=mo;
}
int main(){
    scanf("%d%d%d%d",&i,&n,&x,&y);
    while(i--){
        scanf("%d",&k);
        scanf("%d",&c[k]);
        m=max(k,m);
    }
    for(i=1;i<=m;i++){
        for(n=j=0;j<=m;j+=i){
            if(!c[j]) cal();
            else a[++n]=c[j];
        }
        cal();
    }
    printf("%lld\n",ans);
}