回归预测鲍鱼年龄案例
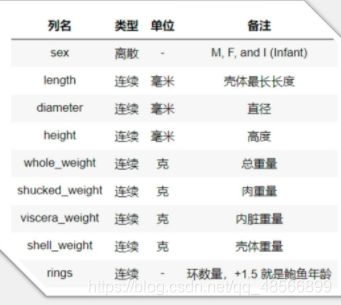
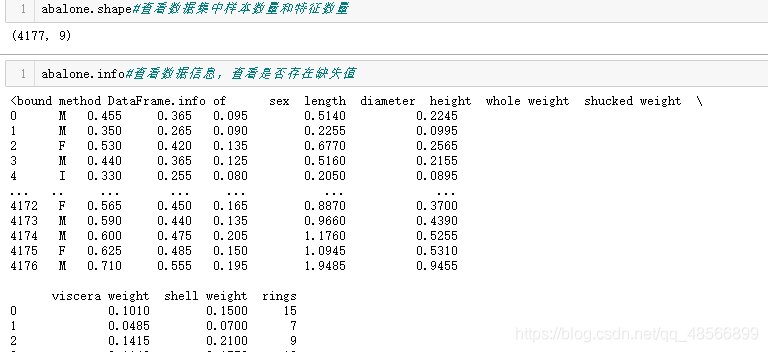
了解鲍鱼数据
https://archive.ics.uci.edu/ml/datasets/Abalone
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
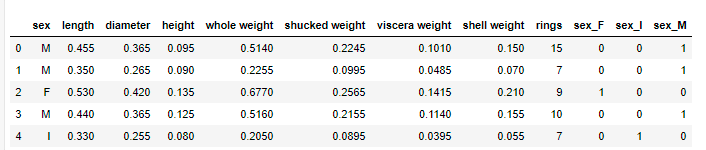
abalone=pd.read_csv("abalone_dataset.csv")
abalone.head()

对于连续特征,可以使用seaborn的distplot函数绘制直方图观察特征数取值情况,我们将8个连续特征的直方图绘制在一个4行2列的子图布局中。
import matplotlib.pyplot as plt
import seaborn as sns
#观察各个特征分布
i=1#子图技术
plt.figure(figsize=(16,8))
for col in abalone.columns[1:]:
plt.subplot(4,2,i)
i=i+1
sns.distplot(abalone[col])
plt.tight_layout()
![]()
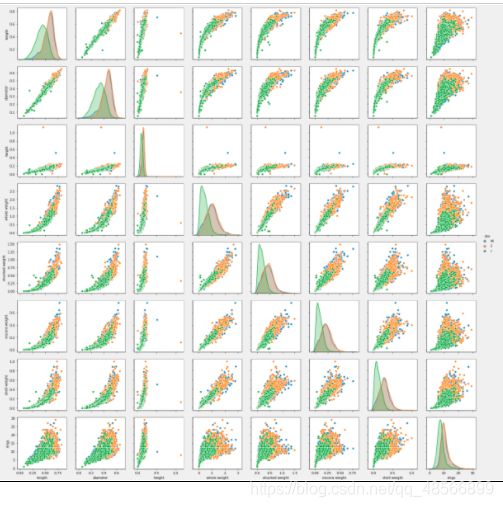
有上图可知
有第一行知道length,diametwe,height存在明显的线性关系,鲍鱼长度与鲍鱼的四种重量之间存在明显的非线性关系
有最后一行知道,rings和各个特征之间均存在正相关,其中与height的线性关系最为直观。
观察对角线上的直方图,可以看见sex=i在各个特征上的取值明显小于sex=m,f的成年鲍鱼。而m与f各个特征分布没有明显的差别。
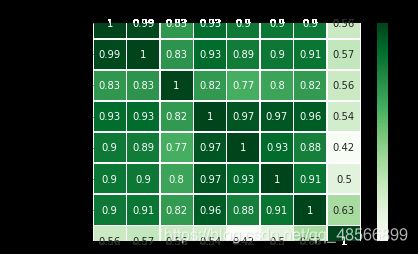
为了定量地分析特征之间的线性相关性,我们计算特征之间的相关系数矩阵,并借助热力图将相关性可视化
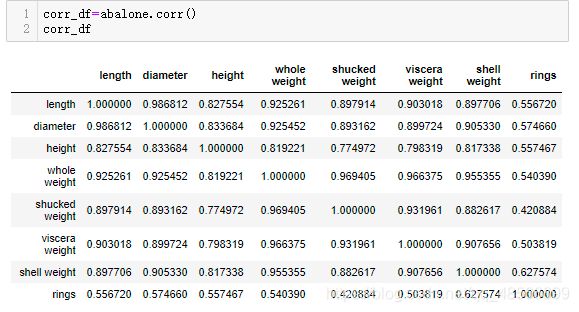
fix,ax=plt.subplots(figsize=(12,12))
# 绘制热力图
ax=sns.heatmap(corr_df,linewidths=.5,
cmap='Greens',annot=True,xticklabels=corr_df.columns,
yticklabels=corr_df.index)
ax.xaxis.set_label_position('top')
ax.xaxis.tick_top()
数据预处理
sex进行onehot编码
# 数据预处理
#对sex进行onehot编码,便于后续模型纳入哑变量
sex_onehot=pd.get_dummies(abalone['sex'],prefix='sex')
abalone[sex_onehot.columns]=sex_onehot
abalone.head()
添加取值为1的特征
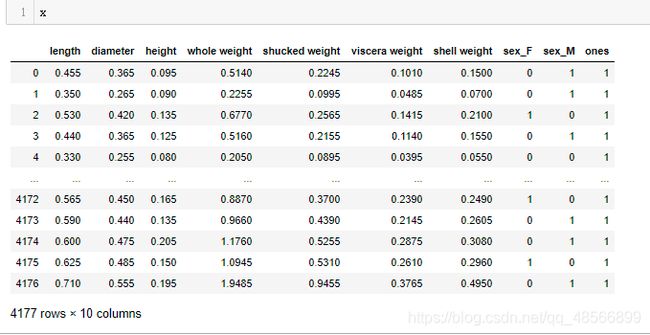
#添加取值为1的特征
abalone['ones']=1
abalone.head()
根据鲍鱼环计算年龄
# 根据鲍鱼环计算年龄
abalone['age']=abalone['rings']+1.5
abalone.head()
筛选特征
y=abalone['age']
features_with_ones=['length','diameter','height','whole weight','shucked weight','viscera weight','shell weight','sex_F','sex_M','ones']
features_without_ones=['length','diameter','height','whole weight','shucked weight','viscera weight','shell weight','sex_F','sex_M']
x=abalone[features_with_ones]
划分数据集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=111)
线性回归&岭回归
线性回归
使用numpy实现线性回归

np.dot矩阵相乘
np.linalg.inv矩阵的逆
np.linalg.det矩阵行列式
import numpy as np
#能否算w ,需要判断是否可逆
def linear_regression(x,y):
w=np.zeros_like(x.shape[1])
if np.linalg.det(x.T.dot(x))!=0:
w=np.linalg.inv(x.T.dot(x)).dot(x.T).dot(y)
return w
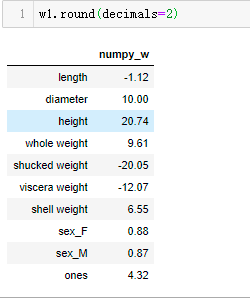
w1=pd.DataFrame(data=w,index=x.columns,columns=['numpy_w'])
sklearn 调包实现线性回归
from sklearn.linear_model import LinearRegression
lr=LinearRegression()
lr.fit(x_train[features_without_ones],y_train)
print(lr.coef_)
[ -1.118146 10.00094599 20.73712616 9.61484657 -20.05079291
-12.06849193 6.54529076 0.87855188 0.87283083]
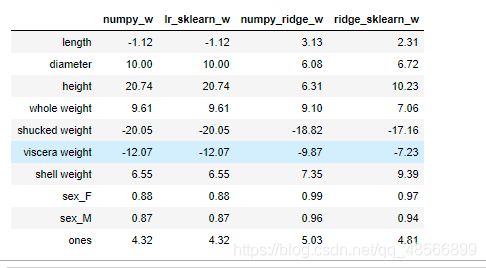
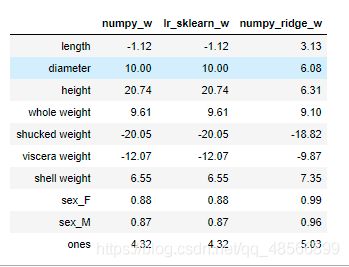
对比numpy和sklearn结果
w_lr=[]
w_lr.extend(lr.coef_)
w_lr.append(lr.intercept_)
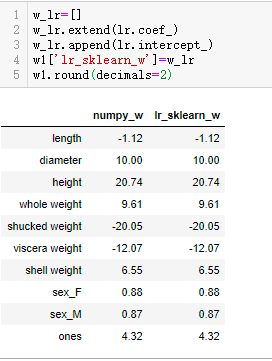
w1['lr_sklearn_w']=w_lr
w1.round(decimals=2)
多重共线性
最小二乘法的参数估计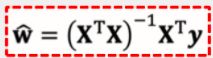
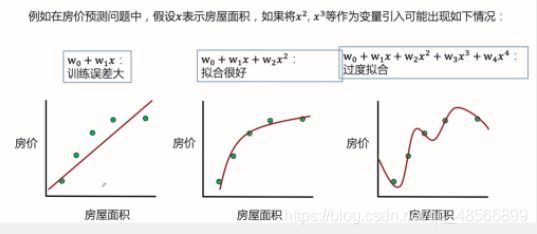
如果变量之间存在较强的共线性,则xtx近似奇异,对参数的估计变得不准确,造成过度拟合现象
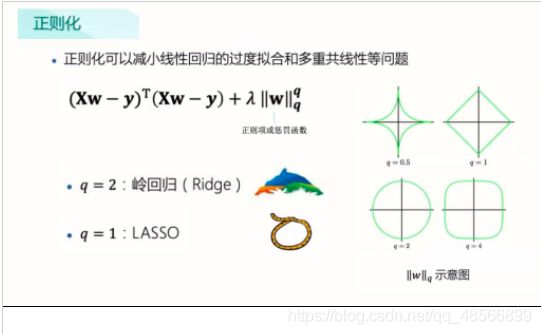
解决办法:正则化,主成分回归,偏最小二乘回归
过度拟合问题:模型变量过多时,可能出现
numpy实现岭回归
def ridge_regression(x,y,ridge_lambda):
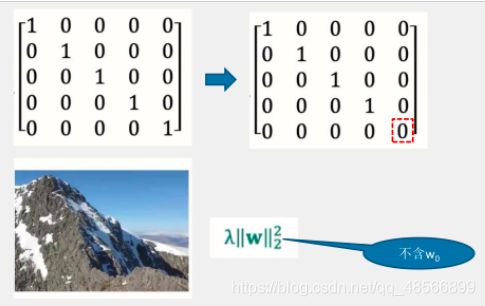
penalty_matrix=np.eye(x.shape[1])
penalty_matrix[x.shape[1]-1][x.shape[1]]=0
w=np.linalg.inv(x.T.dot(x)+ridge_lambda+penalty_matrix).dot(x.T).dot(y)
return w
w2=ridge_regression(x_train,y_train,1.0)
print(w2)
[ 3.13385272 6.07948719 6.30508053 9.10111868 -18.8187455
-9.87193313 7.35094806 0.9876124 0.9553335 5.03494237]
sklearn 岭回归
from sklearn.linear_model import Ridge
ridge=Ridge(alpha=1.0)
ridge.fit(x_train[features_without_ones],y_train)
w_ridge=[]
w_ridge.extend(ridge.coef_)
w_ridge.append(ridge.intercept_)
w1['ridge_sklearn_w']=w_ridge
w1.round(decimals=2)
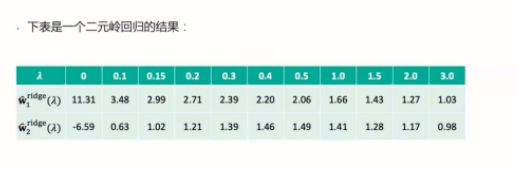
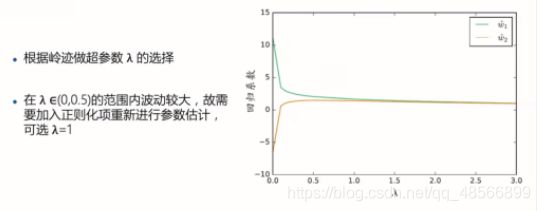
岭迹分析
当不断增大正则化参数lambda,估计参数 w(也称为岭回归系数)在坐标轴上的变化曲线称为岭迹。岭迹波动很大,说明有共线性
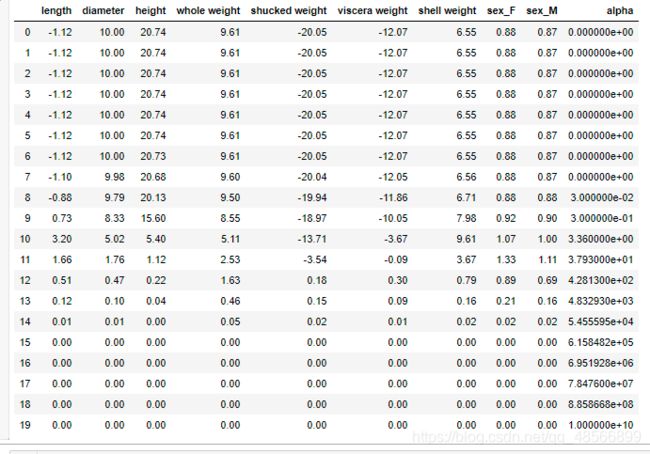
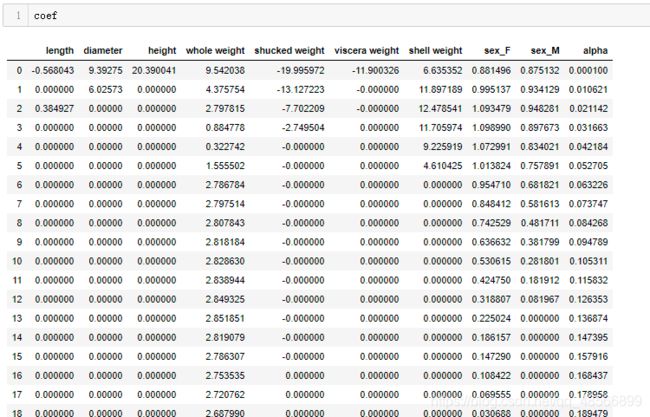
alphas=np.logspace(-10,10,20)
coef=pd.DataFrame()
for alpha in alphas:
ridge_clf=Ridge(alpha=alpha)
ridge_clf.fit(x_train[features_without_ones],y_train)
df=pd.DataFrame([ridge_clf.coef_],columns=x_train[features_without_ones].columns)
df['alpha']=alpha
coef=coef.append(df,ignore_index=True)
coef.round(decimals=2)
import matplotlib.pyplot as plt
%matplotlib inline
#绘图
#显示中文和正负号
plt.rcParams['font.sans-serif']=['SimHei','Time New Romam']
plt.rcParams['axes.unicode_minus']=False
plt.rcParams['figure.dpi']=300
#分辨率
plt.figure(figsize=(9,6))
coef['alpha']=coef['alpha']
for feature in x_train.columns[:-1]:
plt.plot('alpha',feature,data=coef)
ax=plt.gca()
ax.set_xscale('log')
plt.legend(loc='upper right')
plt.xlabel(r'$\alpha$',fontsize=15)
plt.ylabel('系数',fontsize=15)
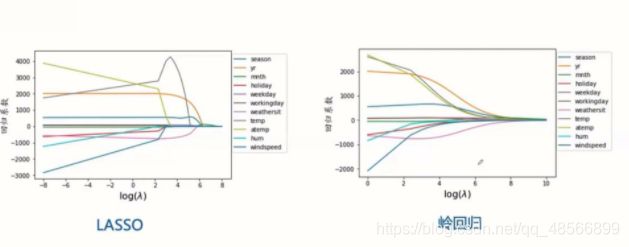
lasso



随着lambda的增大,lasso的特征系数逐个减小为0,可以做特征选择;而岭回归变量系数几乎同时趋近于0
from sklearn.linear_model import Lasso
lasso=Lasso(alpha=0.01)
lasso.fit(x_train[features_without_ones],y_train)
print(lasso.coef_)
print(lasso.intercept_)
[ 0. 6.37435514 0. 4.46703234 -13.44947667
-0. 11.85934842 0.98908791 0.93313403]
6.500338023591298
# lasso 的正则化路径
coef=pd.DataFrame()
for alpha in np.linspace(0.0001,0.2,20):
lasso_clf=Lasso(alpha=alpha)
lasso_clf.fit(x_train[features_without_ones],y_train)
df=pd.DataFrame([lasso_clf.coef_],columns=x_train[features_without_ones].columns)
df['alpha']=alpha
coef=coef.append(df,ignore_index=True)
coef.head()
# 绘图
plt.figure(figsize=(9,6),dpi=600)
for feature in x_train.columns[:-1]:
plt.plot('alpha',feature,data=coef)
plt.legend(loc='upper right')
plt.xlabel(r'$\alpha$',fontsize=15)
plt.ylabel('系数',fontsize=15)
plt.show()
回归的评价指标
mae
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
#mae
y_test_pred_lr=lr.predict(x_test.iloc[:,:-1])
print(round(mean_absolute_error(y_test,y_test_pred_lr),4))
y_test_pred_ridge=ridge.predict(x_test[features_without_ones])
print(round(mean_absolute_error(y_test,y_test_pred_ridge),4))
y_test_pred_lasso=lasso.predict(x_test[features_without_ones])
print(round(mean_absolute_error(y_test,y_test_pred_lasso),4))
1.6016
1.5984
1.6402
mse
#mse
y_test_pred_lr=lr.predict(x_test.iloc[:,:-1])
print(round(mean_squared_error(y_test,y_test_pred_lr),4))
y_test_pred_ridge=ridge.predict(x_test[features_without_ones])
print(round(mean_squared_error(y_test,y_test_pred_ridge),4))
y_test_pred_lasso=lasso.predict(x_test[features_without_ones])
print(round(mean_squared_error(y_test,y_test_pred_lasso),4))
5.3009
4.959
5.1
r2系数
#r2系数
print(round(r2_score(y_test,y_test_pred_lr),4))
print(round(r2_score(y_test,y_test_pred_ridge),4))
print(round(r2_score(y_test,y_test_pred_lasso),4))
残差图
# 残差图
plt.figure(figsize=(9,6),dpi=600)
y_train_pred_ridge=ridge.predict(x_train[features_without_ones])
plt.scatter(y_train_pred_ridge,y_train_pred_ridge-y_train,c='g',alpha=0.6)
plt.scatter(y_test_pred_ridge,y_test_pred_ridge-y_test,c='r',alpha=0.6)
plt.ylabel('Residuals')
plt.xlabel('Predict')