论文笔记:Adaptive Graph Spatial-Temporal Transformer Network for Traffic Flow Forecasting
论文地址
挑战
- 空间图中一个节点对另一个节点的影响可以跨越多个时间步,分别处理空间维度和时间维度数据的方法对直接建模跨时空效应可能是无效的。(在图形建模过程中需要考虑这种跨时空效应)
- 以前的工作通常使用从距离度量或其他地理联系构建的预定图结构,并使用邻接矩阵进行空间建模,但这种地理联系可能不等同于实际的交通关联。(在空间建模方面需要探索真实的空间相关性)
- 即使使用捕捉节点之间真实依赖关系的图,空间相关性也可以在不同的时间步上动态变化,而节点相关性也可能受到时间动态的影响。如何对及时变化的空间相关性进行建模并动态选择相关节点的流量以预测目标流量仍然是一个具有挑战性的问题。
贡献
- 使用局部时空图进行时空建模。具体来说,作者将不同时间步的不同节点视为transformer输入的独立标记,并将注意力范围限制为1跳空间邻居,这保持了复杂性的可扩展性。
- 利用自适应图构造,通过选择目标节点可以参与的节点来探索真正的节点相关性。这将注意力扩展到1跳空间限制之外。
- 设计了一种新的基于transformer的网络架构,用于对时空数据中不同类型的因果效应进行建模。它由基于自注意的ST-attention modules组成,以捕捉动态变化的相关性。
- 在真实的公路交通数据集上进行了大量实验,该模型与基线相比实现了具有竞争力的预测性能。
问题描述
给定一个图 = ( V , E , A ) =(\mathcal{V},\mathcal{E},A) G=(V,E,A)和 T个历史时间步的特征矩阵 X t ∈ R N × D X_t\in\mathbb{R}^{N\times D} Xt∈RN×D,交通预测的目标是学习一个函数 f,它可以预测未来 ′ ' T′个时间步的特征矩阵,即:
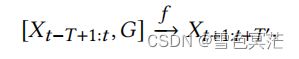
其中 G是固定的,与时域无关; N N N为结点个数; X t − T + 1 : t ∈ R T × N × D X_{t-T+1:t}\in\mathbb{R}^{T\times N\times D} Xt−T+1:t∈RT×N×D, X t + 1 : t + T ′ ∈ R T ′ × N × D X_{t+1:t+T'}\in\mathbb{R}^{T'\times N\times D} Xt+1:t+T′∈RT′×N×D
Multi-Head Self-Attention(这里不过多介绍)
自注意力的思想是通过使用相应的查询键对查询其他token来更新每个令牌自己的值

Local Spatial-Temporal Attention
将具有相同时间步的节点之间的注意力称为空间注意力
将具有相同位置的节点之间的注意力称为时间注意力
使用st-attention来表示具有不同时间步和位置的节点对的注意力。
构建时空图transformer可以考虑不同类型的注意。
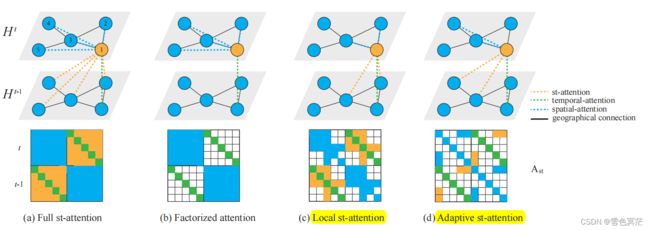
上半部分表示在两个时间步上的相同图(具有自连接),而节点1在时间t上希望使用注意力机制基于其他可能相关的节点更新其自身的表示。下半部分表示相应的时空注意力矩阵。带有颜色的项表示对应的两个节点(由行和列索引确定)将相互关注,不同的颜色对应于不同类型的attentions。
Full st-attention
是融合时空注意最直接的方法,对时空图中的每一对节点进行注意,并将每个节点表示 h , ∈ R ℎ_{,}\in \mathbb{R}^ ht,i∈RD作为一个token。这样 h , ℎ_{,} ht,i可以参与来自输入的所有tokens,输入节点的特征矩阵 = [ h , ] ∈ R T × N × D =[ℎ_{,}]_{}\in \mathbb{R}^{T\times N\times D} H=[ht,i]ti∈RT×N×D。
可以捕获两个在空间和时间域上可能彼此远离的节点的注意力。
时间复杂度为 O ( T 2 N 2 ) O(T^2N^2) O(T2N2)
Factorized attention
将st-attention分解到空间维度和时间维度,然后逐个计算注意力:在空间上,每个节点只能水平参与同一时间步的节点;而在时间上,每个节点只能垂直参与同一位置的节点。
该方法没有直接考虑动态的st-attention,通过空间注意力和时间注意力相结合获得st-attention。
时间复杂度为 O ( T 2 + N 2 ) O(T^2+N^2) O(T2+N2),
Local st-attention
利用空间邻接性,通过将st-attention保持在空间1跳邻域内来降低注意力的复杂性:将每个节点的范围限制在其地理邻居上,并计算具有这些地理位置的所有节点的注意力。
从矩阵的角度,相当于对full st-attention矩阵使用了适当的st-attention mask。具体来说,可将输入特征矩阵flatten为 ∈ R T N × D \in \mathbb{R}^{TN\times D} H∈RTN×D,st-attention mask用 A s t ∈ R T N × T N A_{st}\in \mathbb{R}^{TN\times TN} Ast∈RTN×TN表示,局部多头自注意(L-MSA)公式如下:
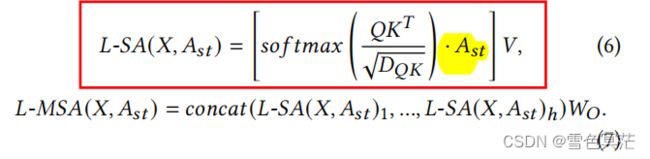
时间复杂度为 O ( 2 ) O(^2) O(ET2), E表示空间图中的边的总数,对稀疏图是可扩展的。
注:限制对空间邻域的注意力是合理的,因为随着层数的增加,可以捕捉到远程的空间相关性,而远程的空间注意力通常较弱。我们沿着时间维度保持充分的注意力,因为 T通常比不同位置 N的数量要小
Adaptive st-attention
地理邻接可能不能反映节点之间的真正依赖关系,为探索真实的空间相关性并提高Local st-attention的性能,作者引入了可学习的自适应图 G a p t G_{apt} Gapt 。该图可以帮助目标节点选择相关节点进行关注,其邻接矩阵 _{} Aapt不需要任何先验知识,即可进行端到端学习。
_{} Aapt的计算公式如下:

其中, 1 , 2 ∈ R N × c _1,_2\in \mathbb{R}^{N\times c} U1,U2∈RN×c为随机初始化的可学习的节点嵌入; b b b为使用Gumbel-sigmoid技巧基于 _{} Aapt的每项(entry)计算出的二进制掩码; ∈ R N × N _{}\in\mathbb{R}^{N\times N} Aapt∈RN×N,维度与图结构 G G G的邻接矩阵 A A A相同
注:第一个公式(无b)计算出的邻接矩阵将得到一个完整的图(每对节点都是连接的),对其应用局部注意将等同于full st-attention方法。第二公式中使用的是元素乘法
影响
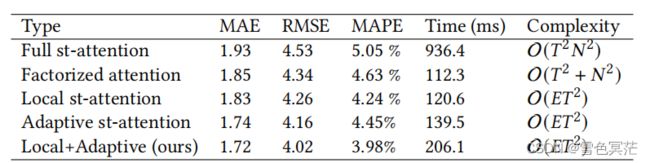
注:"Times"指标是指具有相同输入batch size的平均正向通过时间。
- Full st-attention很难被训练,而且可能表现得最糟糕;
- Factorized attention比Full st-attention的表现好并且运行地更快;
- Local st-attention和Adaptive st-attention与Factorized attention相比具有相当的运行时间。
- Adaptive st-attention的表现优于前三种方法,因为它可以探索真正的节点交互;论文采用的Local + Adaptive st-attention在可接受的运行时间下获得了最佳的预测性能。
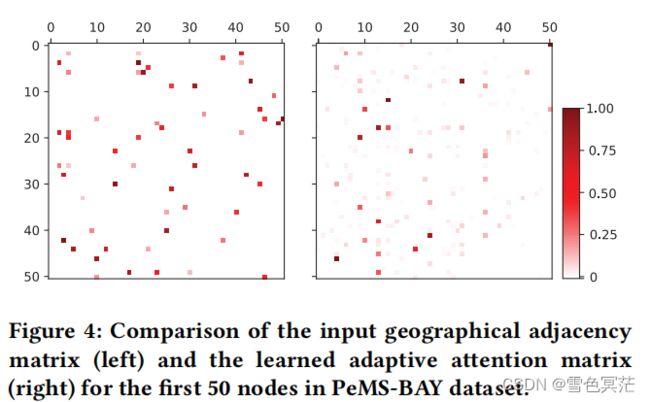
此外,作者利用PEMS-BAY数据集进一步研究了学习到的自适应邻接矩阵。与原始的地理邻接矩阵相比,因为应用了基于相关值的mask,学习到的自适应邻接显示出了节点间更多的稀疏相关性。此外,自适应邻接矩阵揭示了许多在输入邻接图中没有显示出来的相关性,这意味着地理相关性可能无法描述真实的节点依赖性。
ASTTN的框架
ASTTN的框架由输入层、时空嵌入层、具有残差连接的堆叠st-attention块和输出层组成。该模型的输入包括一个特征矩阵 X ∈ R T × N × D i n X\in\mathbb{R}^{T\times N\times D_{in}} X∈RT×N×Din,一个底层图结构 G和时空嵌入STE
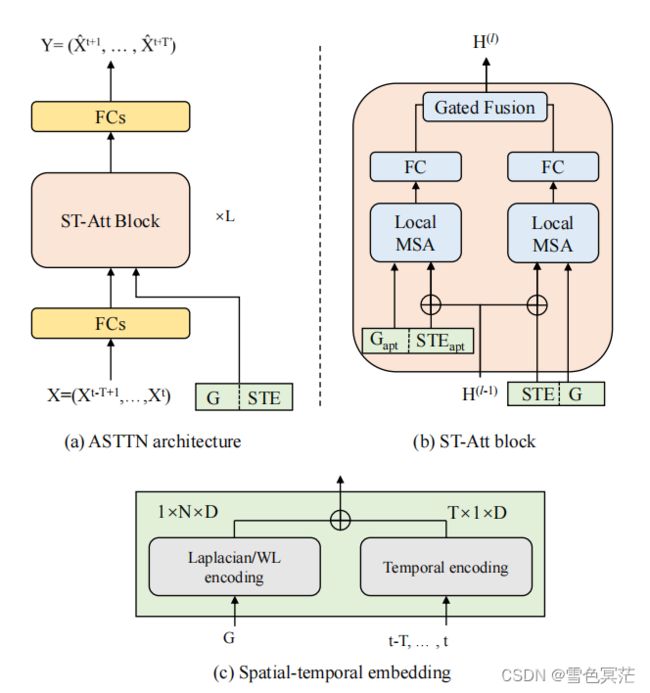
输入层和输出层是具有ReLU激活的全连接网络。输入层用于将输入节点特征映射到更高维度 D D D;输出层用于将时间维度从历史时间步长 T T T映射到未来时间维度 T ′ T^′ T′。
时空嵌入层利用图结构对结构信息进行编码。时空嵌入是通过张量广播将空间和时间嵌入相加而获得的,空间和时间嵌入分别计算得到,用linear层投影到同一维度。
st-attention块的输入和输出分别表示为 ( − 1 ) ^{(−1)} H(l−1)和 ( ) ∈ R T × N × D ^{()}\in\mathbb{R}^{T\times N\times D} H(l)∈RT×N×D,它们具有相同的维度 D,以便于残差连接。每个st-attention块对输入图和可训练自适应图执行两个局部多头部自注意力(Local MSA),并融合结果获得输出。
Spatial-Temporal Embedding
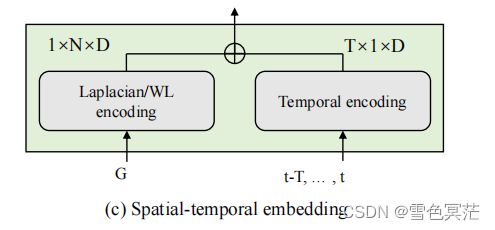
空间嵌入(位置嵌入):使用图结构的拉普拉斯位置编码向每个输入token添加positional encoding,确保唯一的表示和保存距离信息。
-
按以下公式计算输入图的拉普拉斯特征向量,其中, A为邻接矩阵, D D D为图的度矩阵, Λ \Lambda Λ为特征值矩阵, U为特征向量矩阵;
L = T − D − 1 / 2 A D − 1 / 2 = U T Λ U L=T-D^{-1/2}AD^{-1/2}=U^T\Lambda U L=T−D−1/2AD−1/2=UTΛU -
用每个节点的 k个最小非平凡特征向量作为其位置嵌入;
-
将位置嵌入输入到FC(全连接)层中,以保持与输入 X相同的维度。
时间嵌入:考虑了交通的周期性,作者遵循GMAN中的方式,使用one-hot coding将每个时间步的day-of-week和time-of-day进行编码,然后concatenate为时间编码,最后同样将其输入到FC层。
st-embedding(STE):由位置嵌入和时间嵌入相加得到,用于描述图结构中的一个节点在不同时间步中的唯一位置。
ST-Attention Block
ST-attention block由两个并行的局部多头注意力模块组成,对输入的流量矩阵 ( − 1 ) ∈ R T × N × D ^{(−1)}\in\mathbb{R}^{T\times N\times D} H(l−1)∈RT×N×D执行局部时空注意力。与以往使用分离模块进行时空域建模的工作相比,ST-attention模块能同时更新时空域的节点嵌入。
这两个Local MSA模块是基于两组不同的图和st-embedding的。第一个是原始路线图 G,其邻接矩阵 ∈ R N × N \in\mathbb{R}^{N\times N} A∈RN×N由原始的地理联系决定。第二个是自适应图 _{} Gapt,其邻接矩阵为 _{} Aapt。
- 分别基于 G和 _{} Gapt计算两种时空嵌入类型的STE和STEapt,然后加到输入 ( − 1 ) ^{(−1)} H(l−1)中。
- Local MSA模块按照对应公式计算局部时空注意力,其中输入的特征矩阵是flatten后的输入 ( − 1 ) ^{(−1)} H(l−1),输入的st-attention mask由 A或 _{} Aapt构造。
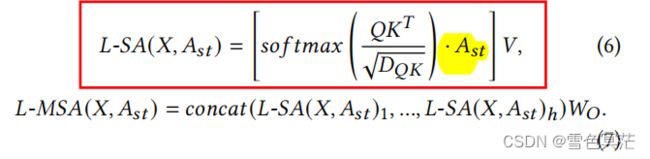
- 最后,两个并行Local MSA模块的输出使用门控融合机制融合在一起。
但在具体实现中,作者并没有明确地构造特征矩阵和st-attention mask
实际做法:利用输入图的稀疏性,作者使用了DGL包,它可以执行快速和内存高效的消息传递原语来训练图神经网络。为有效地计算st-attention,只使用DGL构建空间图以避免大量的内存使用,并计算 , , ∈ R T × N × D ,,\in\mathbb{R}^{T\times N\times D} Q,K,V∈RT×N×D ;接下来固定 Q矩阵,同时沿第一个时间维滚动 , , K,V矩阵为1;然后使用DGL进行消息传递,将这个 , , ,, Q,K,V对分配给每个节点,用下式计算注意力。
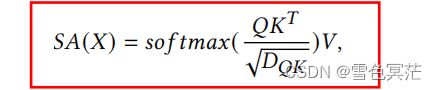
通过这种方式,实际上是在计算两个相邻时间步长之间的st-attention(图2中的橙色虚线)。将这个滚动过程重复 T次,总的结果等同于计算 L − S A ( X , A s t ) L-SA(X,A_{st}) L−SA(X,Ast).
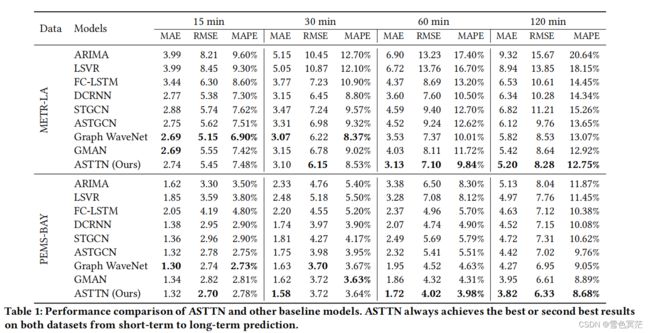
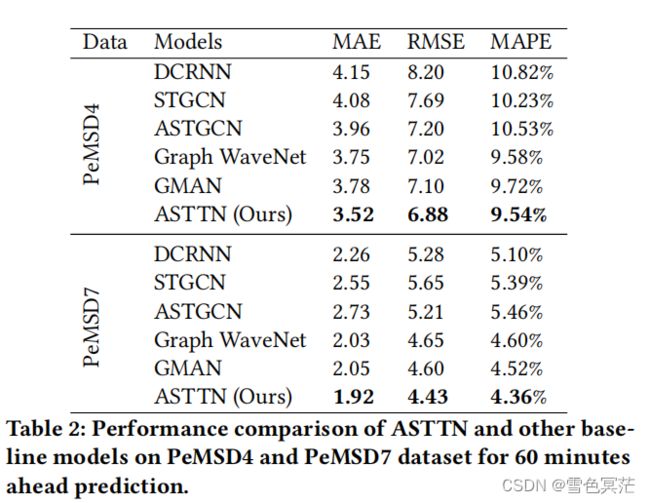
实验结果
- 表明了深度学习模型的威力,以及将图结构纳入时间预测的重要性
- Graph WaveNet和ASTTN在图结构建模方面优于图模型DCRNN和STGCN,表明需要探索真正的空间依赖性来提高模型的性能。
- GMAN和ASTTN也优于传统的图深度学习模型,表明了捕获动态时空相关性的重要性。
- 与基准测试相比,ASTTN实现了最先进的预测性能,不管是在短期预测还是长期预测中都取得了最优或第二优的结果,并且在长期水平预测中其优势更为明显。短期预测的表现相对较低,可能是因为st-attention效应相对较弱,而空间注意可以发挥更重要的作用,因为时间维度的变化相对较小。
消融实验
为研究ASTTN模型中每个组件的影响,作者通过去除时空节点嵌入(ASTTN-NE)、门控融合(ASTTN-NF)和自适应 local-MSA模块(ASTTN-NA)来评估模型变体的性能。ASTTN始终优于其变体,表明了以上三个部分在捕获复杂的时空依赖性方面的重要性。

总结
- 在该论文中中,作者提出了一种新的模型,称为ASTNN,用于交通预测的图结构时空建模。ASTNN是由堆叠的ST-Attention Block构建的,用于同时建模空间和时间相关性。
- 作者使用局部多头自注意(L-MSA)来有效地计算时空图上的关注。
- 此外,为了探索真实的空间相关性并提高局部时空注意力的性能,还引入了可学习自适应图,该图可以帮助目标节点选择相关节点进行关注。
- 作者比较了不同类型的时空注意力的效果,并显示了局部时空注意力的有效性。
- 对四个交通数据集的综合实证研究表明,与最先进的基线相比,ASTNN具有优越的性能。
- 消融研究和自适应邻接矩阵的可视化显示了我们模型的每个组件的影响。