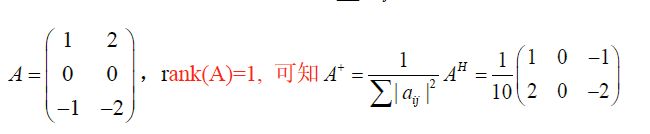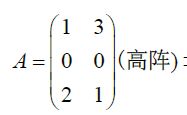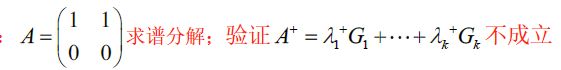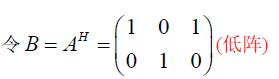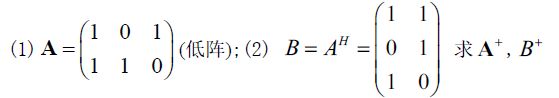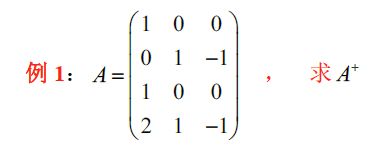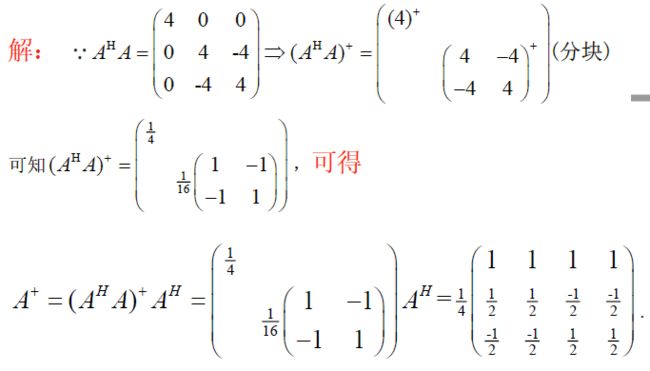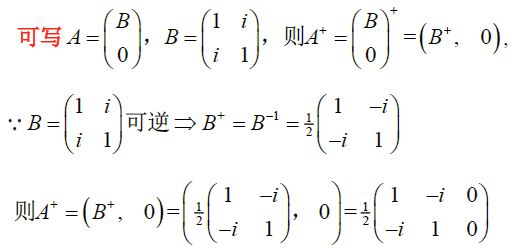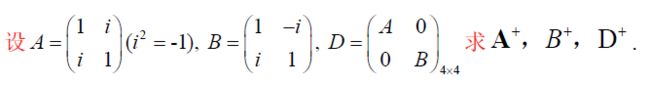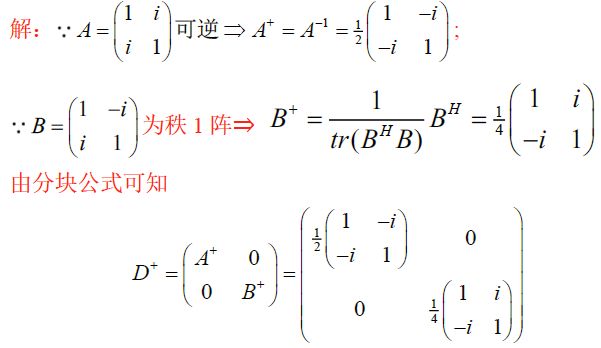【矩阵论】4. 矩阵运算——广义逆——广义逆的计算
4.3.2 A + A^+ A+ 计算
a. 秩1公式
若 A = ( a i j ) m × n , r ( A ) = 1 , 则 A + = 1 ∑ ∣ a i j ∣ 2 A H = 1 t r ( A H A ) A H \begin{matrix} 若A=(a_{ij})_{m\times n},r(A)=1,则A^+=\frac{1}{\sum \vert a_{ij}\vert^2}A^H=\frac{1}{tr(A^HA)}A^H \end{matrix} 若A=(aij)m×n,r(A)=1,则A+=∑∣aij∣21AH=tr(AHA)1AH
A H A A^HA AHA 的相关结论:
- t r ( A H A ) = t ( A A H ) = ∑ ∣ a i j ∣ 2 = ∥ A ∥ F 2 tr(A^HA)=t(AA^H)=\sum\vert a_{ij}\vert^2=\Vert A \Vert_F^2 tr(AHA)=t(AAH)=∑∣aij∣2=∥A∥F2
- r ( A H A ) = r ( A A H ) = r ( A ) r(A^HA)=r(AA^H)=r(A) r(AHA)=r(AAH)=r(A)
- A H A , A A H A^HA,AA^H AHA,AAH 为半正定阵
证明:
由 于 r ( A ) = 1 , 则 A H A 优 相 似 与 对 角 阵 D = ( λ 1 0 ⋱ 0 ) , 其 中 λ 1 为 正 奇 值 ⇒ t r ( A H A ) = t r ( A A H ) = λ 1 = ∑ ∣ a i j ∣ 2 , 则 A 的 正 S V D 为 A = P Δ Q H = P ( λ 1 ) Q H , 其 中 P H P = Q H Q = I A H = Q Δ P H = Q ( λ 1 ) P H , A + = Q Δ − 1 P H = Q ( 1 λ 1 ) P H ⇒ A + = 1 ( λ 1 ) 2 Q ( λ 1 ) P H = 1 ( λ 1 ) 2 Q Δ P H = 1 ( λ 1 ) 2 A H = 1 t r ( A H A ) A H = 1 ∑ ∣ a i j ∣ 2 A H \begin{aligned} &由于r(A)=1,则A^HA优相似与对角阵D=\left( \begin{matrix} \lambda_1&&&\\&0&\\&&\ddots&\\&&&0 \end{matrix} \right),其中\sqrt{\lambda_1} 为正奇值\Rightarrow\\ &tr(A^HA)=tr(AA^H)=\lambda_1=\sum\vert a_{ij}\vert^2,则A的正SVD为A=P\Delta Q^H=P\left(\sqrt{\lambda_1}\right)Q^H,\\ &其中P^HP=Q^HQ=I\\ &A^H=Q\Delta P^H=Q(\sqrt{\lambda_1})P^H,A^+=Q\Delta^{-1}P^H=Q(\frac{1}{\sqrt{\lambda_1}})P^H\\ &\Rightarrow A^+=\frac{1} {(\sqrt{\lambda_1})^2}Q(\sqrt{\lambda_1})P^H=\frac{1}{(\sqrt{\lambda_1})^2}Q\Delta P^H=\frac{1}{(\sqrt{\lambda_1})^2}A^H=\frac{1}{tr(A^HA)}A^H=\frac{1}{\sum \vert a_{ij}\vert^2}A^H\\ \end{aligned} 由于r(A)=1,则AHA优相似与对角阵D=⎝⎜⎜⎛λ10⋱0⎠⎟⎟⎞,其中λ1为正奇值⇒tr(AHA)=tr(AAH)=λ1=∑∣aij∣2,则A的正SVD为A=PΔQH=P(λ1)QH,其中PHP=QHQ=IAH=QΔPH=Q(λ1)PH,A+=QΔ−1PH=Q(λ11)PH⇒A+=(λ1)21Q(λ1)PH=(λ1)21QΔPH=(λ1)21AH=tr(AHA)1AH=∑∣aij∣21AH
eg:
b. 正奇公式(第一公式)
若 A = A m × n 有 正 S V D , A = P Δ Q H , Δ = ( s 1 ⋱ s r ) > 0 , 其 中 P , Q 为 半 U 阵 , P H P = I r = Q H Q 则 有 公 式 A + = Q Δ − 1 P H , 其 中 Δ − 1 = Δ + \begin{aligned} &若A=A_{m\times n} 有正SVD,A=P\Delta Q^H,\Delta=\left( \begin{matrix} s_1&&\\&\ddots&\\&&s_r \end{matrix} \right)>0,\\ &其中P,Q为半U阵,P^HP=I_r=Q^HQ\\ &则有公式A^+=Q\Delta^{-1}P^H,其中 \Delta^{-1}=\Delta^{+} \end{aligned} 若A=Am×n有正SVD,A=PΔQH,Δ=⎝⎛s1⋱sr⎠⎞>0,其中P,Q为半U阵,PHP=Ir=QHQ则有公式A+=QΔ−1PH,其中Δ−1=Δ+
由 A + A^+ A+ 的正奇公式,可证 逆的H穿脱公式 ( A H ) + = ( A + ) H (A^H)^+=(A^+)^H (AH)+=(A+)H
- A + A^+ A+ 的正奇值为 { s 1 − 1 , s 2 − 1 , ⋯ , s r − 1 } \{s_1^{-1},s_2^{-1},\cdots,s_r^{-1}\} {s1−1,s2−1,⋯,sr−1} ,且有公式 ∥ A + ∥ F = s 1 − 2 , ⋯ , s r − 2 \Vert A^+\Vert_F=\sqrt{s_1^{-2},\cdots,s_r^{-2}} ∥A+∥F=s1−2,⋯,sr−2 , ∥ A + ∥ 2 = s r − 1 \Vert A^+\Vert_2=s_r^{-1} ∥A+∥2=sr−1
证明:
A = P Δ Q H ⇒ A H = Q Δ P H 为 A H 的 正 S V D A + = Q Δ − 1 P H , ( A H ) + = P Δ − 1 Q H ⇒ ( A + ) H = P Δ − 1 Q H = ( A H ) + \begin{aligned} &A=P\Delta Q^H\Rightarrow A^H=Q\Delta P^H为A^H的正SVD\\ &A^+=Q\Delta^{-1}P^H,(A^H)^+=P\Delta^{-1}Q^H\Rightarrow (A^+)^H=P\Delta^{-1}Q^H=(A^H)^+ \end{aligned} A=PΔQH⇒AH=QΔPH为AH的正SVDA+=QΔ−1PH,(AH)+=PΔ−1QH⇒(A+)H=PΔ−1QH=(AH)+
eg

( 1 ) 求 正 奇 值 , A H A = ( 1 0 2 0 1 0 ) ( 1 0 0 1 2 0 ) = ( 5 0 0 1 ) , λ ( A ) = { 5 , 1 } , 正 奇 值 为 5 , 1 , 令 Δ = ( 5 0 0 1 ) ( 2 ) S V D , Q = ( q 1 , q 2 ) = ( 1 0 0 1 ) , P = ( A q 1 ∣ A q 1 ∣ , A q 2 ∣ A q 2 ∣ ) = ( 1 5 0 0 1 2 5 0 ) , A = P Δ Q H = ( 1 5 0 0 1 2 5 0 ) ( 5 0 0 1 ) ( 1 0 0 1 ) H ( 3 ) A + = Q Δ − 1 P H = ( 1 0 0 1 ) 1 5 ( 1 0 0 5 ) ( 1 5 0 2 5 0 1 0 ) = ( 1 5 0 0 1 ) ( 1 5 0 2 5 0 1 0 ) = ( 1 5 0 2 5 0 1 0 ) ( 4 ) ∵ B = A H , 则 B + = ( A H ) + = ( A + ) H = ( 1 5 0 0 1 2 5 0 ) \begin{aligned} &(1)求正奇值,A^HA=\left( \begin{matrix} 1&0&2\\0&1&0 \end{matrix} \right)\left( \begin{matrix} 1&0\\0&1\\2&0 \end{matrix} \right)=\left( \begin{matrix} 5&0\\0&1 \end{matrix} \right),\lambda(A)=\{5,1\},正奇值为\sqrt{5},1,令\Delta=\left( \begin{matrix} \sqrt{5} & 0\\0&1 \end{matrix} \right)\\ &(2)SVD,Q=(q_1,q_2)=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right),P=\left( \begin{matrix} \frac{Aq_1}{\vert Aq_1\vert},\frac{Aq_2}{\vert Aq_2\vert} \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{5}}&0\\0&1\\\frac{2}{\sqrt{5}}&0\\ \end{matrix} \right),A=P\Delta Q^H=\left( \begin{matrix} \frac{1}{\sqrt{5}}&0\\0&1\\\frac{2}{\sqrt{5}}&0\\ \end{matrix} \right)\left( \begin{matrix} \sqrt{5} & 0\\0&1 \end{matrix} \right)\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)^H\\ &(3)A^+=Q\Delta^{-1}P^H=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)\frac{1}{\sqrt{5}}\left( \begin{matrix} 1&0\\0&\sqrt{5} \end{matrix} \right)\left( \begin{matrix} \frac{1}{\sqrt{5}}&0&\frac{2}{\sqrt{5}}\\0&1&0\\ \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{5}}&0\\0&1 \end{matrix} \right)\left( \begin{matrix} \frac{1}{\sqrt{5}}&0&\frac{2}{\sqrt{5}}\\0&1&0\\ \end{matrix} \right)=\left( \begin{matrix} \frac{1}{5}&0&\frac{2}{5}\\ 0&1&0 \end{matrix} \right)\\ &(4)\because B=A^H,则B^+=(A^H)^+=(A^+)^H=\left( \begin{matrix} \frac{1}{5}&0\\0&1\\\frac{2}{5}&0 \end{matrix} \right) \end{aligned} (1)求正奇值,AHA=(100120)⎝⎛102010⎠⎞=(5001),λ(A)={5,1},正奇值为5,1,令Δ=(5001)(2)SVD,Q=(q1,q2)=(1001),P=(∣Aq1∣Aq1,∣Aq2∣Aq2)=⎝⎛51052010⎠⎞,A=PΔQH=⎝⎛51052010⎠⎞(5001)(1001)H(3)A+=QΔ−1PH=(1001)51(1005)(51001520)=(51001)(51001520)=(51001520)(4)∵B=AH,则B+=(AH)+=(A+)H=⎝⎛51052010⎠⎞

A H A = ( 2 1 1 2 ) , λ ( A H A ) = { 3 , 1 } , 正 奇 值 S + = { 3 , 1 } , 故 A H A 优 相 似 与 Δ = ( 3 0 0 1 ) , λ 1 = 3 的 特 根 q 1 = ( 1 1 ) , λ 2 = 1 的 特 根 为 q 2 = ( 1 − 1 ) , Q = ( q 1 , q 2 ) = ( 1 2 1 2 1 2 − 1 2 ) , P = ( A q 1 ∣ A q 1 ∣ , A q 2 ∣ A q 2 ∣ ) = ( 1 6 ( 1 1 2 ) , 1 2 ( 1 − 1 0 ) ) = ( 1 6 1 2 1 6 − 1 2 2 6 0 ) A = P Δ Q H = ( 1 6 1 2 1 6 − 1 2 2 6 0 ) ( 3 0 0 1 ) ( 1 2 1 2 1 2 − 1 2 ) A + = Q Δ − 1 P H = ( 1 2 1 2 1 2 − 1 2 ) ( 1 3 0 0 1 ) ( 1 6 1 6 2 6 1 2 − 1 2 0 ) = 1 6 = ( 4 − 2 2 − 2 4 2 ) \begin{aligned} &A^HA=\left( \begin{matrix} 2&1\\1&2 \end{matrix} \right),\lambda(A^HA)=\{3,1\},正奇值S^+=\{\sqrt{3},1\},故A^HA优相似与\Delta=\left( \begin{matrix} \sqrt{3}&0\\0&1 \end{matrix} \right),\\ &\lambda_1=3的特根q_1=\left( \begin{matrix} 1\\1 \end{matrix} \right),\lambda_2=1的特根为q_2=\left( \begin{matrix} 1\\-1 \end{matrix} \right),\\ &Q=(q_1,q_2)=\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{matrix} \right),P=\left(\frac{Aq_1}{\vert Aq_1 \vert},\frac{Aq_2}{\vert Aq_2 \vert}\right)=\left( \begin{matrix} \frac{1}{\sqrt{6}}\left( \begin{matrix} 1\\1\\2 \end{matrix} \right),\frac{1}{\sqrt{2}}\left( \begin{matrix} 1\\-1\\0 \end{matrix} \right) \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{6}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}&-\frac{1}{\sqrt{2}}\\ \frac{2}{\sqrt{6}}&0\\ \end{matrix} \right)\\ &A=P\Delta Q^H=\left( \begin{matrix} \frac{1}{\sqrt{6}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}&-\frac{1}{\sqrt{2}}\\ \frac{2}{\sqrt{6}}&0\\ \end{matrix} \right)\left( \begin{matrix} \sqrt{3}&0\\0&1 \end{matrix} \right)\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{matrix} \right)\\ &A^+=Q\Delta^{-1}P^H=\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{matrix} \right)\left( \begin{matrix} \frac{1}{\sqrt{3}}&0\\0&1 \end{matrix} \right)\left( \begin{matrix} \frac{1}{\sqrt{6}}&\frac{1}{\sqrt{6}}&\frac{2}{\sqrt{6}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0\\ \end{matrix} \right)=\frac{1}{6}=\left( \begin{matrix} 4&-2&2\\-2&4&2 \end{matrix} \right) \end{aligned} AHA=(2112),λ(AHA)={3,1},正奇值S+={3,1},故AHA优相似与Δ=(3001),λ1=3的特根q1=(11),λ2=1的特根为q2=(1−1),Q=(q1,q2)=(212121−21),P=(∣Aq1∣Aq1,∣Aq2∣Aq2)=⎝⎛61⎝⎛112⎠⎞,21⎝⎛1−10⎠⎞⎠⎞=⎝⎜⎛61616221−210⎠⎟⎞A=PΔQH=⎝⎜⎛61616221−210⎠⎟⎞(3001)(212121−21)A+=QΔ−1PH=(212121−21)(31001)(612161−21620)=61=(4−2−2422)
c. 优分解公式
设 P , Q 为 优 阵 , 则 ( P D Q ) + = Q H D + P H = Q H D P H \begin{aligned} &设P,Q为优阵,则 (PDQ)^+=Q^HD^+P^H=Q^HDP^H \end{aligned} 设P,Q为优阵,则(PDQ)+=QHD+PH=QHDPH
- 引理:若 D = ( λ 1 ⋱ λ n ) D=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right) D=⎝⎛λ1⋱λn⎠⎞ 为对角阵,则 D + D = D D + D^+D=DD^+ D+D=DD+ ,且 ( D + ) k = ( D k ) + (D^+)^k=(D^k)^+ (D+)k=(Dk)+ ,(k=1,2,…)
d. QR分解公式
设 A = A m × p 为 高 阵 , 且 有 Q R 分 解 , A = Q R , Q 为 列 U 阵 , R = R p × p , 则 A + = R − 1 Q H \begin{aligned} &设A=A_{m\times p}为高阵,且有QR分解,A=QR,Q为列U阵,R=R_{p\times p},则A^+=R^{-1}Q^H \end{aligned} 设A=Am×p为高阵,且有QR分解,A=QR,Q为列U阵,R=Rp×p,则A+=R−1QH
eg
( 1 ) 求 A 的 Q R 分 解 , 令 β 1 = ( 1 0 2 ) , β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 = ( 2 0 − 1 ) , Q = 1 5 ( 1 2 0 0 2 − 1 ) R = Q H A = 5 ( 1 1 0 1 ) ⇒ A = Q R = 1 5 ( 1 2 0 0 2 − 1 ) 5 ( 1 1 0 1 ) ( 2 ) A + = ( Q R ) + = R + Q + = R − 1 Q H = 1 5 ( 1 − 1 0 1 ) 1 5 ( 1 0 2 2 0 − 1 ) = 1 5 ( − 1 0 3 2 0 − 1 ) \begin{aligned} &(1)求A的QR分解,令\beta_1=\left( \begin{matrix} 1\\0\\2 \end{matrix} \right),\beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{(\beta_1,\beta_1)}\beta_1=\left( \begin{matrix} 2\\0\\-1 \end{matrix} \right),Q=\frac{1}{\sqrt{5}}\left( \begin{matrix} 1&2\\0&0\\2&-1 \end{matrix} \right)\\ &\quad R=Q^HA=\sqrt{5}\left( \begin{matrix} 1&1\\0&1 \end{matrix} \right)\Rightarrow A=QR=\frac{1}{\sqrt{5}}\left( \begin{matrix} 1&2\\0&0\\2&-1 \end{matrix} \right)\sqrt{5}\left( \begin{matrix} 1&1\\0&1 \end{matrix} \right)\\ &(2)A^+=(QR)^+=R^+Q^+=R^{-1}Q^H=\frac{1}{\sqrt{5}}\left( \begin{matrix} 1&-1\\0&1 \end{matrix} \right)\frac{1}{\sqrt{5}}\left( \begin{matrix} 1&0&2\\2&0&-1 \end{matrix} \right)=\frac{1}{5}\left( \begin{matrix} -1&0&3\\ 2&0&-1 \end{matrix} \right) \end{aligned} (1)求A的QR分解,令β1=⎝⎛102⎠⎞,β2=α2−(β1,β1)(α2,β1)β1=⎝⎛20−1⎠⎞,Q=51⎝⎛10220−1⎠⎞R=QHA=5(1011)⇒A=QR=51⎝⎛10220−1⎠⎞5(1011)(2)A+=(QR)+=R+Q+=R−1QH=51(10−11)51(12002−1)=51(−12003−1)
e. 单阵谱分解
若A为单阵不可逆,则不能用谱分解方式求逆
t r ( A ) = 1 , 故 A + = 1 2 A H = 1 2 ( 1 0 1 0 ) A 的 特 征 多 项 式 为 ∣ A − λ I ∣ = λ ( 1 − λ ) ⇒ λ ( A ) = { 1 , 0 } , G 1 = A − λ 2 I λ 1 − λ 2 = ( 1 1 0 0 ) A 有 谱 分 解 A = G 1 , A + ≠ A , 故 对 于 不 可 逆 的 单 阵 , A + ≠ λ 1 − 1 G 1 + ⋯ + λ k − 1 G k \begin{aligned} &tr(A)=1,故A^+=\frac{1}{2}A^H=\frac{1}{2}\left( \begin{matrix} 1&0\\1&0 \end{matrix} \right)\\ &A的特征多项式为 \vert A-\lambda I\vert=\lambda(1-\lambda)\Rightarrow \lambda(A)=\{1,0\},G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\left( \begin{matrix} 1&1\\0&0 \end{matrix} \right)\\ &A有谱分解A=G_1,A^+\neq A,故对于不可逆的单阵,A^+\neq \lambda_1^{-1}G_1+\cdots+\lambda_k^{-1}G_k \end{aligned} tr(A)=1,故A+=21AH=21(1100)A的特征多项式为∣A−λI∣=λ(1−λ)⇒λ(A)={1,0},G1=λ1−λ2A−λ2I=(1010)A有谱分解A=G1,A+=A,故对于不可逆的单阵,A+=λ1−1G1+⋯+λk−1Gk
若A为单阵且可逆,则有谱分解 A = λ 1 G 1 + ⋯ + λ k G k A=\lambda_1G_1+\cdots+\lambda_kG_k A=λ1G1+⋯+λkGk 且 A + = λ 1 − 1 G 1 + ⋯ + λ k − 1 G k A^+=\lambda_1^{-1}G_1+\cdots+\lambda_k^{-1}G_k A+=λ1−1G1+⋯+λk−1Gk
A 为 行 和 阵 , λ ( A ) = { 4 , 1 } , G 1 = A − λ 2 I λ 1 − λ 2 = 1 3 ( 1 2 1 2 ) , G 2 = 1 3 ( 2 − 2 − 1 1 ) , A = 4 G 1 + G 2 r ( A ) = 2 , 则 A 可 逆 , 故 ⇒ A + = A − 1 = 1 3 G 1 + G 2 = 1 4 ( 3 − 2 − 1 2 ) \begin{aligned} &A为行和阵,\lambda(A)=\{4,1\},G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{3}\left( \begin{matrix} 1&2\\1&2 \end{matrix} \right),G_2=\frac{1}{3}\left( \begin{matrix} 2&-2\\-1&1 \end{matrix} \right),A=4G_1+G_2\\ &r(A)=2,则A可逆,故\Rightarrow A^+=A^{-1}=\frac{1}{3}G_1+G_2=\frac{1}{4}\left( \begin{matrix} 3&-2\\-1&2 \end{matrix} \right) \end{aligned} A为行和阵,λ(A)={4,1},G1=λ1−λ2A−λ2I=31(1122),G2=31(2−1−21),A=4G1+G2r(A)=2,则A可逆,故⇒A+=A−1=31G1+G2=41(3−1−22)
正规阵谱分解
若 A 为 正 规 阵 , 且 有 谱 分 解 : A = λ 1 G 1 + ⋯ + λ k G k , 则 有 A + = λ 1 + G 1 + λ 2 + G 2 + ⋯ + λ k + G k \begin{aligned} &若A为正规阵,且有谱分解:A=\lambda_1G_1+\cdots+\lambda_kG_k,则有 A^+=\lambda_1^+G_1+\lambda_2^+G_2+\cdots+\lambda_k^+G_k \end{aligned} 若A为正规阵,且有谱分解:A=λ1G1+⋯+λkGk,则有A+=λ1+G1+λ2+G2+⋯+λk+Gk
eg
( 1 ) 求 A 的 谱 分 解 : A 有 特 征 多 项 式 ∣ A − λ I ∣ = ∣ 2 − λ 1 − i 1 + i 1 − λ ∣ = ( 2 − λ ) ( 1 − λ ) − 2 = λ ( λ − 3 ) ⇒ λ ( A ) = { 3 , 0 } G 1 = A − λ 2 I λ 1 − λ 2 = 1 3 ( 2 1 − i 1 + i 1 ) , G 2 = I − G 1 = 1 3 ( 1 1 − i − 1 − i 2 ) 可 得 谱 分 解 A = 3 G 1 + 0 G 2 ( 2 ) A + = 3 + G 1 = 1 3 G 1 = 1 9 ( 2 1 − i 1 + i 1 ) 验 证 : ( 1 − i ) r 2 = r 1 , 即 A 为 秩 1 公 式 , 故 有 A + = 1 ∑ ∣ a i j ∣ 2 ( 2 1 + i 1 − i 1 ) = 1 9 ( 2 1 − i 1 + i 1 ) \begin{aligned} &(1)求A的谱分解:\\ &\quad A有特征多项式 \vert A-\lambda I \vert=\left| \begin{matrix} 2-\lambda&1-i\\1+i&1-\lambda \end{matrix} \right|=(2-\lambda)(1-\lambda)-2=\lambda(\lambda-3)\Rightarrow \lambda(A)=\{3,0\}\\ &\quad G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{3}\left( \begin{matrix} 2&1-i\\1+i&1 \end{matrix} \right),G_2=I-G_1=\frac{1}{3}\left( \begin{matrix} 1&1-i\\-1-i&2 \end{matrix} \right)\\ &\quad 可得谱分解 A=3G_1+0G_2\\ &(2)A^+=3^+G_1=\frac{1}{3}G_1=\frac{1}{9}\left( \begin{matrix} 2&1-i\\1+i&1 \end{matrix} \right)\\ &验证:\\ &\quad (1-i)r_2=r_1,即A为秩1公式,故有A^+=\frac{1}{\sum\vert a_{ij}\vert^2}\left( \begin{matrix} 2&1+i\\1-i&1 \end{matrix} \right)=\frac{1}{9}\left( \begin{matrix} 2&1-i\\1+i&1 \end{matrix} \right) \end{aligned} (1)求A的谱分解:A有特征多项式∣A−λI∣=∣∣∣∣2−λ1+i1−i1−λ∣∣∣∣=(2−λ)(1−λ)−2=λ(λ−3)⇒λ(A)={3,0}G1=λ1−λ2A−λ2I=31(21+i1−i1),G2=I−G1=31(1−1−i1−i2)可得谱分解A=3G1+0G2(2)A+=3+G1=31G1=91(21+i1−i1)验证:(1−i)r2=r1,即A为秩1公式,故有A+=∑∣aij∣21(21−i1+i1)=91(21+i1−i1)
g. 高低分解公式(第二公式)
引理
高低阵引理:
高低阵消去性质:
Hermite性质:
高低广逆公式
高 阵 公 式 : 若 A = A m × r 为 列 满 秩 阵 ( 高 阵 ) , 则 有 加 号 逆 A + = ( A H A ) − 1 A H , 且 A + A = I 低 阵 公 式 : 若 A = A r × n 为 行 满 秩 阵 ( 低 阵 ) , 则 有 加 号 逆 A + = A H ( A A H ) − 1 , 且 A A + = I \begin{aligned} &高阵公式:若A=A_{m\times r} 为列满秩阵(高阵),则有加号逆 A^+=(A^HA)^{-1}A^H,且A^+A=I\\ &低阵公式:若A=A_{r\times n} 为行满秩阵(低阵),则有加号逆 A^+=A^H(AA^H)^{-1},且AA^+=I \end{aligned} 高阵公式:若A=Am×r为列满秩阵(高阵),则有加号逆A+=(AHA)−1AH,且A+A=I低阵公式:若A=Ar×n为行满秩阵(低阵),则有加号逆A+=AH(AAH)−1,且AA+=I
eg
由 高 阵 公 式 : A + = ( A H A ) − 1 A H , 计 算 可 得 A H A = ( 2 0 0 1 ) , ( A H A ) − 1 = 1 2 ( 1 0 0 2 ) , 可 得 A + = ( A H A ) − 1 A H = 1 2 ( 1 0 0 2 ) ( 1 0 1 0 1 0 ) = 1 2 ( 1 0 1 0 2 0 ) , 可 验 证 A + A = I \begin{aligned} &由高阵公式:A^+=(A^HA)^{-1}A^H,计算可得 A^HA=\left( \begin{matrix} 2&0\\0&1 \end{matrix} \right),(A^HA)^{-1}=\frac{1}{2}\left( \begin{matrix} 1&0\\0&2 \end{matrix} \right),\\ &可得A^+=(A^HA)^{-1}A^H=\frac{1}{2}\left( \begin{matrix} 1&0\\0&2 \end{matrix} \right)\left( \begin{matrix} 1&0&1\\0&1&0 \end{matrix} \right)=\frac{1}{2}\left( \begin{matrix} 1&0&1\\0&2&0 \end{matrix} \right),可验证\\ &A^+A=I \end{aligned} 由高阵公式:A+=(AHA)−1AH,计算可得AHA=(2001),(AHA)−1=21(1002),可得A+=(AHA)−1AH=21(1002)(100110)=21(100210),可验证A+A=I
由 于 B = A H , 则 B + = ( A H ) + = ( A + ) H = 1 2 ( 1 0 0 2 1 0 ) \begin{aligned} &由于B=A^H,则B^+=(A^H)^+=(A^+)^H=\frac{1}{2}\left( \begin{matrix} 1&0\\0&2\\1&0 \end{matrix} \right) \end{aligned} 由于B=AH,则B+=(AH)+=(A+)H=21⎝⎛101020⎠⎞
由 低 阵 公 式 A + = A H ( A A H ) − 1 , A A H = ( 2 1 1 2 ) , ( A A H ) − 1 = 1 3 ( 2 − 1 − 1 2 ) A + = A H ( A A H ) − 1 = 1 3 ( 1 1 − 1 2 2 − 1 ) 由 于 B = A H , B + = ( A H ) + = ( A + ) H = 1 3 ( 1 − 1 2 1 2 − 1 ) \begin{aligned} &由低阵公式A^+=A^H(AA^H)^{-1},AA^H=\left( \begin{matrix} 2&1\\1&2 \end{matrix} \right),(AA^H)^{-1}=\frac{1}{3}\left( \begin{matrix} 2&-1\\-1&2 \end{matrix} \right)\\ &A^+=A^H(AA^H)^{-1}=\frac{1}{3}\left( \begin{matrix} 1&1\\-1&2\\2&-1 \end{matrix} \right)\\ &由于B=A^H,B^+=(A^H)^+=(A^+)^H=\frac{1}{3}\left( \begin{matrix} 1&-1&2\\1&2&-1 \end{matrix} \right) \end{aligned} 由低阵公式A+=AH(AAH)−1,AAH=(2112),(AAH)−1=31(2−1−12)A+=AH(AAH)−1=31⎝⎛1−1212−1⎠⎞由于B=AH,B+=(AH)+=(A+)H=31(11−122−1)
A + A^+ A+ 第二公式(高低分解公式)
若 有 高 低 分 解 A = B C , 则 有 公 式 : A + = C + B + , 其 中 B + = ( B H B ) − 1 B H , C + = A H ( A A H ) − 1 且 有 B + B = I , C C + = I \begin{aligned} &若有高低分解 A=BC,则有公式:A^+=C^+B^+,其中B^+=(B^HB)^{-1}B^H,C^+=A^H(AA^H)^{-1}\\ &且有B^+B=I,CC^+=I \end{aligned} 若有高低分解A=BC,则有公式:A+=C+B+,其中B+=(BHB)−1BH,C+=AH(AAH)−1且有B+B=I,CC+=I
注
( B C ) + (BC)^+ (BC)+ 一般不成立,只有在高低分解时才成立
eg
∵ A = ( 1 0 0 0 1 − 1 0 0 0 0 0 0 ) , 故 选 第 1 , 2 列 作 为 高 阵 , B = ( 1 0 0 1 1 0 2 1 ) , C = ( 1 0 0 0 1 − 1 ) , A = B C ( 高 低 分 解 ) ( B H B ) − 1 = 1 4 ( 1 − 1 − 1 3 ) , ( C C H ) − 1 = 1 2 ( 2 0 0 1 ) , B + = ( B H B ) − 1 B H = 1 4 ( 1 − 1 − 1 3 ) ( 1 0 1 2 0 1 0 1 ) = 1 4 ( 1 0 1 1 − 1 3 − 1 1 ) , C + = C H ( C C H ) − 1 = 1 2 ( 2 0 0 1 0 − 1 ) , A = C + B + = 1 8 ( 2 − 2 2 2 − 1 3 − 1 1 1 − 3 1 − 1 ) \begin{aligned} &\because A=\left( \begin{matrix} 1&0&0\\0&1&-1\\0&0&0\\0&0&0 \end{matrix} \right),故选第1,2列作为高阵,B=\left( \begin{matrix} 1&0\\0&1\\1&0\\2&1 \end{matrix} \right),C=\left( \begin{matrix} 1&0&0\\0&1&-1 \end{matrix} \right),A=BC(高低分解)\\ &(B^HB)^{-1}=\frac{1}{4}\left( \begin{matrix} 1&-1\\-1&3 \end{matrix} \right),(CC^H)^{-1}=\frac{1}{2}\left( \begin{matrix} 2&0\\0&1 \end{matrix} \right),\\ &B^+=(B^HB)^{-1}B^H=\frac{1}{4}\left( \begin{matrix} 1&-1\\-1&3 \end{matrix} \right)\left( \begin{matrix} 1&0&1&2\\0&1&0&1 \end{matrix} \right)=\frac{1}{4}\left( \begin{matrix} 1&0&1&1\\-1&3&-1&1 \end{matrix} \right),\\ &C^+=C^H(CC^H)^{-1}=\frac{1}{2}\left( \begin{matrix} 2&0\\0&1\\0&-1 \end{matrix} \right),\\ &A=C^+B^+=\frac{1}{8}\left( \begin{matrix} 2&-2&2&2\\-1&3&-1&1\\1&-3&1&-1 \end{matrix} \right) \end{aligned} ∵A=⎝⎜⎜⎛100001000−100⎠⎟⎟⎞,故选第1,2列作为高阵,B=⎝⎜⎜⎛10120101⎠⎟⎟⎞,C=(10010−1),A=BC(高低分解)(BHB)−1=41(1−1−13),(CCH)−1=21(2001),B+=(BHB)−1BH=41(1−1−13)(10011021)=41(1−1031−111),C+=CH(CCH)−1=21⎝⎛20001−1⎠⎞,A=C+B+=81⎝⎛2−11−23−32−1121−1⎠⎞
h. 第三公式
A + = ( A H A ) + A H A^+=(A^HA)^+A^H A+=(AHA)+AH
应用
eg
i. 张量分解公式
( A ⊗ B ) + = A + ⊗ B + (A\otimes B)^+=A^+\otimes B^+ (A⊗B)+=A+⊗B+
j. 分块公式
( A 0 ) + = ( A + , 0 ) , ( A , 0 ) + = ( A + , 0 ) ( A 1 0 0 A 2 ) + = ( A 1 + 0 0 A 2 + ) ( 0 A 1 A 2 0 ) + = ( 0 A 1 + A 2 + 0 ) ( A A A ) + = 1 3 ( A + , A + , A + ) ( A , A , A ) + = 1 3 ( A + A + A + ) ( A A A A ) + = 1 4 ( A + A + A + A + ) \left( \begin{matrix} A\\0 \end{matrix} \right)^+=\left(A^+,0\right),(A,0)^+=\left( \begin{matrix} A^+,0 \end{matrix} \right)\\ \left( \begin{matrix} A_1&0\\0&A_2 \end{matrix} \right)^+=\left( \begin{matrix} A_1^+&0\\0&A_2^+ \end{matrix} \right)\\ \left( \begin{matrix} 0&A_1\\A_2&0 \end{matrix} \right)^+=\left( \begin{matrix} 0&A_1^+\\A_2^+&0 \end{matrix} \right)\\ \left( \begin{matrix} A\\A\\A \end{matrix} \right)^+=\frac{1}{3}\left(A^+,A^+,A^+\right)\\ (A,A,A)^+=\frac{1}{3}\left( \begin{matrix} A^+\\A^+\\A^+ \end{matrix} \right)\\ \left( \begin{matrix} A&A\\A&A \end{matrix} \right)^+=\frac{1}{4}\left( \begin{matrix} A^+&A^+\\A^+&A^+ \end{matrix} \right) (A0)+=(A+,0),(A,0)+=(A+,0)(A100A2)+=(A1+00A2+)(0A2A10)+=(0A2+A1+0)⎝⎛AAA⎠⎞+=31(A+,A+,A+)(A,A,A)+=31⎝⎛A+A+A+⎠⎞(AAAA)+=41(A+A+A+A+)
eg
A = ( D 0 ) , D 为 低 阵 , D + = D H ( D D H ) − 1 = 1 2 ( 1 0 0 2 1 0 ) , A + = ( D + 0 ) = ( 1 2 0 0 0 1 0 1 2 0 0 ) \begin{aligned} &A=\left( \begin{matrix} D\\0 \end{matrix} \right),D为低阵,D^+=D^H(DD^H)^{-1}=\frac{1}{2}\left( \begin{matrix} 1&0\\0&2\\1&0 \end{matrix} \right),A^+=\left( \begin{matrix} D^+&0 \end{matrix} \right)=\left( \begin{matrix} \frac{1}{2}&0&0\\0&1&0\\\frac{1}{2}&0&0 \end{matrix} \right) \end{aligned} A=(D0),D为低阵,D+=DH(DDH)−1=21⎝⎛101020⎠⎞,A+=(D+0)=⎝⎛21021010000⎠⎞
eg