深度学习优化器演化史
《深度学习优化器演化史》
不同深度学习的优化器有时候对于训练模型来说可能会有很大的差异,有时候选对了优化器就能够有事半功倍的效果,那么如果选择各种优化器呢,本文来简单剖析一下深度学习优化器的原理。
Key Words:Momentum、AdaGrad、Adam…
Beijing, 2020
Agile Pioneer
Optimizer
on-line : one pair of (x, y) at a time step,add new data any time.
off-line : pour all (x, y) into the memory for train at every time step.
参数优化 = Learning Rate + Gradient
Notation
- η \eta η 学习率
- W W W、 θ \theta θ 参数
- ∇ θ t \nabla_{\theta_t} ∇θt、 g t g^t gt 第t个时间步的参数 θ \theta θ的梯度
- m t + 1 m_{t+1} mt+1 从第0个时间步积累到第t个时间步骤的动量,用于计算 θ t + 1 \theta_{t+1} θt+1
- RMS: Root mean square
Gradient Descent [Cauchy, 1847]
梯度下降是用于优化的最常用的算法,也是目前优化神经网络最普遍的方法。就每次计算梯度所用的数据量而言,梯度下降法有三种形态:
-
基于全量数据的梯度下降,aka batch gradient descent
θ = θ − η ⋅ ∇ θ J ( θ ) \theta = \theta - \eta \cdot \nabla_{\theta} J(\theta) θ=θ−η⋅∇θJ(θ)
1.1 对于内存放不下的全量数据无法进行训练,而且无法对随时有新的例子的情况进行online训练。
1.2 对于凸面可以收敛到全局最小值,而非凸面会陷入局部最小值 -
随机梯度下降(SGD)
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i ) ; y ( i ) ) \theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x^{(i)};y^{(i)}) θ=θ−η⋅∇θJ(θ;x(i);y(i))
2.1 随机打乱样本,对每个训练样本计算梯度来更新参数,可以online学习
2.2 SGD速度更快,但是会出现loss严重的震荡,可能会震荡到更好的局部最小值,或者全局最小值,但是收敛的过程很难控制。
2.3 通过逐渐降低学习率,SGD会趋向于和BGD一样的趋势,对于凸面会找到全局最小值,非凸面也可能会陷入局部最小值 -
Mini-Batch梯度下降
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i : i + n ) ; y ( i : i + n ) ) \theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x^{(i:i+n)};y^{(i:i+n)}) θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n))
3.1 以固定的batch-size样本训练模型,可以online学习
3.2 减少了参数更新的方差,能够更稳定的收敛
而梯度下降的各种方法同时面临如下问题:
- 选择一个合适的学习率是很难的。过小则收敛太慢,过大则在最优解附近震荡收敛困难。(Momentum)
- 如果使用学习率的计划,用于在训练过程中调整学习率,那么一个合适的学习率改变计划就是一个难题了,因为很难适应数据的特性。
- 所有的参数如果都使用相同的学习率是有问题的,如果我们的数据是稀疏的,并且我们的特征的频率相差很大,我们不想以相同的程度更新所有的参数,对于出现较少的特征可能需要更大的学习率。(Adagrad)
- 最大的挑战是对于非凸平面的局部最小值的问题,或者是陷入鞍点的问题。这些鞍点的一个特征是周围的梯度都是接近于0的,所以导致梯度下降失效了。
Gradient Descent with momentum [Rumelhart, et al., Nature’1986]
Momentnum
解决SGD遇到梯度近似为0的位置会陷入的问题
动力项是一个能够在梯度方向一致的情况下加速SGD的方法,并且能够抑制震荡。通过增加一项梯度累加项,对历史的梯度进行累积,就像从山上向下滚动的小球一样,在下山的过程中小球的动量会越来越大,速度就会越来越快(其中的系数 γ \gamma γ可以理解为空气阻力)。在参数优化的过程中,如果动量和梯度的方向相同,那么速度就会越来越快,而动量和梯度的方向相反时,速度就会越来越慢。因此,可以更快的收敛,并减少震荡。
v t = γ v t − 1 + η ∇ θ J ( θ ) v_t = \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta) vt=γvt−1+η∇θJ(θ)
θ = θ − v t \theta = \theta - v_t θ=θ−vt
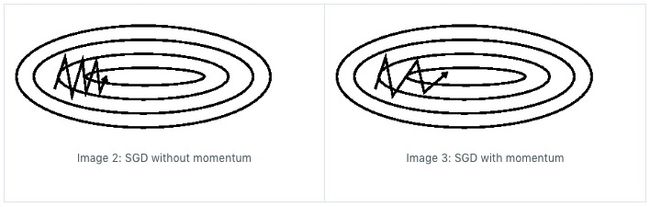
γ \gamma γ 取值一般为0.9
NAG (Nesterov Accelerated Gradient)
加入动量后的小球会盲目地跟从下坡的梯度,容易发生错误,我们可以把小球变得更加聪明。也就是当小球知道对面是上坡的时候就提前的降低速度,而不是冲上另一个坡。NAG就是赋予动量以先知的方法。
即利用 θ − γ v t − 1 \theta - \gamma v_{t-1} θ−γvt−1 作为参数下个位置的估计值,所以在计算梯度时,不是在当前位置,而是未来的位置上。我们的参数将要去哪是个复杂的问题,我们现在就可以有效地提前通过估计下一个位置的值来调整参数的位置。
v t = γ v t − 1 + η ∇ θ J ( θ − γ v t − 1 ) v_t = \gamma v_{t-1} + \eta \nabla_{\theta}J(\theta - \gamma v_{t-1}) vt=γvt−1+η∇θJ(θ−γvt−1)
θ = θ − v t \theta = \theta - v_t θ=θ−vt

蓝色是 Momentum 的过程,会先计算当前的梯度,然后在更新后的累积梯度后会有一个大的跳跃。而 NAG 会直接先在前一步的累积梯度上有一个大的跳跃(棕色线),然后衡量一下梯度做一下修正(红色线),这种预期的更新可以避免我们走的太快,并加速响应。最终的优化路径为(绿色线)。NAG可以显著的提高RNN的效果。
目前为止,我们可以做到,在更新梯度时顺应loss function的梯度来调整速度,并且对 SGD 进行加速。我们还希望可以根据参数的重要性而对不同的参数进行不同程度的更新。
AdaGrad (Adaptive gradient algorithm)[Duchi, et.al, JMLR 2011]
核心思想:对频繁出现的特征执行更小的参数更新(低学习率),对于出现较少的特征予以更大的参数更新。所以该方法非常适用于处理稀疏数据,而且很大程度上提高了SGD的鲁棒性。
对于优化问题来说,应该是随着梯度的增大,我们的步长也是增大的,但是Adagrad中随着梯度的增大,分母开始增大,学习的步长反而减少了,因为在优化的最初阶段,参数距离最优解的距离是很远的,所以需要较大的学习步长,但是随着参数更新的次数增多,我们认为越来越接近最优解,所以学习速率也就随之变慢。和学习率的衰减的道理是一致的。
Adagrad:
W t + 1 = W t − η t σ t g t W^{t+1} = W^t - \frac{\eta^t}{\sigma^t} g^t Wt+1=Wt−σtηtgt
Learning Rate decay:
η t = η t + 1 \eta^t = \frac{\eta}{\sqrt{t + 1}} ηt=t+1η
Root mean square of its previous derivatives:
σ t = 1 t + 1 ∑ i = 0 t ( g i ) 2 \sigma^t = \sqrt{\frac{1}{t + 1} \sum_{i=0}^t (g_i)^2} σt=t+11i=0∑t(gi)2
final:
W t + 1 = W t − η ∑ i = 1 t ( g i ) 2 + ϵ ⨀ g t W_{t+1} = W_t - \frac{\eta}{\sqrt{\sum^t_{i=1}(g_{i})^2 + \epsilon}} \bigodot g_t Wt+1=Wt−∑i=1t(gi)2+ϵη⨀gt
为什么要除以梯度的平方和?
首先要知道AdaGrad其实是对于参数变换较快(梯度较大)的参数,用以较小的学习率,而对于参数变化较小(梯度较小)的参数,用以较大的学习率。所以考虑如下问题:
- 对于参数1而言有两个点a和b,a的梯度大于b,那么可以认为a距离最优解较b远
- 而如果参数1和参数2相比,比如此时的点,参数1的梯度大于参数2的梯度,并不代表距离一定参数1较远
- 要考虑到二阶导数值,距离最优解的距离和二阶导数值呈反比
- 以 3 ∗ x 2 3 * x^2 3∗x2 和 x 2 x^2 x2为例,前者梯度较高,后者梯度较低,前者和后者梯度相同的时候,后者距离最优解较远(需要较大步长),所以用除以其二阶导数值作为学习率的调整较为合适
- 而计算二阶导数较为费时,所以利用一阶导数值的平方来估计其二阶导数值,所以除以梯度的平方和

AdaGrad的实现代码:
1. 记录每个参数的梯度值,并求其平方和
2. 更新当前参数时 = 学习率 / 该参数历史梯度的均方根 * 梯度
class AdaGrad:
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, value in params.items():
self.h[key] = np.zeros_like(value)
for key in params.keys():
self.h[key] += grads[key] * grads[key] # gt^2
# 1e-07 avoid denominator to 0
params[key] -= self.learning_rate / (sqrt(self.h[key]) + 1e-07)* grads[key]
缺点:
- 分母增加的每一项都是正数,在训练的时候学习率是单调递减的,训练初期鼓励收敛,训练后期阻碍收敛
- 需要设置一个合适的全局初始学习率
- 如何解决上述的缺点呢?-> AdaDelta or RMSprop
AdaDelta
Adadelta是AdaGrad方法的一个扩展,用于减少AdaGrad的学习率单调下降的严重缺陷。其策略是通过固定窗口对参数过往的参数梯度进行积累,而不是参数过往所有梯度。
其具体的做法是对过往的梯度平方计算均值,并通过定义个系数使过往的参数梯度平方衰减保存, E [ g 2 ] t E[ g^2 ]_t E[g2]t 表示第t个时间步的时候的加权均值,即对当前的梯度平方乘以 1 − γ 1-\gamma 1−γ ,而对过往的梯度平方的均值乘以 γ \gamma γ。
E [ g 2 ] t = γ E [ g 2 ] t − 1 + ( 1 − γ ) g t 2 E[ g^2 ]_t = \gamma E[ g^2 ]_{t - 1} + ( 1 - \gamma)g^2_t E[g2]t=γE[g2]t−1+(1−γ)gt2
γ \gamma γ 类似于动量项,取值0.9左右。
AdaDelta 公式推演:
Δ θ t = − η E [ g 2 ] t + ϵ g t \Delta \theta_t = - \frac{ \eta }{\sqrt{E[ g^2 ]_t + \epsilon }} g_t Δθt=−E[g2]t+ϵηgt
均方根可以用RMS来表示:
R M S ( Δ [ θ ] t ) = E [ Δ θ 2 ] t + ϵ RMS(\Delta [ \theta]_t) = \sqrt{E[ \Delta \theta^2 ]_t + \epsilon} RMS(Δ[θ]t)=E[Δθ2]t+ϵ
AdaDelta算法,采用Hessian矩阵的对角线近似Hessian矩阵,即学习率可以替换为:
E [ Δ θ 2 ] t = γ E [ Δ θ 2 ] t − 1 + ( 1 − γ ) Δ θ t 2 E[\Delta \theta^2]_t = \gamma E[\Delta\theta^2]_{t-1} + (1 - \gamma)\Delta \theta^2_t E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθt2
平方根替换为RMS为:
R M S [ Δ θ ] t = E [ Δ θ 2 ] t + ϵ RMS[\Delta \theta]_t = \sqrt{E[ \Delta \theta^2 ]_t + \epsilon} RMS[Δθ]t=E[Δθ2]t+ϵ
因为 R M S [ Δ θ ] t RMS[ \Delta \theta ]_t RMS[Δθ]t是未知的,所以我们用之前时间步的RMS来估计它,用于替换学习率 η \eta η,最终的AdaDelta的表达式如下:
Δ θ t = − R M S [ Δ θ ] t − 1 R M S [ g ] t g t \Delta \theta_t = - \frac{RMS[ \Delta \theta ]_{t-1}}{RMS[ g ]_t} g_t Δθt=−RMS[g]tRMS[Δθ]t−1gt
update:
θ t + 1 = θ t + Δ θ t \theta_{t+1} = \theta_t + \Delta \theta_t θt+1=θt+Δθt
算法:

使用Adadelta就不需要设置初始的学习率了
RMSprop [Geoff Hinton 2013]
RMSprop是由Geoff Hinton在讲课中提出的自适应学习率的方法。RMSprop和AdaDelta几乎是同时出现的,用于解决Adagrad’s的学习率快速消失的问题。RMSprop与AdaDelta的第一种形式是一致的:
E [ g 2 ] t = γ E [ g 2 ] t − 1 + ( 1 − γ ) g t 2 E[ g^2 ]_t = \gamma E[ g^2 ]_{t - 1} + ( 1 - \gamma)g^2_t E[g2]t=γE[g2]t−1+(1−γ)gt2
θ t + 1 = θ t − η E [ g 2 ] t + ϵ g t \theta_{t + 1} = \theta_t - \frac{ \eta }{\sqrt{E[ g^2 ]_t + \epsilon }} g_t θt+1=θt−E[g2]t+ϵηgt
使用指数加权平均,旨在消除梯度下降中的摆动,与Momentum的效果一样,某一维度的导数比较大,则指数加权平均就大,某一维度的导数比较小,则其指数加权平均就小,这样就保证了各维度导数都在一个量级,进而减少了摆动。允许使用一个更大的学习率 η \eta η。
Hiton建议 γ = 0.9 \gamma=0.9 γ=0.9, η = 0.001 \eta = 0.001 η=0.001 是一个好的默认值。
Adam(Adaptive Moment Estimation)[Kingma, et al.,ICLR 2015]
Adam = RMSprop + Momentum
Adam也是一种计算每个参数的自适应学习率的方法:
- 存储了一个过往梯度平方的指数衰减的平均值 v t v_t vt类似于AdaDelta和RMSprop
- 存储了一个过往的梯度的指数衰减平均值 m t m_t mt类似于Momentum
所以Adam更像是一个从山上向下滚动的带有摩擦力的重球,因此更容易在平坦的误差平面取得最小值。过往的梯度衰减平均值 m t m_t mt和平方梯度衰减平均值 v t v_t vt的计算方式如下:
first moment:
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t mt=β1mt−1+(1−β1)gt
second moment:
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2 vt=β2vt−1+(1−β2)gt2
m t m_t mt 是梯度的一阶矩估计(均值), v t v_t vt 是梯度的二阶原点矩估计。所以算法名为“自适应矩估计”优化算法。算法使用移动平均法进行对一阶矩和二阶矩进行估计,从上面的式子上可以看出滑动平均的前几步严重的向 m 0 m_0 m0倾斜,所以为了修正这个去掉初始化值的影响,比如在第一步,我们移除 β m 0 \beta m_0 βm0,然后除以 ( 1 − β ) (1 - \beta) (1−β) 即 m 1 ^ = ( m 1 − β m 0 ) / ( 1 − β ) \hat{m_1} =(m_1 - \beta m_0) / (1-\beta) m1^=(m1−βm0)/(1−β),当 m 1 = 0 m_1=0 m1=0那么 m 1 ^ = m 1 / ( 1 − β ) \hat{m_1} = m1 / (1 - \beta) m1^=m1/(1−β), v t v_t vt 同理。
m t ^ = m t 1 − β 1 t \hat{m_t} = \frac{m_t}{1 - \beta^t_1} mt^=1−β1tmt
v t ^ = v t 1 − β 2 t \hat{v_t} = \frac{v_t}{1 - \beta^t_2} vt^=1−β2tvt
update:
θ t + 1 = θ t − η v t ^ + ϵ m t ^ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t} + \epsilon}}\hat{m_t} θt+1=θt−vt^+ϵηmt^
超参数建议值: β 1 = 0.9 , β 2 = 0.999 , ϵ = 10 e − 8 \beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10e-8 β1=0.9,β2=0.999,ϵ=10e−8
b e t a 1 beta_1 beta1 一阶矩的系数,类似于Momentum的梯度衰减平均值
b e t a 2 beta_2 beta2 二阶矩的系数,类似于RMSprop或AdaDelta的梯度平方的衰减平均值
Adam效果实际使用起来更好。
## 各个优化方法的可视化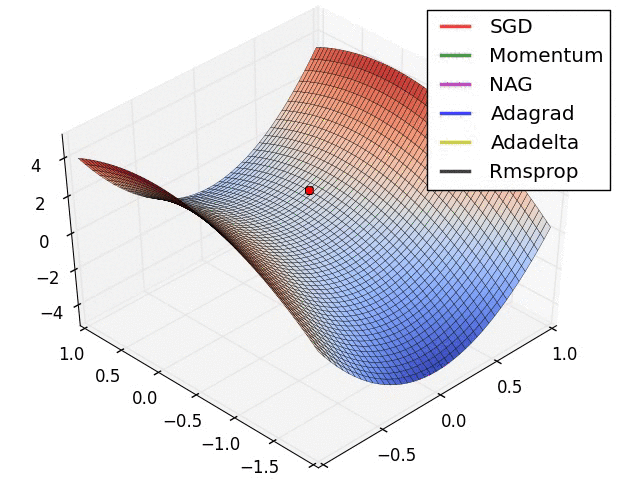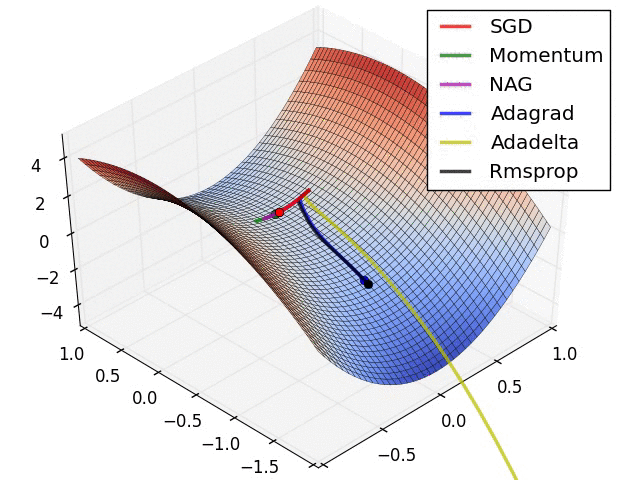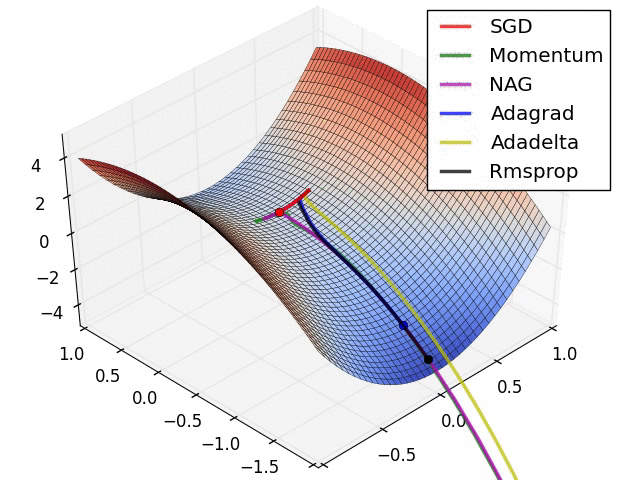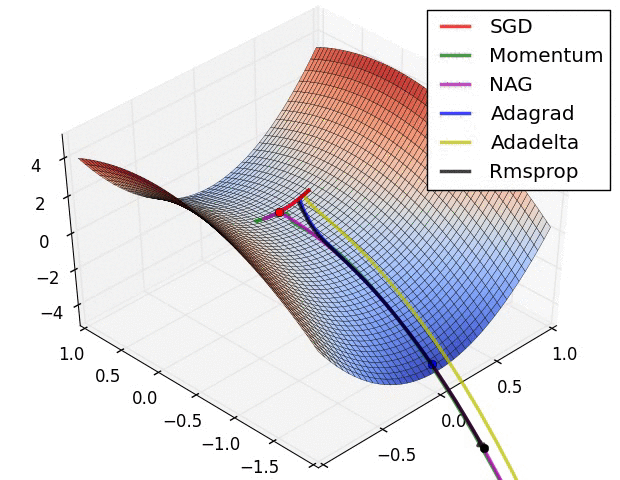

优化器选择建议
-
如果数据是稀疏的,就用自适用方法,即 Adagrad, Adadelta, RMSprop, Adam
-
RMSprop, Adadelta, Adam 在很多情况下的效果是相似的
-
Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum的衰减平均值
-
随着梯度变的稀疏,Adam 比 RMSprop 效果会好。
-
很多论文里都会用 SGD,没有 momentum 等。SGD 虽然能达到极小值,但是比其它算法用的时间长,而且可能会被困在鞍点。
-
如果需要更快的收敛,或者是训练更深更复杂的神经网络,需要用一种自适应的算法。
-
整体来讲,Adam 是最好的选择
三省吾身
-
从最初的梯度下降根据一次更新梯度的样本数目分为了三种,以及两类online、offline
-
SGD存在的问题是易陷入鞍点,以及学习过慢,震荡较为严重
-
Momentum会改善陷入鞍点的情况,但是会冲上loss较高的山坡
-
NAG实际上让Momentum变得圆滑,但是实际不常用
-
AdaGrad打开了新世界的大门,即对不同的参数用以不用的学习步长,实际上也确实是这样的,因为有的参数变换较为剧烈,而有的又较为缓慢,用同一个学习率确实不合适
-
AdaGrad的缺陷较为明显,对梯度的二阶矩估计值进行疯狂积累始来改善学习率始终不是办法,所以AdaDelta和RMSprop出现了,AdaDelta思考明显更多,而RMSprob是Hinton讲课的时候提出的,两者的很像,都是利用梯度的二阶矩估计值进行平均衰减来调整学习率,且避免学习率快速下降为0的情况。
-
Adam 自适应矩估计优化算法,站在巨人的肩膀上,高屋建瓴的借用了Momentum的平均衰减来解决鞍点问题,利用二阶矩估计的平均衰减来解决不同参数的不同学习步长问题。
参考
Optimizer 1
https://ruder.io/optimizing-gradient-descent/index.html
Optimizer 2
https://www.cnblogs.com/guoyaohua/p/8542554.html
Optimizer 3
https://zhuanlan.zhihu.com/p/61955391
AdaGrad
https://blog.csdn.net/weixin_44478378/article/details/101167706
AdaDelta
https://blog.csdn.net/XiangJiaoJun_/article/details/83960136
Matrix-Vector Products
https://www.jianshu.com/p/87b19b08f8bc