实验三 算符优先分析算法的设计与实现
实验三 算符优先分析算法的设计与实现(8学时)
一、 实验目的
根据算符优先分析法,对表达式进行语法分析,使其能够判断一个表达式是否正确。通过算符优先分析方法的实现,加深对自下而上语法分析方法的理解。
二、 实验要求
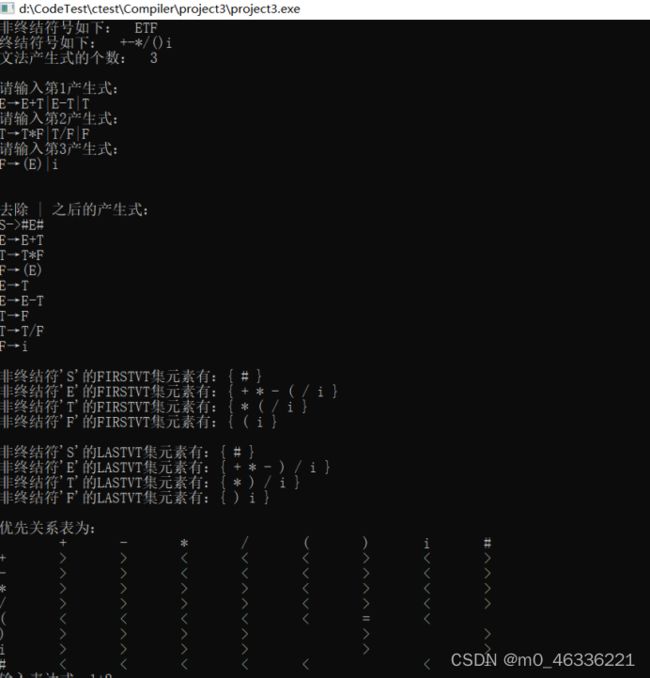
1、输入文法。可以是如下算术表达式的文法(你可以根据需要适当改变):
E→E+T|E-T|T
T→T*F|T/F|F
F→(E)|i
2、对给定表达式进行分析,输出表达式正确与否的判断。
程序输入/输出示例:
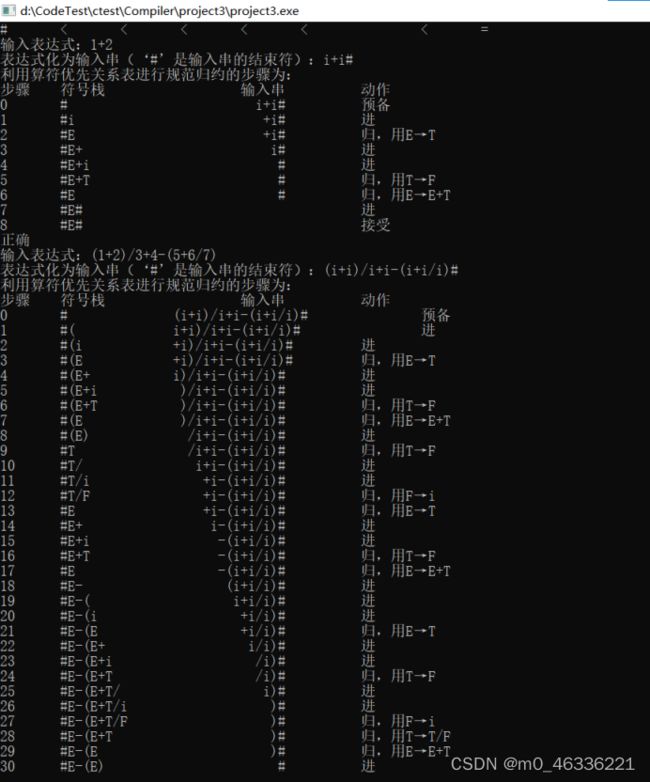
输入:1+2
输出:正确
输入:(1+2)/3+4-(5+6/7)
输出:正确
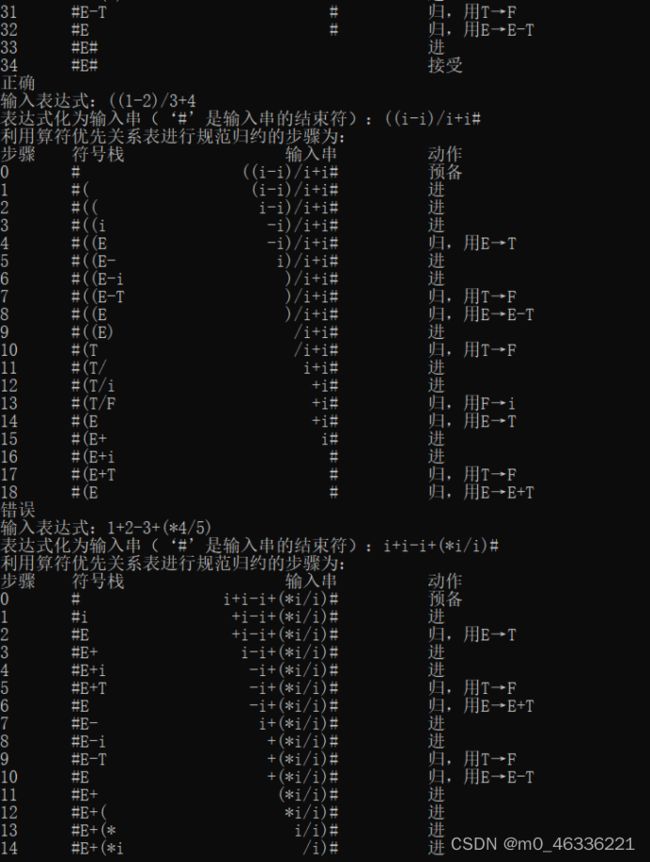
输入:((1-2)/3+4
输出:错误
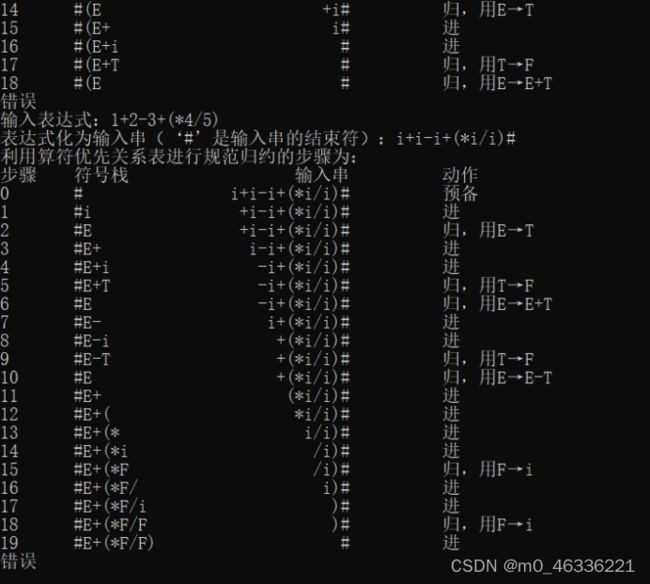
输入:1+2-3+(*4/5)
输出:错误
三、实验步骤
1、参考数据结构
char *VN=0,*VT=0;//非终结符和终结符数组
char firstvt[N][N],lastvt[N][N],table[N][N];
typedef struct //符号对(P,a)
{
char Vn;
char Vt;
} VN_VT;
typedef struct //栈
{
VN_VT *top;
VN_VT *bollow;
int size;
}stack;
2、根据文法求FIRSTVT集和LASTVT集
给定一个上下文无关文法,根据算法设计一个程序,求文法中每个非终结符的FirstVT 集和LastVT 集。
算符描述如下:
/求 FirstVT 集的算法/
PROCEDURE insert(P,a);
IF not F[P,a] then
begin
F[P,a] = true; //(P,a)进栈
end;
Procedure FirstVT;
Begin
for 对每个非终结符 P和终结符 a do
F[P,a] = false
for 对每个形如 P a…或 P→Qa…的产生式 do
Insert(P,a)
while stack 非空
begin
栈顶项出栈,记为(Q,a)
for 对每条形如 P→Q…的产生式 do
insert(P,a)
end;
end.
同理,可构造计算LASTVT的算法。
3、构造算符优先分析表
依据文法和求出的相应FirstVT和 LastVT 集生成算符优先分析表。
算法描述如下:
for 每个形如 P->X1X2…Xn的产生式 do
for i =1 to n-1 do
begin
if Xi和Xi+1都是终结符 then
Xi = Xi+1
if i<= n-2, Xi和Xi+2 是终结符, 但Xi+1 为非终结符 then
Xi = Xi+2
if Xi为终结符, Xi+1为非终结符 then
for FirstVT 中的每个元素 a do
Xi < a ;
if Xi为非终结符, Xi+1为终结符 then
for LastVT 中的每个元素 a do
a > Xi+1 ;
end
4、构造总控程序
算法描述如下:
stack S;
k = 1; //符号栈S的使用深度
S[k] = ‘#’
REPEAT
把下一个输入符号读进a中;
If S[k] VT then j = k else j = k-1;
While S[j] > a do
Begin
Repeat
Q = S[j];
if S[j-1] VT then j = j-1 else j = j-2
until S[j] < Q;
把S[j+1]…S[k]归约为某个N,并输出归约为哪个符号;
K = j+1;
S[k] = N;
end of while
if S[j] < a or S[j] = a then
begin k = k+1; S[k] = a end
else error //调用出错诊察程序
until a = ‘#’
5、对给定的表达式,给出准确与否的分析过程
6、给出表达式的计算结果。(本步骤可选作)
四、实验报告要求
1.写出编程思路、源代码(或流程图);
#include
(non_ter.find(gramOldSet[cnt].formula[i + 1]) != -1)){
int cnt1 = 0;//FIRSTVT的位置指针
while(cnt1 < FIRSTVT[non_ter.find(gramOldSet[cnt].formula[i + 1])].length()){
x_Cor = terSymbol.find(gramOldSet[cnt].formula[i]);
y_Cor = terSymbol.find(FIRSTVT[non_ter.find(gramOldSet[cnt].formula[i + 1])][cnt1]);
M[x_Cor][y_Cor] = '<';
cnt1++;
}
}
if((terSymbol.find(gramOldSet[cnt].formula[i]) == -1) &&//Xi为终结符而Xi+1为非终结符,LASTVT(Xi)中的a>Xi
(non_ter.find(gramOldSet[cnt].formula[i + 1]) == -1)){
int cnt2 = 0;//LASTVT的位置指针
do{
x_Cor = terSymbol.find(LASTVT[non_ter.find(gramOldSet[cnt].formula[i])][cnt2]);
y_Cor = terSymbol.find(gramOldSet[cnt].formula[i+1]);
M[x_Cor][y_Cor] = '>';
cnt2++;
}while(cnt2 < LASTVT[non_ter.find(gramOldSet[cnt].formula[i])].length());
}
}
}
cnt++;
}while(cnt < n);
cout<<"优先关系表为:"<<endl;
cout<<"\t";
for(int i = 0; i < terSymbol.length(); i++){
cout<<terSymbol[i]<<"\t";
}
cout<<endl;
for(int i = 0;i < terSymbol.length();i++){
cout<<terSymbol[i]<<"\t";
for(int j = 0;j < terSymbol.length()+1;j++)
cout<<M[i][j]<<"\t";
cout<<endl;
}
}
void allContronl(){//总控程序
cout<<"输入表达式:";
cin>>form;//表达式
// cout<<"待分析的输入串为(‘#’是输入串的结束符):";
str_cin = dealForm(form);//输入串
cout<<"表达式化为输入串(‘#’是输入串的结束符):"<<str_cin<<endl;
// cin>>str_cin;
cout<<"利用算符优先关系表进行规范归约的步骤为:"<<endl;
char a;//当前的输入符a
bool flag1=true;
int j,pos = 0, counter = 1;//pos输入串的指示坐标,counter步骤计数器
cout<<setw(8)<<std::left<<"步骤"<<setw(15)<<std::left<<"符号栈";
cout<<setw(15)<<std::right<<"输入串"<<"\t\t"<<setw(15)<<std::left<<"动作"<<endl;
S.push_back('#');//置初值
cout<<setw(8)<<std::left<<"0"<<setw(15)<<std::left<<PrintStack(S);
cout<<setw(15)<<std::right<<PrintStrCin(str_cin,pos)<<"\t\t"<<setw(15)<<std::left<<"预备"<<endl;
int k = 0;//k代表符号栈的使用深度
// a = str_cin[pos];
do{
char N;//N为归约成的符号
a = str_cin[pos];//把下一个输入符号读进a中
if(terSymbol.find(S[k]) != -1){//S[k]∈Vt
j = k;
}else{
j = k - 1;
}
while(M[terSymbol.find(S[j])][terSymbol.find(a)] == ">"){//S[j] > a
char Q;
string str1;//保存S[j+1]..S[k]
string str_gram;//归约所用式子
do{
Q = S[j];
if(terSymbol.find(S[j-1]) != -1){//S[j-1]∈Vt
j = j - 1;
}else{
j = j - 2;
}
}while(M[terSymbol.find(S[j])][terSymbol.find(Q)] != "<");
bool flag = true;//归约标志
int Maxnum = 0;
for(int i0 = j+1; i0 <= k; i0++)
str1 += S[i0];
while(flag&&Maxnum < 3){
for(int i1 = 0; i1 < n; i1++){
string str2;
str2 = gramOldSet[i1].formula.substr(3);//保存产生式右部
if(str1 == str2){//归约
N = gramOldSet[i1].formula[0];
str_gram = gramOldSet[i1].formula;
str1 = N;
if((S[j] == '/' | S[j] == '*')&&(N == 'F'))
flag = false;
if((S[j] == '+'| S[j] == '-'| a == '*'| a == '/')&&(N == 'T'))
flag = false;
break;
}
}
Maxnum++;
}//把S[j+1]..S[k]归约为某个N}
if(N == ' ') break;
for(int m = j+1; m <= k;m++)//归约
S.pop_back();
k = j+1;
S.push_back(N);
N = ' ';
cout<<setw(8)<<std::left<<counter++<<setw(15)<<std::left<<PrintStack(S);//步骤加1
cout<<setw(15)<<std::right<<PrintStrCin(str_cin,pos)<<"\t\t"<<setw(15)<<std::left<<"归,用"+str_gram<<endl;
}
if((M[terSymbol.find(S[j])][terSymbol.find(a)] == "<") ||
(M[terSymbol.find(S[j])][terSymbol.find(a)] == "=")){//S[j] < a 或 S[j] = a
k++;
S.push_back(a);
++pos;
// a = str_cin[++pos];//把下一个输入符号读进a中
cout<<setw(8)<<std::left<<counter++<<setw(15)<<std::left<<PrintStack(S);//步骤加1
cout<<setw(15)<<std::right<<PrintStrCin(str_cin,pos)<<"\t\t"<<setw(15)<<std::left<<"进"<<endl;
}else{
cout<<"错误"<<endl;
flag1 = false;
break;
}
}while(a != '#');
if((a == '#' ) && flag1){
cout<<setw(8)<<std::left<<counter<<setw(15)<<std::left<<PrintStack(S);
cout<<setw(15)<<std::right<<PrintStrCin(str_cin,pos)<<"\t\t"<<setw(15)<<std::left<<"接受"<<endl;
cout<<"正确"<<endl;
}
}
int main(){
cout<<"非终结符号如下: ";
cin>>non_ter;
cout<<"终结符号如下: ";
cin>>terSymbol;
allSymbol = non_ter + terSymbol;
cout<<"文法产生式的个数: ";
cin>>n;
cout<<endl;
for(int i = 1;i <= n;i++){
cout<<"请输入第"<<i<<"产生式:"<<endl;
cin>>gramOldSet[i].formula;
}
cout<<"\n\n去除 | 之后的产生式:"<<endl;
initSet(gramOldSet,n);
for(int i = 0;i < n; i++){
cout<<gramOldSet[i].formula<<endl;
}
cout<<endl;
dealFIRSTVT();
dealLASTVT();
dealTable();
for(int i = 0;i<4;i++){
allContronl();
S.clear();
}
return 0;
}
2.写出上机调试时发现的问题,以及解决的过程;
(1)规约时,如果有连续的单个非终结符进行归约,那么会发现无法归约到指定的字符串,因为书本上的算法并没有指出应把所找到的最左素短语归约到哪一个非终结符‘N’。即算符优先一般不等价于规范归约。因此在进行归约的时候要根据前后符号的情况进行归约,判断要归约到那个非终结符,因此需要在归约过程中加入自身以及外界情况的的一些考量从而对代码进行修正。
3.写出你所使用的测试数据及结果;
测试数据:
ETF
+-*/()i
3
E→E+T|E-T|T
T→T*F|T/F|F
F→(E)|i
1+2
(1+2)/3+4-(5+6/7)
((1-2)/3+4
1+2-3+(*4/5)
4.谈谈你的体会。
由于算符优先分析并未对文法非终结符定义优先关系,所以就无法发现由单个非终结符组成的可规约串。也就是说,在算符优先归约过程中,我们无法用那些右部仅含一个非终结符的产生式(称为单非产生式,如P->Q)进行归约。(建议自行体会.jpg)
5.上机8小时,完成实验报告2小时。
实验报告