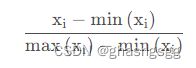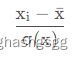标准化与归一化的简单介绍
标准化与归一化
无论标准化还是归一化都是针对某个特征(某一列)进行操作的
归一化
标准化
就是将训练集中某一列数值特征(假设是第i列)的值缩放成均值为0,方差为1的状态
归一化和标准化的相同点都是对某个特征(column)进行缩放(scaling)而不是对某个样本的特征向量(row)进行缩放。对特征向量进行缩放是毫无意义的(暗坑1) 比如三列特征:身高、体重、血压。每一条样本(row)就是三个这样的值,对这个row无论是进行标准化还是归一化都是好笑的,因为你不能将身高、体重和血压混到一起去!
在线性代数中,将一个向量除以向量的长度,也被称为标准化,不过这里的标准化是将向量变为长度为1的单位向量,它和我们这里的标准化不是一回事儿,不能搞混(暗坑2)
标准化/归一化的好处
提升模型精度
在机器学习算法的目标函数(例如 SVM 的 RBF 内核或线性模型的 L1 和 L2 正则化),许多学习算法中目标函数的基础都是假设所有的特征都是零均值并且具有同一阶数上的方差。如果某个特征的方差比其他特征大几个数量级,那么它就会在学习算法中占据主导位置,导致学习器并不能像我们说期望的那样,从其他特征中学习
经验上说,归一化是让不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性
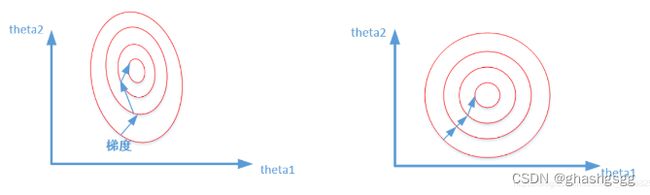
提升收敛速度
比较这两个图,前者是没有经过归一化的,在梯度下降的过程中,走的路径更加的曲折,而第二个图明显路径更加平缓,收敛速度更快。 对于神经网络模型,避免饱和是一个需要考虑的因素,通常参数的选择决定于 input 数据的大小范围
标准化/归一化的对比分析
首先明确,在机器学习中,标准化是更常用的手段,归一化的应用场景是有限的
标准化更好保持了样本间距
当样本中有异常点时,归一化有可能将正常的样本“挤”到一起去。比如三个样本,某个特征的值为1,2,10000,假设10000这个值是异常值,用归一化的方法后,正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的,那么,当我们用梯度下降来做分类模型训练时,模型会需要更长的时间收敛,因为将样本分开需要更大的努力!而标准化在这方面就做得很好,至少它不会将样本“挤到一起”。
标准化更符合统计学假设
对一个数值特征来说,很大可能它是服从正态分布的。标准化其实是基于这个隐含假设,只不过是略施小技,将这个正态分布调整为均值为0,方差为1的标准正态分布而已
逻辑回归必须要进行标准化吗
真正的答案是,这取决于我们的逻辑回归是不是用正则。
- 如果你不用正则,那么,标准化并不是必须的,
- 如果你用正则,那么标准化是必须的。
因为不用正则时,我们的损失函数只是仅仅在度量预测与真实的差距,加上正则后,我们的损失函数除了要度量上面的差距外,还要度量参数值是否足够小。而参数值的大小程度或者说大小的级别是与特征的数值范围相关的。举例来说,我们用体重预测身高,体重用kg衡量时,训练出的模型是:
身 高 = w ∗ 体 重 身高 = w * 体重
身高=w∗体重
w 就是我们训练出来的参数。
当我们的体重用吨来衡量时,w 的值就会扩大为原来的 1000 10001000 倍。
在上面两种情况下,都用 L1 正则的话,显然对模型的训练影响是不同的。
假如不同的特征的数值范围不一样,有的是0到0.1,有的是100到10000,那么,每个特征对应的参数大小级别也会不一样,在 L1 正则时,我们是简单将参数的绝对值相加,因为它们的大小级别不一样,就会导致 L1 最后只会对那些级别比较大的参数有作用,那些小的参数都被忽略了
标准化对 LR 的好处
进行标准化后,我们得出的参数值的大小可以反应出不同特征对样本label的贡献度,方便我们进行特征筛选。如果不做标准化,是不能这样来筛选特征的
标准化注意事项
最大的注意事项就是先拆分出 test 集,只在训练集上标准化, 即均值和标准差是从训练集中计算出来的,不要在整个数据集上做标准化,因为那样会将 test 集的信息引入到训练集中,这是一个非常容易犯的错误!
哪些模型需要标准化,哪些不需要
需要标准化的模型
线性回归,LR,Kmeans,KNN, SVM 等一些涉及到距离有关的算法,
聚类算法 PCA等
GBDT、adaboost
因为GBDT的树是在上一颗树的基础上通过梯度下降求解最优解,归一化能收敛的更快,GBDT通过减少bias来提高性能
1、一般算法如果本身受量纲影响较大,或者相关优化函数受量纲影响大,则需要进行特征归一化。
2、树模型特征归一化可能会降低模型的准确率,但是能够使模型更加平稳
不需要标准化的模型
也不是所有的模型都需要做归一的,比如模型算法里面没有关于对距离的衡量,没有关于对变量间标准差的衡量。比如 decision tree 决策树,他采用算法里面没有涉及到任何和距离等有关的,所以在做决策树模型时,通常是不需要将变量做标准化的。
概率模型不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、随机森林(RF)
时,通常是不需要将变量做标准化的。
概率模型不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、随机森林(RF)