机器学习入门笔记

机器学习笔记

sklearn中文文档

一. 使用scikit-learn导入数据集

1. pycharm解决到导入库的问题

1. 找到pycharm的终端Terminal
   
2. 输入命令行pip3 sklearn安装对应的包

2. 数据集简单描述

scikit-learn 包括一些标准数据集，不需要从外部下载，可直接导入使用，比如与分类问题相关的Iris数据集和digits手写图像数据集，与回归问题相关的波士顿房价数据集。
以下列举一些简单的数据集，括号内表示对应的问题是分类还是回归：

 #加载并返回波士顿房价数据集（回归）
load_boston([return_X_y])
#加载并返回iris数据集（分类）
load_iris([return_X_y])             
#加载并返回糖尿病数据集（回归）
load_diabetes([return_X_y])          
#加载并返回数字数据集（分类）
load_digits([n_class, return_X_y]) 
#加载并返回linnerud数据集（多分类）   
load_linnerud([return_X_y])      

这些标准数据集采用类字典的对象格式存储,比如.data表示原始数据，是一个(n_samples,n_features)二维数组，通过.shape可以得到二维数组大小，.target表示存储数据类别即标签。
下面我们将利用datasets加载数据集digits作为示例:

from sklearn import datasets
if __name__ == "__main__":
    digits = datasets.load_digits()
    x = digits.data
    y = digits.target
    print(x[:2])
    print(y[:10])
    print(x.shape)

结果

[[ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.
  15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.
   0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.
   0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]
 [ 0.  0.  0. 12. 13.  5.  0.  0.  0.  0.  0. 11. 16.  9.  0.  0.  0.  0.
   3. 15. 16.  6.  0.  0.  0.  7. 15. 16. 16.  2.  0.  0.  0.  0.  1. 16.
  16.  3.  0.  0.  0.  0.  1. 16. 16.  6.  0.  0.  0.  0.  1. 16. 16.  6.
   0.  0.  0.  0.  0. 11. 16. 10.  0.  0.]]
[0 1 2 3 4 5 6 7 8 9]
(1797, 64)

Process finished with exit code 0

• 原始数据集data是一个二维列表
• .target表示存储数据类别即标签是一个一维列表
• .shape是一个二元列表，存储行数和列数

二. 数据预处理 — 标准化

1. 为什么要预处理

原始数据总是比较杂乱、不规整的，直接加载至模型中训练，会影响预测效果。使用sklearn 对导入的数据进行预处理。
原始数据存在的几个问题：不一致、重复、含噪声、维度高。数据挖掘中，数据预处理包含数据清洗、数据集成、数据变换和数据归约几种方法

sklearn.preprocessing 模块提供很多公共的方法，将原始不规整的数据转化为更适合分类器的具有代表性的数据。一般说来，使用标准化后的数据集训练学习模型具有更好的效果。

数据标准化的方法有很多种，常用的有“最小—最大标准化”、“Z-score标准化”等等。经过上述标准化处理，各属性值都处于同一个数量级别上，可以进行综合数据分析。

2. 常用的处理方法

• Z-score 标准化
  这种方法基于原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。将 A 的原始值 x 使用 Z-score 标准化到 x’。
  Z-score 标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况，其公式为：
  新数据 =（原数据-均值）/标准差
  使用sklearn preprocessing.scale直接将给定数据进行标准化

from sklearn import datasets
from sklearn import preprocessing
import numpy as np
if __name__ == "__main__":
    x = np.array([[1., -1.,  2.],
                    [2., 0., 0.],
                    [0., 1., -1.]])
    x_scaled = preprocessing.scale(x)
    print(x_scaled)
    # 经过标准化处理后，数据的均值和方差
    print(x_scaled.mean(axis = 0))
    print(x_scaled.std(axis = 0))

打印的结果为

[[ 0.         -1.22474487  1.33630621]
 [ 1.22474487  0.         -0.26726124]
 [-1.22474487  1.22474487 -1.06904497]]
[0. 0. 0.]
[1. 1. 1.]

sklearn.preprocessing.StandardScaler类实现了 Transformer 接口，可以保存训练数据中的参数（均值 mean_、缩放比例 scale_），并能将其应用到测试数据的标准化转换中。

from sklearn import datasets
from sklearn import preprocessing
import numpy as np
if __name__ == "__main__":
    x = np.array([[1., -1.,  2.],
                    [2., 0., 0.],
                    [0., 1., -1.]])
    scaler = preprocessing.StandardScaler().fit(x)
    print("均值 = ", scaler.mean_, sep = ' ')
    print("缩放比例 = ", scaler.scale_, sep= ' ')
    print(scaler.transform(x))

结果为

均值 =  [1.         0.         0.33333333]
缩放比例 =  [0.81649658 0.81649658 1.24721913]
[[ 0.         -1.22474487  1.33630621]
 [ 1.22474487  0.         -0.26726124]
 [-1.22474487  1.22474487 -1.06904497]]

Process finished with exit code 0

测试的原数据为

([[1., -1.,  2.],
  [2., 0., 0.],
  [0., 1., -1.]])

而均值是[1. 0. 0.3333]，是按列来求取的均值

• min-max 标准化
  min-max 标准化方法是对原始数据进行线性变换。设 minA 和 maxA 分别为属性 A 的最小值和最大值，将 A 的一个原始值 x 通过 min-max 标准化，映射成在区间[0,1]中的值 x’，其公式为：
  新数据=（原数据-极小值）/（极大值-极小值）
  原始数据的值一定是介于[min, max] ，所以这个公式可以把所有的数映射到[0, 1]
  sklearn.preprocessing.MinMaxScaler将属性缩放到一个指定的最大和最小值（通常是1-0）之间。
  MinMaxScaler 中可以通过设置参数feature_range=(min, max)指定最大最小区间。其具体的计算公式为：

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min

这里X_std是新数据占的比例，X_scaled为新的数据。运营了区间重映射

from sklearn import datasets
from sklearn import preprocessing
import numpy as np
if __name__ == "__main__":
    x = np.array([[1., -1.,  2.],
                    [2., 0., 0.],
                    [0., 1., -1.]])
    min_max_scale = preprocessing.MinMaxScaler();
    x_train_minmax = min_max_scale.fit_transform(x)
    #以上两个语句等价于 x_train_minmax = preprocessing.MinMaxScaler().fit_transform(x)
    print(x_train_minmax)

测试结果为

[[0.5        0.         1.        ]
 [1.         0.5        0.33333333]
 [0.         1.         0.        ]]

3. numpy中抽取部分列

numpyAr[rowstart : rowend , [ x, y,.... ] ] 表示提取从[rowstart, rowend)的第x,y…列数据
例子

from sklearn import datasets
from sklearn import preprocessing
import numpy as np
if __name__ == "__main__":
    x = np.array([[1., -1.,  2.],
                    [2., 0., 0.],
                    [0., 1., -1.]])

    print(x[0:2, [0,2,0]])

提取x数组的0,1行的第0,2,0列
结果为

[[1. 2. 1.]
 [2. 0. 2.]]

三. 文本数据特征提取

标准化一般主要针对数值型数据。对于文本数据，我们无法直接将原始文本作为训练数据，需通过特征提取将其转化为特征向量。

1. 相关知识

文本分析是机器学习算法的一个主要应用领域。文本分析的原始数据无法直接输入算法，因为大部分算法期望的输入，是固定长度的数值特征向量，而不是可变长的文本数据。
为了解决这个问题，sklearn 提供了一些实用工具，用最常见的方式从文本内容中抽取数值特征。比如说：

• 分词（tokenizing），对句子分词后，为每一个词（token）分配的一个整型 id，通常用空格和标点符号作为分词的分割符；
• 计数（counting），计算某个词在文本中的出现频率；
• 归一化权重(nomalizating and weighting)， 降低在大多数样本/文档中都出现的词的权重。

在文本特征提取中，特征和样本的定义如下：将每个词出现的频率作为特征；将给定文档中所有词的出现频率所构成的向量看做一个样本。因此，整个语料库可以看做一个矩阵，矩阵的每行代表一个文档，每列代表一个分词。我们将文档集合转化为数值特征向量的过程称为向量化。这一整套策略被称为词袋模型，用词频描述文档，完全忽略词在文档中出现的相对位置信息。

2. sklearn中文本数据特征提取的方法

**CountVectorizer模块**实现了分词和计数，该方法包含许多参数，打印了其默认的参数值。

• 导入类
  from sklearn.feature_extraction.text import CountVectorizer
  也可以直接使用
  vectorizer = sklearn.feature_extraction.text.CountVectorizer()

• 查看默认值
  

常用默认值

• input : 指定输入格式；
• tokenizer : 指定分词器；
• stop_words : 指定停止词，比如当设置 stop_words="english"时，将会使用内建的英语停用词列表；
• max_df : 设置最大词频，若为浮点数且范围在[0,1]之间，则表示频率，若为整数则表示频数；
• min_df : 设置最小词频；
• max_features: 设置最大的特征数量；
• vocabulary: 指定语料库，即指定词和特征索引间的映射关系表。

属性:

• vocabulary_ : 字典类型，返回词和特征索引间的映射关系表；

#得到词汇映射表
vocab = vectorizer.vocabulary_
#字典结构，返回特征值‘document’对应的下标索引
vectorizer.vocabulary_.get('document')

• stop_words_ : set 集合，停止词集合。

方法:

• fit(raw_documents[, y]) : 从原文本数据得到词汇-特征索引间的映射关系CountVectorizer().vocabulary_；

import sklearn
from  sklearn.feature_extraction.text import CountVectorizer
if __name__ == "__main__":
    vectorizer = sklearn.feature_extraction.text.CountVectorizer()
    corpus = ["This is pen",
              "This is a book",
              "hello world"]
    x = vectorizer.fit(corpus)
    print(vectorizer.vocabulary_)

结果为

{'this': 4, 'is': 2, 'pen': 3, 'book': 0, 'hello': 1, 'world': 5}

• transform(raw_documents) :将原文本集合转换为特征矩阵；
• fit_transform(raw_documents[, y]): 结合 fit 和 transform 方法，返回特征矩阵，如下图所示：
  
• build_analyzer():返回预处理和分词的引用；
  下图表示对“This is a text document to analyze.”进行分词并验证结果。
  
• get_feature_names():返回特征索引id对应的特征名字（下标对应的某个词）；
  
  将向量化转换器应用到新的测试数据。
  

注意：transform函数的返回结果是一个矩阵（sparse matrix），为了更好的表示数据，采用toarray()将数据转化为 numpy 数组，注意接下来的编程任务中，也要转化为一个数组。

在文本语料库中，一些词非常常见（例如，英文中的“the”，“a”，“is”），但是有用信息含量不高。如果我们将词频直接输入分类器，那些频繁出现的词会掩盖那些很少出现，但是更有意义的词，将达不到比较好的预期效果。为了重新计算特征的计数权重，通常都会进行 TFIDF 转换。
TFIDF 的主要思想是：如果某个词或短语在一篇文章中出现的频率高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。TFIDF 实际上是：TF * IDF，TF 词频(Term Frequency)，IDF 反文档频率(Inverse Document Frequency)。TF 词频(Term Frequency)指的是某一个给定的词语在该文件中出现的次数。IDF 反文档频率(Inverse Document Frequency)是指如果包含词条的文档越少，IDF 越大，则说明词条具有很好的类别区分能力。

sklearn 中的 TfidfVectorizer 模块，实现了 TFIDF 思想。该模块的参数、属性及方法与 CountVectorizer 类似，可参考 CountVectorizer 的调用方式。

四. 采用 scikit-learn 中的 svm 模型，训练一个对 digits 数据集进行分类的模型。

1. 相关知识

在 scikit-learn 中，对于分类问题的估计器是一个实现了fit(X, y) 和predict(T)方法的 Python 对象。估计器的实例很多，例如实现了支持向量分类的类sklearn.svm.svc。估计器的结构可以通过初始化模型时设置的参数决定，但目前，我们将估计器看做一个黑盒子，先不关心具体的参数设置。
digits 数据集中包含大量的数字图片，如下图所示，我们希望给定其中的一张图片，能识别图中代表的数字，这是一个分类问题，数字 0…9 代表十个分类，目标是希望能正确估计图中样本属于哪一个数字类别。

digits 数据集可以通过以下命令导入:

from sklearn import datasets
digits = datasets.load_digits()

digits 的原始图像采用一个(8,8)的二维数组表示，如下图所示：可以通过digits.data查看图片数据表示，行表示样本数量，列表示样本特征（将(8,8)的矩阵压缩成一行，可以从digits.data.shape的列数为 64 维看出，）；digits.target给出 digits 数据集的真实值，即我们要学习的每个数字图像对应的数字。

import matplotlib.pyplot as plt

# 导入数据集，分类器相关包
from sklearn import datasets, svm, metrics

# 导入digits数据集
digits = datasets.load_digits()
n_samples = len(digits.data)
data = digits.data

# 使用前一半的数据集作为训练数据，后一半数据集作为测试数据
train_data,train_target = data[:n_samples // 2],digits.target[:n_samples // 2]
test_data,test_target = data[n_samples // 2:],digits.target[n_samples // 2:]


def createModelandPredict():
    '''
    创建分类模型并对测试数据预测

    返回值：
    predicted - 测试数据预测分类值
    '''
    predicted = None
    #   请在此添加实现代码   #
    #********** Begin *********#
    classifier = svm.SVC()
    classifier.fit(train_data, train_target)
    predicted = classifier.predict(test_data)
    
    #********** End **********#

    return predicted

五. 机器学习的常见术语

• 我们把数据中的每一行称为一个示例或样本；

• 反映事件或对象在某方面的表现或性质的事项，如：色泽、根蒂、敲声，称为属性或特征；

• 属性上的取值，例如：青绿、乌黑。称为属性值或特征值；

• 我们把一个示例（样本）称为一个特征向量。
  
  从数据中学得模型的过程称为“学习”或“训练”，这个过程通过执行某个学习算法来完成。训练过程中使用的数据称为“训练数据”，其中每个样本称为一个“训练样本”，训练样本组成的集合称为“训练集”，学习过程就是为了找出或逼近真相。

假设空间
假设空间在已知属性和属性可能取值的情况下，对所有可能满足目标的情况的一种毫无遗漏的假设集合。

接下来举个例子来说明什么是假设空间。在选择配偶时我们可能有以下几个指标：

• 体型 : 肥胖，匀称，过瘦；

• 财富 : 富有，一般，贫穷；

• 性子 : 急，不急不慢，慢。

现在我们要构建一个合适的假设空间来构建一个择偶观：

对于体型来说有肥胖、均匀和过瘦 3 种，也有可能价值观里认为这个无关紧要，所以有4种可能。

对于财富来说有富有、一般以及贫穷 3 种可能，也有可能价值观里认为这个无关紧要，所以有4种可能。

对于性子来说有急、不急不慢以及慢 3 种可能，也有可能价值观里认为这个无关紧要，所以有4种可能。

最后再加上一个极端的情况，也就是体型、财富以及性子这 3 个评判准则选出来的都不是想要的配偶。

所以假设空间的规模大小为444+1=65。

归纳偏好
归纳偏好是机器学习算法在学习过程中对某种类型假设的偏好。说白了就是“什么样的模型更好”这一问题。

以韦小宝的 7 个老婆为例，这 7 个老婆均满足小宝的要求，因此构成了大小为 7 的假设空间。(实际上，假设空间的大小一定是无穷大的。为了说明问题，我们暂时以 7 为大小)。那么，如何衡量哪一个假设空间中哪一个假设函数（老婆）最好呢？如果以温柔体贴为偏好来选，当然是小双；如果以小宝的迷恋为偏好来讲，假设函数就是阿珂。说白了，归纳偏好就是一个用于挑选假设函数的基准

因此归纳偏好可看作学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或“价值观”。

而在具体的现实问题中，学习算法本身所做的假设是否成立，也即算法的归纳偏好是否与问题本身匹配，大多数时候直接决定了算法能否取得好的性能。

六. 机器学习的主要任务

分类是机器学习的一项主要任务，主要是将实例数据划分到合适的分类中。

机器学习的另外一项任务是回归，主要是预测数值型的数据，比如通过数据值拟合曲线等。

分类和回归属于监督学习，这类算法必须知道预测什么，即目标变量的分类信息。与监督学习相对应的是无监督学习，此时数据没有类别信息，也不会给定目标值。在无监督学习中，将数据集合分成由类似的对象组成的多个类的过程称为“聚类”。

接下来，我们来看看，什么是分类、回归与聚类。

1. 分类

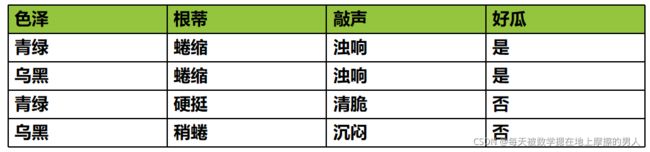
这是一系列关于西瓜的数据，这里的每个实体，或者每一行被称为一个样本或数据点，而每一列（用来描述这些实体的属性）则被称为特征。假如说，我们现在想通过色泽、根蒂、敲声这几个特征来区分一个西瓜是好瓜与不是好瓜，这就是一个分类问题。分类问题的目标是预测类别标签。在这个例子中，“是”与“否”则是预测类别的两个不同的标签。分类问题有时可分为二分类和多分类，西瓜的例子则是一个二分类问题，多分类指的是数据不止两个类别，它有多个类别。

2. 回归

回归任务的目标是预测一个连续值，编程术语叫作浮点数。假如说我们现在手里得到的是如下数据：

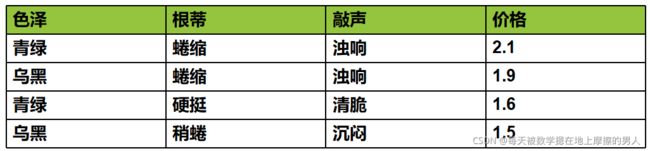
我们要通过色泽、根蒂、敲声来预测西瓜的价格，这就是一个回归问题。区分分类任务和回归任务有一个简单方法，就是看输出是否具有某种连续性。如果在可能的结果之间具有连续性，那么它就是一个回归问题，比如说价格。

3. 类聚

聚类属于无监督学习，它是指我们的数据只有输入，没有输出，并需要从这些数据中提取知识。聚类算法将数据划分成不同的组，每组包含相似的样本。比如说：
我们现在手里的数据只有色泽、根蒂、敲声这几个特征，我们通过这三个特征，把性状相似的西瓜分到一个组，这就是一个聚类问题。聚类问题与分类问题的本质区别就是有没有标签。