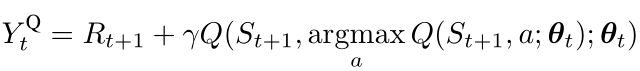Deep Reinforcement Learning with Double Q-learning（Double DQN）论文学习和公式推导

最近刚开始使用DQN，也会用DDQN，但是背后的原理不理解，所以读了这篇论文，下面以翻译并附带一些解释和公式推导的方式讲讲我个人的理解，有疑问可以多交流。

Abstract

Q-learning算法会在某些情况下存在对action values的过估计（overestimation）问题，但这种过估计是否普遍存在，是否影响性能，是否可避免，以前尚不清楚。作者在本文回答了这些问题，且证明了用于解决表格式问题（状态动作是一个一个离散的）的Double Q-learning算法背后的思想可以推广用于大规模函数逼近。作者提出了一种改进的DQN算法，减少了过估计现象。

 

Q-learning有时学到不切实际的高action value，原因是在估计action value时包含了max操作。以前的工作中，overestimation被归因于不够灵活的函数逼近（Thrun and Schwartz, 1993）和噪声（van Hasselt, 2010, 2011）。本文作者统一了这些观点，证明了当action value不准确时，无论逼近误差来源如何，都会产生overestimation问题。在实际学习过程中，不精确的价值估计是经常见到的，所以overestimation问题会经常出现。

overestimation是否会产生负面影响是未知的，但过度乐观的价值（overoptimistic value ）本身不一定是问题，如果所有value均匀地提高了，那每个动作的相对好坏并不会改变，对应的策略也不会受到影响。但是如果overestimation不是均匀产生，那它可能会对学习到的策略产生负面影响。

为了检验实践中overestimation是否大规模出现，作者研究了最新的DQN算法（Mnih et al., 2015）。从某种程度上讲（针对前面提到的逼近函数不够灵活和噪声），DQN的设计是最佳方案，因为神经网络提供了灵活的函数逼近功能，并且有较低的渐近逼近误差，同时环境（Atari 2600）的确定性也防止了噪声的影响。在即使在这样有利的条件下，DQN依然存在overestimation问题（这也就说明了前面Thrun and Schwartz和van Hasselt的观点都是片面的）。

本文证明了Double Q-Learning 算法背后的思想（最初在表格形式的环境中提出）可以推广到任意函数逼近，包括神经网络。将该思想应用到DQN上提出Double DQN，并证明了该算法不仅可以估计出更准确的value，而且在游戏中获得了更高的分数。这也反映出DQN中的overestimation确实导致policy变差，减少overestimation有益于学习到更好的policy。

 

Background

对于state和action数量过大的问题，由于参数量巨大，Q-learning无法学习到所有状态下所有动作的Q值，所以引入参数，用近似，以此来用少量的参数拟合实际的价值函数，公式（1）是参数的更新公式，公式（2）是目标的定义。

公式（1）和（2）的推导：

目标是确定参数以最小化近似函数和实际函数之前的均方误差（MSE），令均方误差为，

                                                                           

需要朝着梯度负方向调整来最小化，

                                                                            

是更新步长，可以理解为学习率，使用随机梯度进行更新来近似该期望（取一批样本计算平均值当作期望），

                                                                            

由于真实的价值函数是未知的，上述公式无法直接使用，因此需要找到真实价值函数的替代，使用的是作为替代，而基于的Q-learning进一步改进，用当前策略（greedy策略）去选择下一状态的动作，

                                     

上述推导结果就是论文里的公式（2），再用上述结果替代真实的，就得到了论文里的公式（1）。

 

Deep Q Network

对于DQN网络就是多层神经网络的参数，参数对于n维状态空间，包含m个动作的问题，DQN可以就相当于从到的映射函数，Mnih et al. (2015)等人提出的DQN有两个重要的部分，一是使用target network，另一个是experience replay。target network结构和policy network一样，参数为，每隔步将policy network的参数复制到target network，然后保持不变直到下次复制。target network用来估计目标，公式（2）里的目标就变为公式（3），

experience replay就是将观察到的状态转换样本存储起来，并随机均匀取样来更新网络参数。

 

Double Q-learning

在Q-learning和DQN的参数更新目标中（公式2和3），max操作使用相同的value来选择动作并评估动作，拿公式（2）举例子，公式中的选择是通过得到的，即令最大的；而选择后Q值的估算也是通过得到的，都使用了参数为的动作值函数Q，所以说动作的选择和评估使用了相同的value。而正是这个原因，使得overestimated value更容易被选择，从而导致overestimation。为了避免这种情况，将动作的选择和评估分离（decouple），这就是Double Q-learning的思想。具体的实现方法是：设置两个结构相同价值函数，每次将样本随机分配给某一个价值函数学习，从而学到两组权重，和,在每次更新时，一组权重用来确定贪婪策略（选择动作），另一组权重用于评估动作（计算Q值得到更新目标）。为了更清晰的比较，本文作者将公式（2）（Q-learning的目标）拆分重写为

Double Q-learning的目标可以表示为公式（4），

其实这个拆分在上面的推导过程中已经用到了，这里应该很好理解了，Q-learning中动作的选择和评估都是使用的权重，而Double Q-learning中动作的选择和评估分别使用了权重和。

 

Overoptimism due to estimation errors

Q-learning的overestimation问题首先由Thrun and Schwartz (1993)研究，他们发现如果action value包含在内均匀分布的随机误差，则每个目标被过估计到，是动作数量。此外，Thrun and Schwartz给出了一个具体的示例，其中这些overestimation甚至导致了此优策略，并在使用函数逼近的测试问题中显示了overestimation。后来，van Hasselt (2010) 提出，即使使用表格表示形式，环境中的噪声也可能导致overestimation，并提出了Double Q-learning。

作者将在本节证明，无论是环境噪声，函数逼近，不稳定，还是其他来源，任何类型的估计误差都可能导致向上偏差（upward bias）。在实践中，由于真实值是未知的，任何方法都会在学习过程中产生一些不准确的地方。上面提到的Thrun and Schwartz（1993）的结果给出了特定设置下Q-learning的overestimation上限，还需要进一步推导出Q-learning的overestimation下限。

作者给出了定理1，这里大概解释一下：在状态s下所有最优action value都相等，即对任意动作a，，也就是说s状态下最优Q值与动作无关。令是的无偏估计，，平均误差为0但不是每个动作的Q值误差都为0，，m是状态s下可执行动作数量,。在上述条件下，，这就是Q-learning的tight下限（不等式能放缩次数越多，不等式越松弛，作者也证明了这个不等式是tight）。在相同的条件下，Double Q-learning估计的绝对误差下限为0。

证明：记动作a的Q值的绝对误差为，每个动作的误差构成一个集合，假设。中的正误差记为，大小为，严格负误差记为，大小为（注意作者用了positive和strictly negative，也就是说在正误差集合里可以取到0，负误差集合里不能取到0）。

如果n=m，即没有负的误差，已知平均绝对误差，且绝对误差都非负，所以所有的都必须取0。而条件中已经说了不是每个误差都为0，，此时就与条件矛盾，所以。由于，且，可以推出，个绝对值加起来小于，那么单个绝对值的最大值一定小于，即，然后有

                                                                

此时可以推出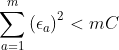（这一步中间过程论文里有我就省略了），然而推出的这个结果与条件矛盾。此时在假设下，无论还是都不成立，所以这个该假设不成立，即。当

时（取到下限），满足条件和，也就是说这个不等式不能再放缩了，即下限是tight的。

以上是Q-learning的overestimation下限推导，而Double Q-learning的overestimation下限，

证明：取和，满足定理1中的假设条件和，此时只需那么误差就是0，因为的Q值最大所以argmax操作取出，所以只需令，其他可以取任意值，只要保证通过Q函数取出来的的价值估计是正确的，误差就是0。

其实推导完也就懂了为什么Double Q-learning能够减少overestimation，就是在评估动作时使用了新的函数，不受已知条件限制。

定理1也表明，即使价值评估平均误差为0，任何来源的误差都会造成评估最大价值高于真实最优价值。根据定理1中的结论，Q-learning的，虽然随着动作数的增大下限减小，但这仅仅代表的是下限，真正取到下限是要满足特定条件的，而实际操作中，随着的增大，overestimation整体上在不断增加。

作者也给出了实验证明，上图中横坐标为动作数，纵坐标为估计的Q值与最优值的误差（重复100次取平均），橙色为Q-learning，蓝色为Double Q-learning，可以看出随着动作数增加，Q-learning误差逐渐增大，而Double Q-learning基本无偏。

证明了Double Q-learning能够减少overestimation后，现在将其应用到函数逼近上。作者做了三组实验，分别对应上图中三行图片，第一行，后两行，状态在上连续取值，每个状态下有10个离散的动作，为简单起见，真实的最优Q值仅取决于状态，也就是在每个状态下所有动作均有相同的真实最优Q值。

先分析左边的三行图，紫色的线代表每个状态真实的最优Q值，绿线为状态s下单个动作Q值的估计，绿点为采样点，直接从真实数据中采样，不含噪声，也就是样本中的Q值就是实际最优的Q值。总共有10个动作，每个动作仅仅在13个采样点中的11上采样，这样在未采样的点上可以更好反映函数逼近的效果，实际中也常会遇到这样的样本数据不足的问题。第一行和第二行实验使用6阶多项式去拟合，第三行实验使用9阶多项式。可以看出左图第二行在采样点上的逼近也不精确，是由于多项式阶数低不够灵活；左图第三行可以看出，虽然在采样点上逼近都很好，但在未采样的的地方误差很大，应该是过拟合了。

再看中间三行图，每幅图中10条绿线是10个动作分别对应的动作值函数，黑色虚线是每个状态下最大动作值。可以看出最大动作值基本都比左边图中的真实最优Q值大，也就是出现了overestimation。

最后看右边三行图，橙线是中间图中黑色虚线与左边图中紫线作差的结果，即，蓝线是使用了Double Q-learning的估计效果，蓝线的平均值更接近0，这表明Double Q-learning确实可以减少Q-learning在函数逼近中的overestimation问题。

通过实验，发现不够灵活的函数逼近对Q值的估计不精确，但是足够灵活的函数逼近在未知状态中会产生更大误差，导致更高的overestimation，DQN就是一种非常灵活的函数逼近，使用了神经网络来逼近价值函数。而overestimation最终会阻止学习到最优策略，作者后面也通过Atari上的实验证明了这点，且通过Double Q-learning减少overestimation最终策略也会得到改善。

 

Double DQN

Double DQN思想就是将目标中的max操作分解为使用不同的网络来进行动作选择和动作评估，以此来减少overestimation。而DQN中本来就使用了policy network和target network两个网络，所以无需再引入新的网络，只需改进DQN算法中的目标设计，即将公式（3）中的目标改为下面公式中的目标，

target network的更新方式并不改变，仍然是每隔固定步数从policy network复制。后面一部分就是作者做的DQN和Double DQN的对比实验了，比较简单易懂这里就不赘述了，里面倒是有一句话我很喜欢：“Good solutions must therefore rely heavily on the learning algorithm — it is not practically feasible to overfit the domain by relying only on tuning.”

 

Discussion

本文共有五个贡献。首先说明了为什么Q-learning会出现overestimation。其次通过实验分析，证明了overestimation在实践中比以前认识到的更加普遍和严重。第三，证明了可以通过Double Q-learning减少overestimation，使学习更稳定可靠。第四，基于DQN提出了Double DQN，无需新的网络结构或参数。最后证明Double DQN可以学习到更好的策略，在Atari 2600上获得state-of-the-art结果。