基于R语言的Lasso回归在水稻全基因组预测中的应用

基于R语言的Lasso回归在水稻全基因组预测中的应用

0 引言

全基因组选择是 21 世纪动植物育种的一种重要的选择策略，其核心就是全基因组预测，即基于分布在整个基因组上的多样性分子标记来对育种值进行预测，为个体的选择提供依据。

全基因组选择( genomic selection，GS) 是利用分布在整个基因组上的分子标记来估算育种值的一种高效、经济的方法．它实质上是估计所有基因或染色体片段的联合效应，并结合这些效应来预测基因组 估计的育种值( genomic estimated breeding value，GEBV)。

许多统计方法都可用于全基因组选择，包括贝叶斯方法( 贝叶斯 B) ，最佳线性无偏预测( BLUP) ， 以及正则化线性模型( 岭回归、Lasso 回归和弹性网络) 等。但是对于预测农作物的性状而言没有一种方法是完美的，它们各有各的特点，而预测的效果取决于模型的性质与性状的特点和遗传结构。

本文基于R语言编写Lasso回归方法对水稻产量和产量相关性状进行全基因组预测分析。

1 材料与方法

1.1 实验数据

水稻的产量（yd)等形状的数据来自胡老师在qq群的分享，其最初来源是Gains in QTL detection using an ultra-high density SNP map based on population sequencing relative to traditional RFLP/SSR markers. 实验人员实验人员将珍汕 97 A 和明恢 63 两个水稻品种作为亲本，杂交产生 210 个重组自交系( recombinant inbred lines，RIL) ，从这些重组自交系中收集 4 个产量相关性状的表型数据，它们分别是水稻产量( yd) ，千粒重( kgw) ，分蘖数( tp) 和单株谷粒数 ( gn) 。将各个重复的性状的平均表型值作为响应变量。基因组数据由水稻基因组的约270 000 个 SNP 推断的 1 619 个组( bin) 表示。组内的所有 SNP 都具有完全相同的分离模式( 完全的连锁不平衡( LD) ) ，因 此来自一组的一个SNP 足以代表整个组。210 个RIL 的基因型编码为: 1 代表珍汕97 A 基因型，0代表明 恢 63 基因型。

1.2 统计模型

1.2.1 Lasso 回归

在全基因组选择中，预测变量的数目( p) 通常远远大于个体的数目( n) 。在这种情况 下，普通最小二乘法( ordinary least-squares，OLS) 的估计值具有很差的预测能力，因为标记效应被视为固 定效应，这导致预测变量之间的多重共线性和过度拟合，从而使该模型不可行。

Lasso( least absolute shrinkage and selection operator) 是统计学家 Robert Tibshirani 在 1996 年提出的一种变量选择方法，它是 OLS 的约束版本，是一种基于线性回归模型的降维方法，对高维小样本数据的 稀疏模型十分有用，在基因表达谱分析中被广泛应用。Lasso 回归模型将任意选择一个并分解，而忽略其他 Lasso 模型，这使得 Lasso 的惩罚期望许多系数接近零．该方法也广泛应用于具有大量数据集的领域，例如基因组学。

2 模型代码详解

# 导入数据
load("D:\\生信数学基础\\G.Rdata")
load("D:\\生信数学基础\\RIL.Phe.Rdata")
# G
# 查看数据
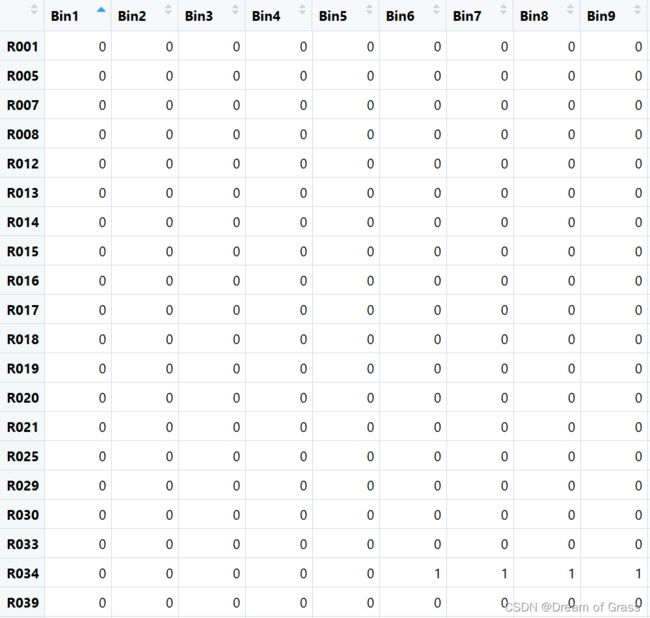
View(G)
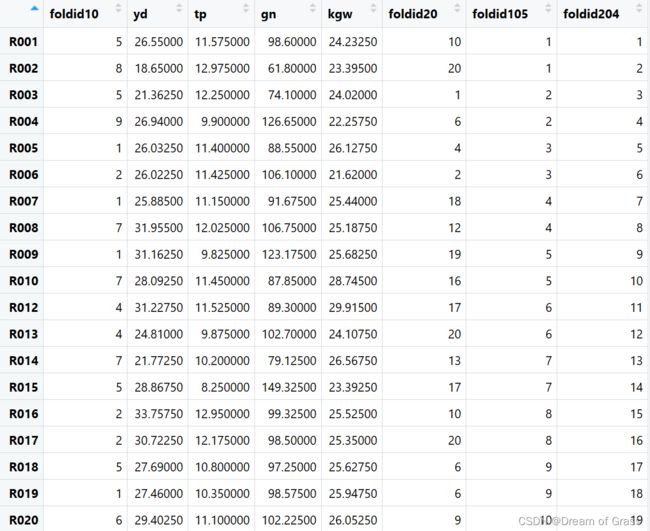
View(RIL.Phe)
dim(RIL.Phe)
# 210   8
dim(G)
# 210 1619

​ 图1. View(G)

​ 图2. View(RIL.Phe)

# 把X和Y放到一起
Gen$YD <- Phe$yd
dim(Gen)
# 210 1620
# 前面1619列是基因的数据，第1620列是水稻产量
sum(is.na(Gen))
# 没有缺失值，很好
# 把x和y给创建好
x <- model.matrix(YD~.,Gen)
# 除了产量
y <- Gen$YD

建造训练集和测试集

set.seed(6)
# 让别人用同样的随机种子能得到相同的结果
train <- sample(1:nrow(x),nrow(x)*7/10)
test <- (-train)
x.train <- x[train,]
dim(x.train)
# 147 1620
x.test <- x[test,]
dim(x.test)
# 63 1620
y.train <- y[train]
y.test <- y[test]
length(y.train)
# 147
length(y.test)
# 63
# 通过查看训练集和测试集的大小，发现没什么问题

导入相关库，并手动筛选$\lambda$

# 导入相关库
library(Matrix)
library(glmnet)
library(foreach)
grid <- 10^seq(10,-2,length=100)
# 100个数，都是10的多少次方，幂为10到-2中间100个数
LASSO.model <- glmnet(x.train,y.train,lambda = grid)
# 从grid中选候选lambda
str(LASSO.model)
coef(LASSO.model)[,70]
# 看到第70组的系数，发现几乎所有的系数都为0
# 下面我们来自己手工筛选一下
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[70])
sqrt(mean((LASSO.pred-y.test)^2))
# R2: 0.001134382
# RMSE: 4.568299
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[99])
mean((LASSO.pred-y.test)^2)
# R2: 0.001134382
# RMSE: 5.332769
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[90])
mean((LASSO.pred-y.test)^2)
# R2: 0.4626227
# RMSE: 4.55574
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[94])
mean((LASSO.pred-y.test)^2)
# R2: 0.8961105
# RMSE: 5.027624

下面用模型来筛选出最好的$\lambda$

cv.LASSO.model <- cv.glmnet(x.train,y.train,nfolds = 5)
str(cv.LASSO.model)
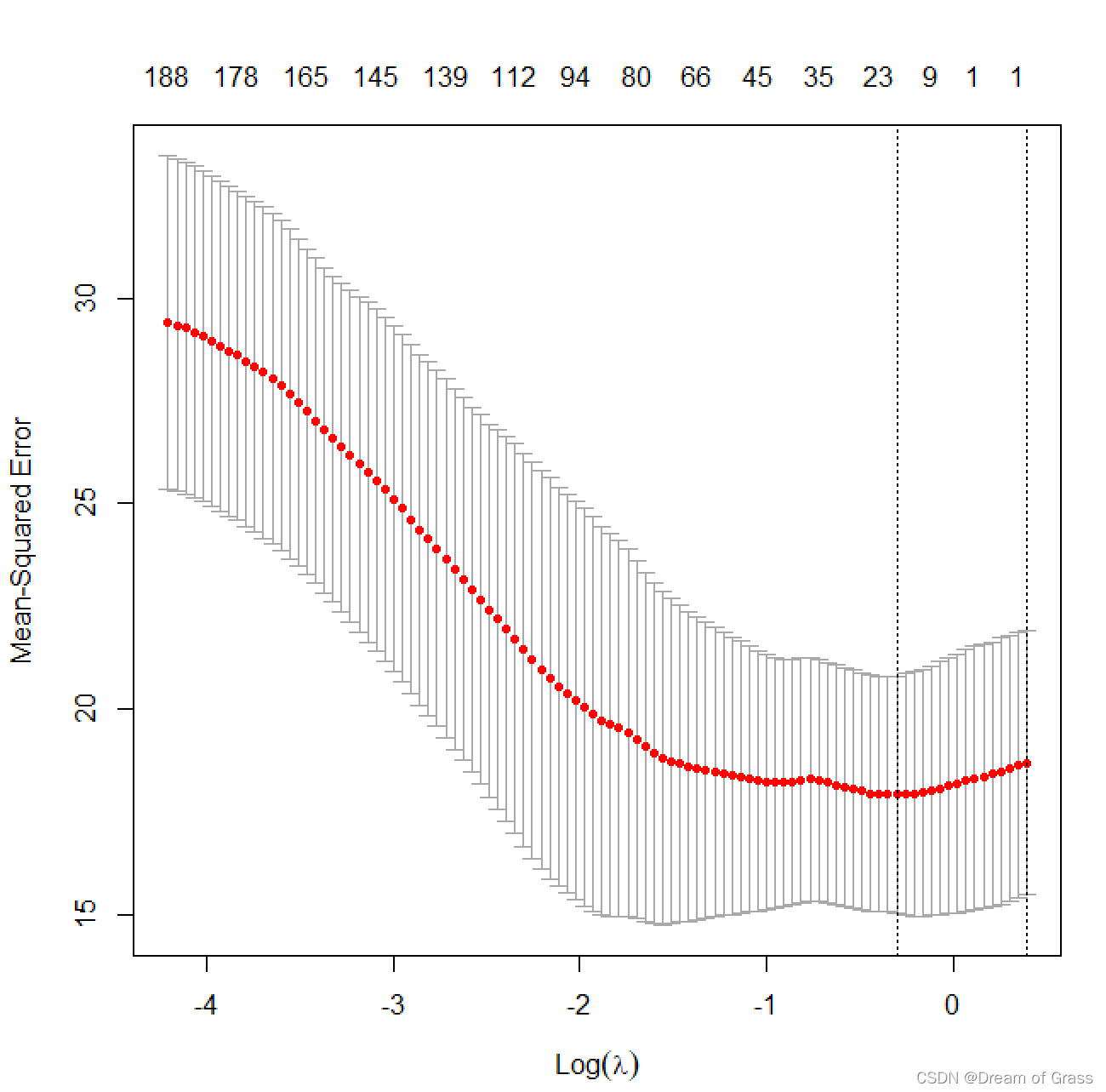
plot(cv.LASSO.model)
cv.LASSO.model$lambda.min
log(cv.LASSO.model$lambda.min)
cv.LASSO.pred <- predict(cv.LASSO.model,newx = x.test,s=cv.LASSO.model$lambda.min)
RMSE <- sqrt(mean((cv.LASSO.pred-y.test)^2))
RMSE
mean((cv.LASSO.pred-y.test)^2)
sum((cv.LASSO.pred-y.test)^2)
SSR <- sum((cv.LASSO.pred-mean(y.test))^2)
SSR
SST <- sum((y.test-mean(y.test))^2)
SST
R2 <- SSR/SST
R2

​ 图3. plot(cv.LASSO.model)

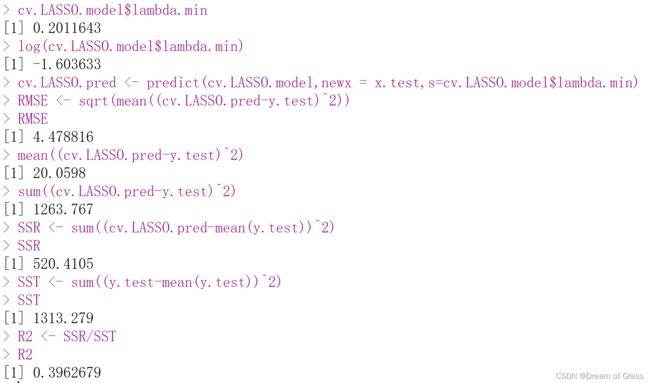
​ 图4. 程序输出结果

3 结果与分析

${\lambda }_{min}$	$RMSE$	$R^2$
0.2012	4.4788	0.3927

​ 表1. 输出结果（RMASE表示Root Mean Square Error,均方根误差）

所以由模型给出的结果是当$\lambda$=0.2012的时候，预测效果最好，$RMSE$在所进行的实验中也是最小的。

不过有意思的是，在之前手动取最小值的时候，偶然发现当$\lambda =0.0534$时，拟合优度$R^2$达到了0.89！

​
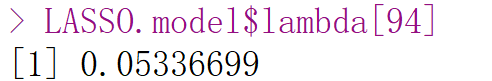
图5、6 偶然发现的好参数

然后我就把此时$\lambda$的取值放到$cv.LASSO.model$中，算出来的结果如下：

cv.LASSO.pred <- predict(cv.LASSO.model,newx = x.test,s=cv.LASSO.model$lambda.min)
cv.LASSO.pred <- predict(cv.LASSO.model,newx = x.test,s=0.05336699)
RMSE <- sqrt(mean((cv.LASSO.pred-y.test)^2))
RMSE
mean((cv.LASSO.pred-y.test)^2)
sum((cv.LASSO.pred-y.test)^2)
SSR <- sum((cv.LASSO.pred-mean(y.test))^2)
SSR
SST <- sum((y.test-mean(y.test))^2)
SST
R2 <- SSR/SST
R2

${\lambda }_{min}$	$RMSE$	$R^2$
0.05337	5.0851	0.9236

​ 表2. 有意思参数的输出结果

​ 图7. 有意思参数的输出结果

不过，模型给出的$\lambda$在$RMSE$ 评价指标中还是在所有实验中排在榜首的，说明模型还是很不错的！

4 附录

完整代码如下：

# 导入数据
load("D:\\生信数学基础\\G.Rdata")
load("D:\\生信数学基础\\RIL.Phe.Rdata")
# G
# 查看数据
fix(G)
fix(RIL.Phe)
typeof(RIL.Phe)
dim(RIL.Phe)
dim(G)
Phe <- as.data.frame(RIL.Phe)
Phe$yd
typeof(Phe)
Gen <- as.data.frame(G)
typeof(Gen)
# ?as.data.frame
# fix(Gen)
# 把X和Y放到一起
Gen$YD <- Phe$yd
# Gen$YD-Phe$yd
dim(Gen)
# 前面1619列是基因的数据，第1620列是水稻产量
sum(is.na(Gen))
# 没有缺失值，很好
# 把x和y给创建好
x <- model.matrix(YD~.,Gen)
# 除了产量
y <- Gen$YD
# fix(y)
# typeof(y)
set.seed(6)
# 让别人用同样的随机种子能得到相同的结果
# nrow(x)
train <- sample(1:nrow(x),nrow(x)*7/10)
# fix(train)
# train
test <- (-train)
# test
x.train <- x[train,]
# x.train
dim(x.train)
x.test <- x[test,]
dim(x.test)
y.train <- y[train]
y.test <- y[test]
length(y)
length(y.train)
length(y.test)
# 通过查看训练集和测试集的大小，发现没什么问题
# 导入相关库
library(Matrix)
library(glmnet)
library(foreach)
grid <- 10^seq(10,-2,length=100)
# 100个数，都是10的多少次方，幂为10到-2中间100个数
LASSO.model <- glmnet(x.train,y.train,lambda = grid)
# 从grid中选候选lambda
# LASSO.model
str(LASSO.model)
coef(LASSO.model)[,70]
# 看到第70组的系数，发现几乎所有的系数都为0
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[70])
# LASSO.pred
# y.test
SST <- sum((y.test-mean(y.test))^2)
SSR <- sum((LASSO.pred-mean(y.test))^2)
R2 <- SSR/SST
R2
sqrt(mean((LASSO.pred-y.test)^2))
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[99])
# LASSO.pred
# y.test
# LASSO.pred1-LASSO.pred3
SSR <- sum((LASSO.pred-mean(y.test))^2)
R2 <- SSR/SST
R2
mean((LASSO.pred-y.test)^2)
sqrt(mean((LASSO.pred-y.test)^2))
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[90])
# LASSO.pred
# y.test
SSR <- sum((LASSO.pred-mean(y.test))^2)
R2 <- SSR/SST
R2
mean((LASSO.pred-y.test)^2)
sqrt(mean((LASSO.pred-y.test)^2))
LASSO.pred <- predict(LASSO.model,newx = x.test,s=LASSO.model$lambda[94])
SSR <- sum((LASSO.pred-mean(y.test))^2)
R2 <- SSR/SST
R2
sqrt(mean((LASSO.pred-y.test)^2))
mean((LASSO.pred-y.test)^2)
LASSO.model$lambda[94]

cv.LASSO.model <- cv.glmnet(x.train,y.train,nfolds = 5)
str(cv.LASSO.model)
plot(cv.LASSO.model)
cv.LASSO.model$lambda.min
log(cv.LASSO.model$lambda.min)
cv.LASSO.pred <- predict(cv.LASSO.model,newx = x.test,s=cv.LASSO.model$lambda.min)
cv.LASSO.pred <- predict(cv.LASSO.model,newx = x.test,s=0.05336699)
RMSE <- sqrt(mean((cv.LASSO.pred-y.test)^2))
RMSE
mean((cv.LASSO.pred-y.test)^2)
sum((cv.LASSO.pred-y.test)^2)
SSR <- sum((cv.LASSO.pred-mean(y.test))^2)
SSR
SST <- sum((y.test-mean(y.test))^2)
SST
R2 <- SSR/SST
R2