一文搞懂时间序列预测模型（2）：ARIMA模型的理论与实践

本文通过一段时间的长江流量数据集来实战演示ARIMA模型的理论、建模及调参选择过程，其中包括数据准备、随机性、稳定性检验。本文旨在通过实践的操作过程，完成ARIMA模型的分享，相信大家也会通过此文而有所收获。

ARIMA的建模过程

1，对时间序列数据绘图，观察是否为平稳时间序列。
2，若时间序列数据是平稳时间序列，则直接进行下一步，若不是平稳时间序列，则对数据进行差分，转化为平稳时间序列数据。
3，对平稳时间学列数据绘制自相关系数ACF和偏自相关系数PACF图，通过对自相关图和偏自相关图分析，获得AM参数和AR参数。

ARIMA模型介绍

ARIMA模型是一种流行且广泛使用的时间序列预测统计方法。
ARIMA 是代表（Autoregressive Integrated Moving Average model ）差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），是时间序列预测分析方法之一。ARIMA(p，d，q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。

一般概念-时间序列平稳性

从统计学的角度来看，平稳性是指数据的分布在时间上平移时不发生变化。因此，非平稳数据显示了由于趋势而产生的波动，必须对其进行转换才能进行分析。例如，季节性会导致数据的波动，并可以通过“季节性差异”过程消除。

白噪声

白噪声是由一组0均值，不变方差，相互独立的元素构成，当然可以对该元素的分布进行假设(如高斯分布)。白噪声如同他的名字听起来一样是杂乱无章的，各元素之间没有任何联系。由白噪声组成的序列是随机游走，随机游走序列的自相关特点是其自相关函数几乎为1并且衰减很慢，这种特征我们称为长记忆性。

白噪声表示数据之间没有相关性，如果时间序列都是由白噪声数据构成的，那么时间序列的数据就不能是自相关的。

自回归模型AR

自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。

自回归模型首先需要确定一个阶数p，表示用几期的历史值来预测当前值。p阶自回归模型的公式定义为：

上式中yt是当前值,u是常数项,p是阶数 ri是自相关系数,et是误差。

自回归模型有很多的限制：

1、自回归模型是用自身的数据进行预测
2、时间序列数据必须具有平稳性
3、自回归只适用于预测与自身前期相关的现象

移动平均模型MA

移动平均模型关注的是自回归模型中的误差项的累加 ，q阶自回归过程的公式定义如下：

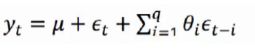
移动平均法能有效地消除预测中的随机波动。

差分法 I

对于非平稳序列可以使用差分法使得数据更平稳，常用的方法有一阶差分和二阶差分法。一阶差分公式：

自回归移动平均模型ARMA

自回归模型AR和移动平均模型MA模型相结合，就得到了自回归移动平均模型ARMA(p,q)，计算公式如下：

差分自回归移动平均模型ARIMA

将自回归模型、移动平均模型和差分法结合，我们就得到了差分自回归移动平均模型ARIMA(p,d,q)，其中d是需要对数据进行差分的阶数。

ARIMA实战

ARIMA的一般步骤

1，对时间序列数据进行绘图，检验数据的平稳性，对非平稳时间序列数据，要先进行差分，直到时间序列为平稳时间序列。
2，对平稳后的数据进行白噪声检验，白噪声是指零均值常方差的随机平稳序列。
3，如果是平稳非白噪声序列就计算ACF（自相关系数）、PACF（偏自相关系数），进行ARIMA模型识别。
4，对识别好的模型，确定模型参数，进行时间序列进行预测，并对模型结果进行评价。

Python 实现ARIMA模型

1、导入必要的函数库

import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math
 
from pandas.plotting import autocorrelation_plot
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.preprocessing import MinMaxScaler

from IPython.display import Image
 
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf  
from statsmodels.tsa.stattools import adfuller  # adf检验库
from statsmodels.stats.diagnostic import acorr_ljungbox  # 随机性检验库
from statsmodels.tsa.arima_model import ARMA 
 
%matplotlib inline
plt.rcParams['figure.figsize'] = (12,6)
pd.options.display.float_format = '{:,.2f}'.format
np.set_printoptions(precision=2)
warnings.filterwarnings("ignore") # specify to ignore warning messages

2、导入数据

flow_data=pd.read_csv(r".k\data\TimeSeries\monthly-flows-chang-jiang-at-hankou.csv")
flow_data.head(3)

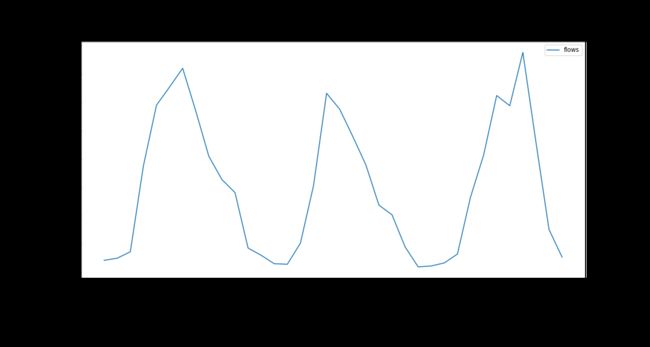
绘制从1975年至1978年（选择时间的窗口较短，主要便于观察数据的变化）汉口所测长江流量数据。通过这些数据可以观察数据的平稳性。

flow_data[-36:].plot(y='flows',x="month", subplots=True, 
            figsize=(15, 8), fontsize=12)
plt.xlabel('month', fontsize=12)
plt.ylabel('flows', fontsize=12)
plt.show()

3、划分测试集和训练集

现在已经对数据进行了导入，并对数据的平稳性进行了可视化分析，通过分析我们可以发现，分析的该数据是平稳序列数据。

通常，需要将数据集划分为训练集和测试集，一般在训练集上完成对模型的训练，当完成模型的训练后，使用测试集来评估模型的准确性。为了确保模型测试的准确性，需要时间序列的测试集数据早于且不包含测试集的数据。

将模型的数据划分为两段，其中，1978年1月之后的数据为测试集，1978年之前的数据为训练集。

train_start_dt = '1865-01'
test_start_dt = '1978-01'

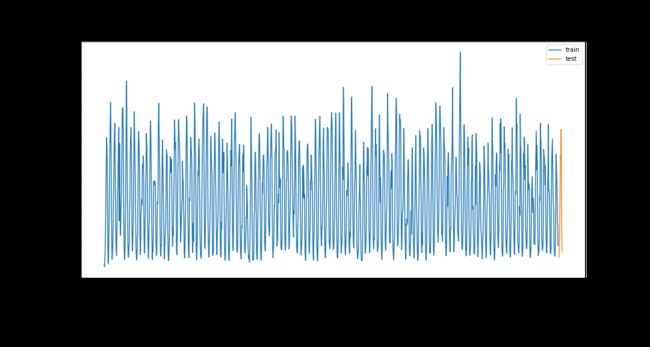
4、可视化预测集和测试集数据差异

为了更加直观地看出训练集和测试集的差异，我们在同一张图中用不同颜色区分两个测试集，蓝色为训练集、橙色为测试集。

flow_data[(flow_data["month"] < test_start_dt)][['flows']].rename(columns={'flows':'train'}) \
    .join(flow_data[(flow_data["month"] > test_start_dt)][['flows']].rename(columns={'flows':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('flow', fontsize=12)
plt.show()

稳定性检验

adfuller(Augmented Dickey-Fuller)测试可用于在存在串行相关的情况下在单变量过程中测试单位根。

statsmodels.tsa.stattools.adfuller(x，
maxlag = None，regression ='c'，autolag ='AIC'，
store = False，regresults = False )

adfuller中可进行adf校验，一般传入一个data就行，包括 list, numpy array 和 pandas series都可以作为输入，其他参数可以保留默认。

如何确定时间序列的平稳性？主要看：

1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较，ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设。另外，P-value是否非常接近0，接近0，则是平稳的，否则，不平稳。

若不平稳，则需要进行差分，差分后再进行检测。

def adf_val(ts, ts_title):
    '''
    ts: 时间序列数据，Series类型
    ts_title: 时间序列图的标题名称，字符串
    author:zhongzhi
    '''     
    # 稳定性（ADF）检验
    adf, pvalue, usedlag, nobs, critical_values, icbest = adfuller(ts)  
 
    name = ['adf', 'pvalue', 'usedlag',
            'nobs', 'critical_values', 'icbest']    
    values = [adf, pvalue, usedlag, nobs, 
              critical_values, icbest]  
    print(list(zip(name, values)))
 
    return adf, pvalue, critical_values,  
    # 返回adf值、adf的p值、三种状态的检验值

利用上面所定义的函数，对数据进行平稳性检验。

ts_data = flow_data['flows'].astype('float32')  
adf, pvalue1, critical_values = adf_val(
          ts_data, 'raw time series')

acf结果为-5.49 小于3个value的值，p_value也接近与0，所以是平稳的

白噪声检验

白噪声检验也称为纯随机性检验，当数据是纯随机数据时，再对数据进行分析就没有任何意义了，所以拿到数据后最好对数据进行一个纯随机性检验。

# 数据的纯随机性检验函数
acorr_ljungbox(x, lags=None, boxpierce=False, 
               model_df=0, period=None, 
               return_df=True, auto_lag=False)

构建随机性检验函数

def acorr_val(ts):
    '''
    # 白噪声（随机性）检验
    ts: 时间序列数据，Series类型
    返回白噪声检验的P值
    '''
    lbvalue, pvalue = acorr_ljungbox(ts, lags=1)  # 白噪声检验结果
    return lbvalue, pvalue
    
acorr_val(ts_data)

(array([905.15]), array([7.45e-199]))

搭建ARIMA模型

可以使用python 的statsmodels 库创建 ARIMA 模型。并遵循以下几个步骤。

1、通过调用SARIMAX()并传入模型参数： p, d, q参数，以及 P, D, Q参数定义模型。

2、通过调用fit()函数为训练数据准备模型。

3、通过调用forecast()函数进行预测，并指定要预测的步骤数(horizon)。

在ARIMA模型中，有3个参数用于帮助对时间序列的主要方面进行建模：季节性、趋势和噪声。

p：与模型的自回归方面相关的参数，模型中包含的滞后观测数，也称为滞后阶数。
d：与模型集成部分相关的参数，原始观测值差异的次数，也称为差异度。它影响到应用于时间序列的差分的数量。
q：与模型的移动平均部分相关的参数。移动平均窗口的大小，也称为移动平均的阶数。

值 0 可用于参数，表示不使用模型的该元素。这样，ARIMA 模型可以配置为执行 ARMA 模型的功能，甚至是简单的 AR、I 或 MA 模型。

通过上图的数据分析发现，我们发现相关数据具有较强的季节性。下面我们需要确定数据的季节性周期。

原始数据使用ACF函数，会绘图：

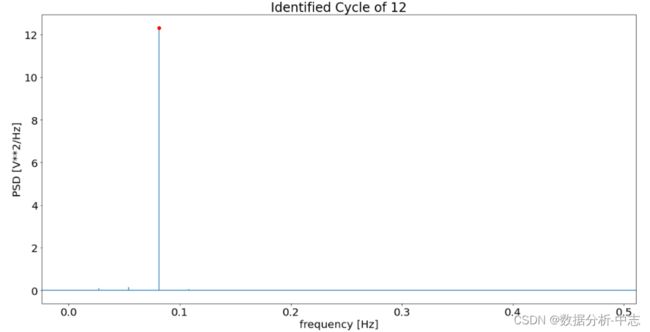
从图中可以看到，该图可以很明显的识别季节的周期为12个月，因此，我们需要每隔12个月间隔的差分来消除季节性，然后对消除掉季节性的数据继续分析其平稳性、ACF、PACF函数特性，从而确定ARIMA模型。

# test stationarity after removing seasonality
Seasonality=12
waterFlowS12 = train.diff(Seasonality)[Seasonality:]
print("ADF test result shows test statistic is %f and p-value is %f" %(adftestS12[:2]))

nlag=36
xvalues = np.arange(nlag+1)

acfS12, confiS12 = sm.tsa.stattools.acf(waterFlowS12, nlags=nlag, alpha=0.05, fft=False)
confiS12 = confiS12 - confiS12.mean(1)[:,None]

fig = plt.figure()
ax0 = fig.add_subplot(221)
waterFlowS12.plot(ax=ax0)

ax1=fig.add_subplot(222)
sm.graphics.tsa.plot_acf(waterFlowS12, lags=nlag, ax=ax1)
plt.show()

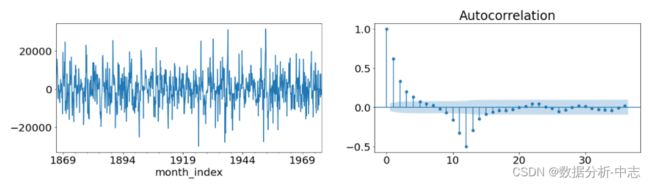
如图所示，去掉季节性的数据图像显示这个时间序列有非常强的均值回归行为，ACF图显示为逐渐递减的序列直到第12个滞后项，但是第12个滞后项都没有显著的数值，这两点说明，去掉季节性的操作是比较成功的，但是还需要进行1阶差分。

# test stationarity after removing seasonality

waterFlowS12d1 = waterFlowS12.diff(1)[1:]


fig = plt.figure()
ax0 = fig.add_subplot(221)
waterFlowS12.plot(ax=ax0)

ax1=fig.add_subplot(222)
sm.graphics.tsa.plot_acf(waterFlowS12, lags=nlag, ax=ax1)
plt.show()

fig = plt.figure()
ax0 = fig.add_subplot(221)
sm.graphics.tsa.plot_acf(waterFlowS12d1, ax=ax0, lags=48)
ax1 = fig.add_subplot(222)
sm.graphics.tsa.plot_pacf(waterFlowS12d1, ax=ax1, lags=48)
plt.show()

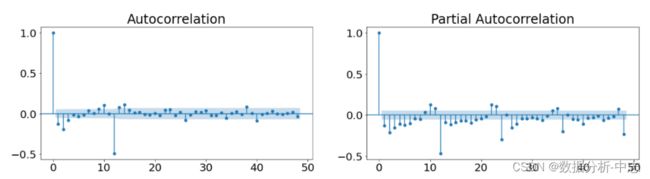
通过1阶差分后构造数据的ACF图和PACF图，通过上图可以告诉我们有怎样的滞后项。确定完毕相关的参数后，开始采用StatsModels中的状态空间对模型进行拟合。

# Build SARIMA
arima_order1=(0,1,0)
season_order1=(0,1,1,12)
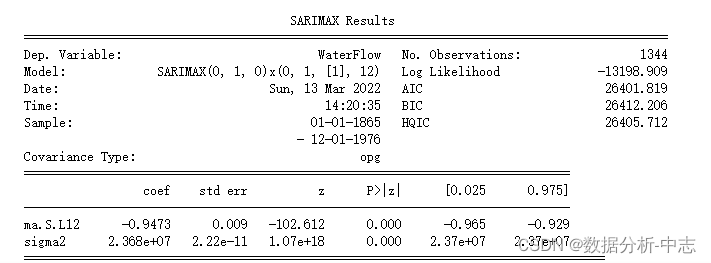
mod1 = sm.tsa.statespace.SARIMAX(train, trend='n', order=arima_order1, seasonal_order=season_order1).fit()
pred=mod1.predict()
print(mod1.summary())

模型拟合效果展示：

# check validation results
subtrain = train['1960':'1970']
MAPE = (np.abs(train-pred)/train).mean()
subMAPE = (np.abs(subtrain-pred['1960':'1970'])/train).mean()

fig = plt.figure()
ax0 = fig.add_subplot(211)
plt.plot(pred, label='Fitted');
plt.plot(train, color='red', label='Original')
plt.legend(loc='best')
plt.title("SARIMA %s%s Model, MAPE = %.4f" % (arima_order1, season_order1, MAPE))

ax1 = fig.add_subplot(212)
plt.plot(pred['1960':'1970'], label='Fitted');
plt.plot(subtrain, color='red', label='Original')
plt.legend(loc='best')
plt.title("Details from 1960 to 1970, MAPE = %.4f" % subMAPE)
plt.show()

模型结果展示：

# test alternatives
arima_order2 = (1,1,1)
season_order2 = (0,1,1,12)
mod2 = sm.tsa.statespace.SARIMAX(train, trend='n', order=arima_order, seasonal_order=season_order).fit()
forecast1 = mod1.predict(start = '1976-12-01', end='1978' , dynamic= True)
forecast2 = mod2.predict(start = '1976-12-01', end='1978' , dynamic= True)
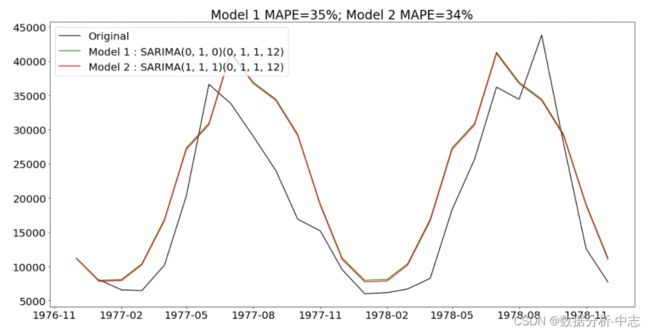
MAPE1 = ((test-forecast1).abs() / test).mean()*100
MAPE2 = ((test-forecast2).abs() / test).mean()*100

plt.plot(test, color='black', label='Original')
plt.plot(forecast1, color='green', label='Model 1 : SARIMA'+ str(arima_order1) + str(season_order1))
plt.plot(forecast2, color='red', label='Model 2 : SARIMA'+ str(arima_order2) + str(season_order2))
plt.legend(loc='best')
plt.title('Model 1 MAPE=%.f%%; Model 2 MAPE=%.f%%'%(MAPE1, MAPE2))

最后，我们看到这两个模型参数的结果几乎重合，二者没有根本的差别。