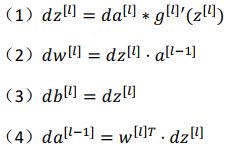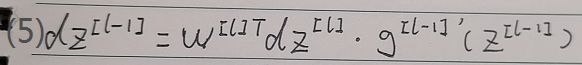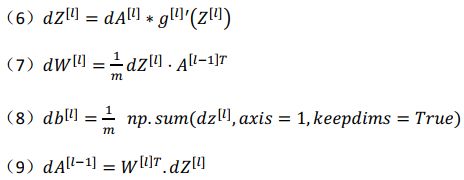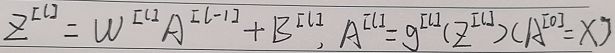深度学习-吴恩达-笔记-4-深层神经网络
目录
深层神经网络
前向传播和反向传播
深层网络中的前向传播
核对矩阵的维数
为什么使用深层表示
搭建神经网络块
参数 VS 超参数
深度学习和大脑的关联性
【此为本人学习吴恩达的深度学习课程的笔记记录，有错误请指出！】
深层神经网络
有一个隐藏层的神经网络，就是一个两层神经网络。神经网络的层数不包含输入层，只包含隐藏层和输出层。
深度学习的符号定义：
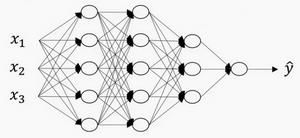
上图是一个四层的神经网络，有三个隐藏层， 输入层是第 0 层。
L 表示层数， 输入层的索引为“0”。
第一个隐藏层 
，表示有 5个隐藏神经元。
输入层 
。
记作 层激活后结果。
记作 层计算 
值的权重。
输入的特征记作 ，但是 同样也是 0 层的激活函数，所以 
。
前向传播和反向传播
前向传播的步骤：
向量化前向传播过程：
前向传播需要喂入 
也就是 ，来初始化，初始化的是第一层的输入值。 
对应于一个训练样本的输入特征，而 
对应于一整个训练样本的输入特征，所以这就是这条链的第一个前向函数的输入，重复这个步骤就可以从左到右计算前向传播。
反向传播的步骤：
反向传播的步骤：
向量化反向传播过程：
深层网络中的前向传播
一个训练样本 x 如何应用前向传播，之后讨论向量化的版本。
第一层需要计算：
第二层需要计算：
以此类推，第四层需要计算：
前向传播可以归纳为多次迭代：
向量化实现过程可以写成：
这里只用一个显式 for 循环， 从 1 到 ，然后一层接着一层去计算。
核对矩阵的维数
当实现深度神经网络的时候，检查代码是否有错的方法就是拿出一张纸过一遍算法中矩阵的维数。
的维度是（下一层的维数，前一层的维数），即： 
的维度是（下一层的维数， 1），即： 
， 且 
[] 和 [] 维度相同， [] 和 [] 维度相同，且 和 向量化维度不变，但 , 以及 的维度会向量化后发生变化。
向量化后：
[]可以看成由每一个单独的[]叠加而得到， [] = ([][1]， [][2]， [][3]， … ， [][])，
为训练集大小，所以 [] 的维度不再是([], 1)，而是([], )。
在做深度神经网络的反向传播时，一定要确认所有的矩阵维数是前后一致的，可以大大提高代码通过率。
为什么使用深层表示
在深度神经网络中，较早的前几层能学习一些低层次的简单特征，等到后几层，就能把简单的特征结合起来，去探测更加复杂的东西。
深层神经网络的特点：
Small：隐藏单元的数量相对较少
Deep：隐藏层数目比较多
深层的网络隐藏单元数量相对较少，隐藏层数目较多，如果浅层的网络想要达到同样的计算结果则需要指数级增长的单元数量才能达到。
另外一个，关于神经网络为何有效的理论，来源于电路理论，如基本逻辑门，譬如与门、或门、非门。对于一个复杂的逻辑运算，如多个变量异或运算，用多层隐藏层就很容易表示异或的运算过程，如果非要用单层隐藏层，那么需要在一层中例举异或计算中出现的各种可能性，导致隐藏单元的数量呈指数增长。
建议：开始解决一个新问题时，通常会从 logistic 回归开始，再试试一到两个隐层，把隐藏层数量当作参数、超参数一样去调试，这样去找比较合适的深度。
搭建神经网络块
神经网络的每一步训练包含了，从 [0] 开始，也就是 然后经过一系列正向传播计算得到输出值 
，之后再用输出值和真实值计算误差，最后实现反向传播计算每一层的参数 
和 
。
这里有一个细节， 那就是把正向传播过程计算出来的 值缓存下来，在反向传播的计算过程中，利用缓存的 值进行对参数求导，可以迅速得到 
和 
。
参数 VS 超参数
参数：权重（ ）、偏差（ ）
超参数： learning rate （学习率）、 iterations(梯度下降法迭代次数)、 （隐藏层数目）、 
（隐藏层单元数目）、 choice of activation function（激活函数的选择）等。 这些数字实际上控制了最后的参数 和 的值，所以它们被称作超参数。
实际上深度学习有很多不同的超参数，之后我们也会介绍一些其他的超参数，如 momentum、 mini batch size（小批量大小）、regularization parameters（正则化参数） 等等。
如何寻找超参数的最优值？
有一条经验规律：不断地尝试不同的超参数，并且尝试交叉检验或类似的检验方法，然后挑一个对你的问题效果比较好的数值。
这可能是深度学习比较让人不满的一部分，也就是你必须尝试很多次不同可能性，或许以后会有更好的方法来找到超参数。
深度学习和大脑的关联性
深度学习和大脑有什么关联性吗？ 答案是： 关联不大。
深度学习像大脑这样的类比其实是过度简化了大脑具体在做什么，但因为这种形式很简洁，也能让普通人更愿意公开讨论，也方便新闻报道并且吸引大众眼球，但这个类比是非常不准确的。至今为止其实连神经科学家们都很难解释，究竟一个神经元能做什么。