Pytorch实现经典卷积神经网络LeNet
Pytorch实现经典卷积神经网络LeNet
- LeNet
- 模型训练
- d2l库中常用函数介绍
LeNet
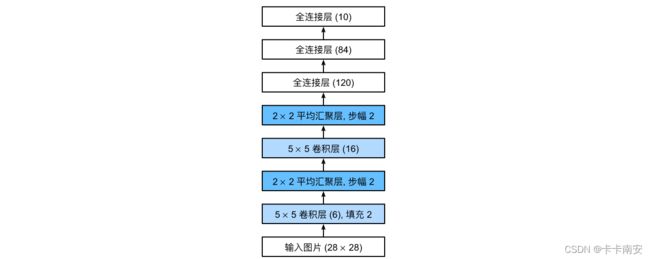
总体来看,LeNet(LeNet-5)由两个部分组成:
- 卷积编码器:由两个卷积层组成;
- 全连接层密集块:由三个全连接层组成。

每个卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层(即池化层)。请注意,虽然ReLU和最大汇聚层更有效,但它们在20世纪90年代还没有出现。每个卷积层使用5×5卷积核和一个sigmoid激活函数。这些层将输入映射到多个二维特征输出,通常同时增加通道的数量。第一卷积层有6个输出通道,而第二个卷积层有16个输出通道。每个2×2池化操作通过空间下采样将维数减少4倍。卷积的输出形状由批量大小、通道数、高度、宽度决定。

为了将卷积块的输出传递给密集块,我们必须在小批量中展平每个样本。换言之,我们将这个四维输入转换成全连接层所期望的二维输入。这里的二维表示的第一个维度索引小批量中的样本,第二个维度给出每个样本的平面向量表示。LeNet的密集块有三个全连接层,分别有120、84和10个输出。因为我们在执行分类任务,所以输出层的10维对应于最后输出结果的数量。
模型的搭建程序如下所示:
import torch
from torch import nn
from d2l import torch as d2l
class Reshape(torch.nn.Module):
def forward(self, x):
return x.view(-1, 1, 28, 28)
net = nn.Sequential(
Reshape(),
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
下面,我们将一个大小为28×28的单通道(黑白)图像通过LeNet。通过在每一层打印输出的形状来查模型是否符合期望:
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape: \t',X.shape)
输出:
Conv2d output shape: torch.Size([1, 6, 28, 28])
Sigmoid output shape: torch.Size([1, 6, 28, 28])
AvgPool2d output shape: torch.Size([1, 6, 14, 14])
Conv2d output shape: torch.Size([1, 16, 10, 10])
Sigmoid output shape: torch.Size([1, 16, 10, 10])
AvgPool2d output shape: torch.Size([1, 16, 5, 5])
Flatten output shape: torch.Size([1, 400])
Linear output shape: torch.Size([1, 120])
Sigmoid output shape: torch.Size([1, 120])
Linear output shape: torch.Size([1, 84])
Sigmoid output shape: torch.Size([1, 84])
Linear output shape: torch.Size([1, 10])
请注意,在整个卷积块中,与上一层相比,每一层特征的高度和宽度都减小了。 第一个卷积层使用2个像素的填充,来补偿 5×55×5 卷积核导致的特征减少。 相反,第二个卷积层没有填充,因此高度和宽度都减少了4个像素。 随着层叠的上升,通道的数量从输入时的1个,增加到第一个卷积层之后的6个,再到第二个卷积层之后的16个。 同时,每个池化层的高度和宽度都减半。最后,每个全连接层减少维数,最终输出一个维数与结果分类数相匹配的输出。
模型训练
首先我们先加载数据集并定义好训练函数:
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
"""使用GPU计算模型在数据集上的精度"""
if isinstance(net, nn.Module):
net.eval() # 设置为评估模式
if not device:
device = next(iter(net.parameters())).device
# 正确预测的数量,总预测的数量
metric = d2l.Accumulator(2)
with torch.no_grad():
for X, y in data_iter:
if isinstance(X, list):
# BERT微调所需的(之后将介绍)
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
metric.add(d2l.accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
#@save
def train(net, train_iter, test_iter, num_epochs, lr, device):
"""用GPU训练模型(在第六章定义)"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,样本数
metric = d2l.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
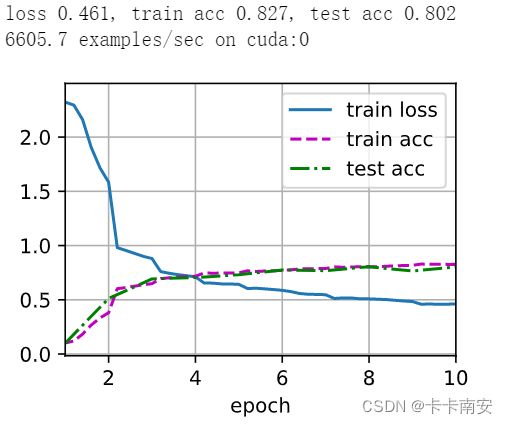
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')
下面我们开始训练和评估:
lr, num_epochs = 0.9, 10
train(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l库中常用函数介绍
在这次示例中我们用到了很多dl2库中封装好的函数,这个库是《动手学深度学习》中配套的学习库,这里面封装了训练、可视化等常用函数和类,在这里我们简单介绍一下这次示例中用到的几个。
1.load_data_fashion_mnist(batch_size, resize=None)
def load_data_fashion_mnist(batch_size, resize=None):
"""Download the Fashion-MNIST dataset and then load it into memory."""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="../data",
train=True,
transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="../data",
train=False,
transform=trans,
download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers()),
data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=get_dataloader_workers()))
这个数据集比较简单,就是获取mnist手写数字数据集和训练集的dataloader用于后续的训练和测试。
2.accuracy(y_hat, y)
def accuracy(y_hat, y):
"""Compute the number of correct predictions."""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = d2l.argmax(y_hat, axis=1)
cmp = d2l.astype(y_hat, y.dtype) == y
return float(d2l.reduce_sum(d2l.astype(cmp, y.dtype)))
这个函数用于在图像分类中判断网络的预测值与真实值是否相同,相同则返回1,不同则返回0,函数的输入分别是网络预测的输出和图像分类的标签,例如d2l.accuracy(net(X), y)。
3.Accumulator类
class Accumulator:
"""For accumulating sums over `n` variables."""
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
这是一个用于存储数据的类,实例化的输入是你想存储的浮点数的个数。例如在这个示例中,我们想存储预测正确的数量和总预测的数量,所以我们实例化为metric = d2l.Accumulator(2)。
当我们调用.add函数时,即可在原先值的基础上加上新输入的值,.add函数输入的个数与前面初始化时定义的个数相同,例如metric.add(d2l.accuracy(net(X), y), y.numel())。
在取出数据时我们只需要给出对应的索引即可,例如在此示例中,metric[0]代表预测正确的数量,metric[1]代表总预测的数量,令metric[0]/metric[1]即可得出预测正确的比例。
4.Animator类
class Animator:
"""For plotting data in animation."""
def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
figsize=(3.5, 2.5)):
# Incrementally plot multiple lines
if legend is None:
legend = []
d2l.use_svg_display()
self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
if nrows * ncols == 1:
self.axes = [self.axes,]
# Use a lambda function to capture arguments
self.config_axes = lambda: d2l.set_axes(self.axes[
0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
self.X, self.Y, self.fmts = None, None, fmts
def add(self, x, y):
# Add multiple data points into the figure
if not hasattr(y, "__len__"):
y = [y]
n = len(y)
if not hasattr(x, "__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i, (a, b) in enumerate(zip(x, y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x, y, fmt in zip(self.X, self.Y, self.fmts):
self.axes[0].plot(x, y, fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
这是一个用于可视化数据曲线的类,实例化的输入包括x和y轴的标题(xlabel&ylabel)、图例(legend)、x和y轴的单位(xscale&yscale)、x和y轴的取值范围(xlim&ylim)、图片的大小(figsize)等。例如在此示例中,我们想要观察训练损失、训练时的正确率和测试集的正确率三条曲线,因此我们可以实例化为animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], legend=['train loss', 'train acc', 'test acc'])。
调用.add函数即可将我们想要可视化的数据输出到图像上,.add函数的输入是数据的横纵坐标x和y,其中输入x为单个值,输入y可以是单个值也可以是一个元组或列表,长度与legend长度一致,没有数据时用None代替。例如:
animator = d2l.Animator(xlabel='epoch', xlim=[1, 5],
legend=['train loss', 'train acc', 'test acc'])
for i in range(6):
animator.add(i, [1,2,3])
输出为:
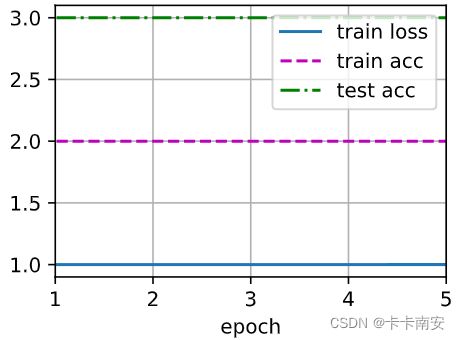
在此示例中,我们想要观察训练损失、训练时的正确率和测试集的正确率三条曲线,因此我们在训练时调用
animator.add(epoch + (i + 1) / num_batches, (train_l, train_acc, None))
在测试时调用animator.add(epoch + 1, (None, None, test_acc)),三条曲线将被画在同一张图里。
5.try_gpu(i=0)
def try_gpu(i=0):
"""Return gpu(i) if exists, otherwise return cpu()."""
if torch.cuda.device_count() >= i + 1:
return torch.device(f'cuda:{i}')
return torch.device('cpu')
检测是否有gpu,如果有则返回gpu设备,没有则返回cpu,常于net.to(device)、X.to(device)、 y.to(device)等配合使用。
6.time类
class Timer:
"""Record multiple running times."""
def __init__(self):
self.times = []
self.start()
def start(self):
"""Start the timer."""
self.tik = time.time()
def stop(self):
"""Stop the timer and record the time in a list."""
self.times.append(time.time() - self.tik)
return self.times[-1]
def avg(self):
"""Return the average time."""
return sum(self.times) / len(self.times)
def sum(self):
"""Return the sum of time."""
return sum(self.times)
def cumsum(self):
"""Return the accumulated time."""
return np.array(self.times).cumsum().tolist()
- start:记录当前时间
- stop:返回经过的时间,即stop-start
- avg:返回所有经过的时间的平均值
- sum:返回所有经过的时间的总和
- cumsum:返回一个列表,列表中第n个元素为第n-1个元素的值加上第n段时间的和,即前面所有累积的时间和