【算法】离散傅里叶变换(DFT)
- 真实的系统是会离散的,时变的。理想者将瞬时态看成时线性的系统,将时变系统分成了不同阶段。离散在围观层面是连续的,但从表层感受时,变化是迅猛的,可以忽略不计变化的过程,因而成为了离散。
一、离散系统
离散控制系统是指在控制系统的一处或数处信号为脉冲序列或数码的系统。如果在系统中使用了采样开关,将连续信号转变为脉冲序列去控制系统,则称此系统为采样控制系统。如果在系统中采用了数字计算机或数字控制器,其信号是以数码形式传递的,则称此系统为数字控制系统。通常把采样控制系统和数字控制系统统称为离散控制系统。离散系统与连续系统相比,既有本质上的不同,又有分析研究方面的相似性。
利用z变换法研究离散系统,可以把连续系统中的许多概念和方法推广应用于离散系统。目前,离散系统的最广泛应用形式是以数字计算机,特别是以微型计算机为控制器的数字控制系统。也就是说,数字控制系统是一种以数字计算机为控制器去控制具有连续工作状态的被控对象的闭环控制系统。因此,数字控制系统包括工作于离散状态下的数字计算机和工作于连续状态下的被控对象两大部分。
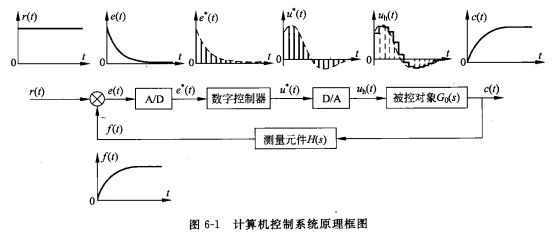
图6-1给出了数字控制系统的原理框图。图中,计算机作为校正装置被引进系统,它只能接受时间上离散、数值上被量化的数码信号。而系统的被控量c(t)、给定量r(t)一般在时间上是连续的模拟信号。因此要将这样的信号送入计算机运算,就必须先把偏差量e(1)用采样开关在时间上离散化,再由模数转换器(A/D)将其在每个离散点上进行量化,转换成数码信号,这两项工作一般都由A/D来完成,然后进人计算机进行数字运算,输出的仍然是时间上离散、数值上量化的数码信号。数码信号不能直接作用于被控对象,因为在两个离散点之间是没有信号的,必须在离散点之间补上输出信号值。一般可采用保持器的办法。最简单的保持器是零阶保持器,它将前一个采样点的值一直保持到后一个采样点出现之前,因此其输出是阶梯状的连续信号(如图6-1中信号u(t)),作用到被控对象上(RS触发器)。数模转换和信号保持都是由数模转换器(D/A)完成的。
1 信号的采样与保持
采样器与保持器是离散系统的两个基本环节,为了定量研究离散系统,必须用数学方法对信号的采样过程和保持过程加以描述。
在采样过程中,把连续信号转换成脉冲或数码序列的过程,称作采样过程。实现采样的装置,叫做采样开关或采样器。如果采样开关以周期T时间闭合,并且闭合的时间为r,这样就把一个连续函数e(t)变成了一个断续的脉冲序列e" (t),如图6-3(b)所示。
这就是香农(Shannon)采样定理。采样定理说明,当采样频率大于或等于信号所含最高频率的两倍时,才有可能通过理想滤波器,把原信号完整地恢复出来。否则会发生频率混叠(如图6-5©所示),此时即使使用理想滤波器,也无法将主频谱分离出来,因而不可能准确复现原有的连续信号。

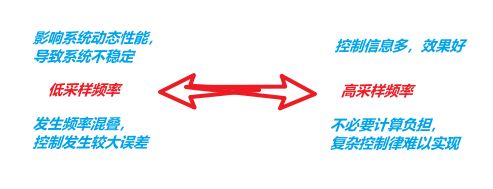
采样周期T是离散控制系统设计中的一个重要因素。采样定理只给出了不产生频率混叠时采样周期T的最大值(或采样角频率w,的最小值),显然,T选得越小,即采样角频率w,选得越高,获得的控制过程的信息便越多,控制效果也会越好。但是,如果T选得过短,将增加不必要的计算负担,难以实现较复杂的控制律。反之,T选得过长,会给控制过程带来较大的误差,影响系统的动态性能,甚至导致系统不稳定。因此,采样周期T要依据实际情况综合考虑,合理选择。
2 Z变换
拉普拉斯变换是研究线性定常连续系统的基本数学工具,而z变换则是研究线性定常离散系统的基本数学工具。z变换是在离散信号拉普拉斯变换基础上,经过变量代换引申出来的一种变换方法。
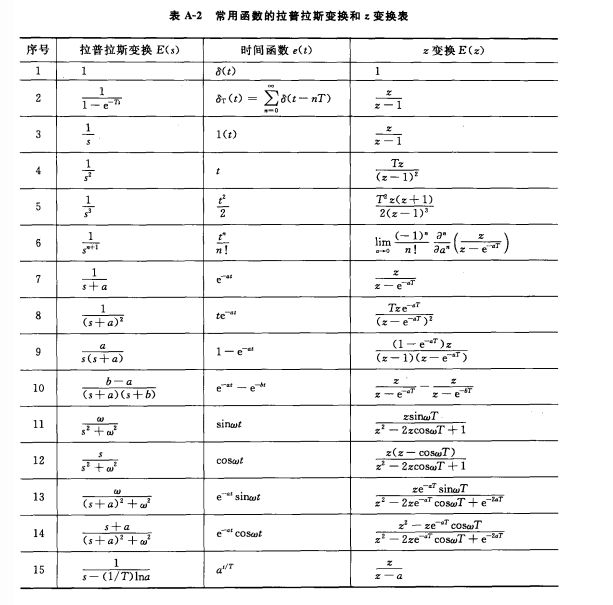
傅里叶方法通常用于信号分析和系统设计。在我们的案例中,这种方法主要用于SMPC电压分析。利用数字示波器(最大采样数N =10.000)采样电压,利用Matlab[13]离线计算离散傅里叶变换(DFT)。为了得到DFT,对离散时间傅里叶变换(DFT)的连续频域进行N个采样,在z平面的单位圆上均匀间隔N个点,即在点[w] = (2πk/N), k = 0,1,…, N - 1,如(2)所示。信号s[N]要么是长度为N的有限长度序列,要么是周期为N的周期序列。
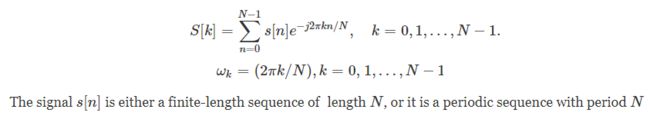
二、傅里叶变换的局限性

由于时间上要求了无限,频率和时间上要求了不间断连续,这在时间上和空间上都无法做到采样。 离散时间傅立叶变换并没有摆脱无穷大 1 和 2,但它确实消除了无穷大 3。
三、离散时间傅立叶变换(DTFT)
离散时间傅立叶变换(DTFT)
DTFT计算公式,中的w取值是连续的而且从负无穷大到正无穷大,对于计算机处理是不可能的,需要无限细分无限区间。即使在DTFT小节中用matlab实现计算,也只是将(-pi,pi)区间划分成1600份来逼近DTFT的效果。

实际上真正用的是DFT,离散傅里叶变换。离散傅里叶变换可以将连续的频谱转化成离散的频谱去计算,这样就易于计算机编程实现傅里叶变换的计算。FFT算法的出现,使得DFT的计算速度更快。
离散时间极大地减少了记录信号所需的无数次测量。不是在每个时间点都测量信号,而是在其持续时间内仅测量信号有限的次数

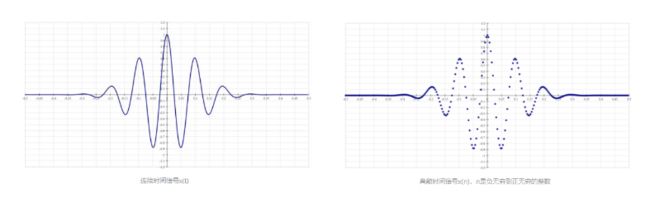
为了尝试了解 DTFT 的工作原理,对给定离散时间信号执行 DTFT。由于 DTFT 中还有一些无穷大,这里做一些简化DTFT 要求测试无数个频率。资源有限,只测试一个频率:10Hz。
DTFT 在整个时间段内查看信号。资源有限,我使用的信号除下图中包含的短时间外,其他所有时间都为零。
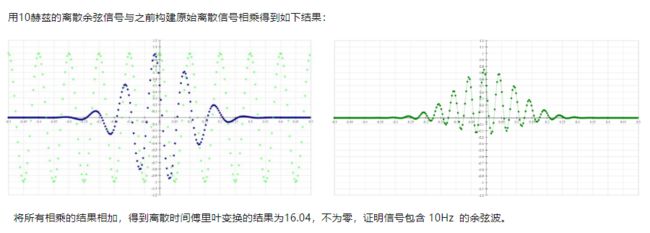
下一阶段将对对正弦波做同样相乘,再累加得到的结果是-27.79,这也不是零,这意味着在该频率处也存在正弦分量。同时这个特定频率具有相移。

该信号包含10Hz的余弦和正弦分量。余弦分量的幅值为 16.04,正弦分量的幅值为 -27.79。因此,信号确实包含频率为 10Hz 的正弦波。知道正弦和余弦的贡献再利用勾股定理,很容易得到10Hz总贡献32.09
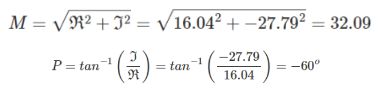
因此,DTFT 为我的问题提供了以下答案:信号中确实存在 10Hz 的正弦波,它的幅值为 32.09,相位为-60°
因此,DTFT 已经在某种程度上将傅立叶变换变成了实用工具。然而,还有两个无穷大需要摆脱。
无限积分—— 信号在整个时间内积分
连续频率——信号由无数个相邻频率组成
三、离散傅里叶变换(DFT)
参考:如何理解离散傅里叶变换DFT----实验数据说话

离散傅里叶变化是对FT变化在区间(0,2*pi)的等间距N点采样
为了将傅里叶变换转换为 DFT,我们必须做出一些妥协,信号必须是离散的。换句话说,我们必须放弃信号中可用的一些信息.
在 DTFT 中,我们仅在某些离散时间点对信号进行采样或测量。现在在 DFT 中,我们也只针对某些离散频率测试信号。这意味着我们将不得不放弃信号中可用的一些频率信息。理想情况下,我们只想放弃我们绝对需要的尽可能多的信息。换句话说,考虑到系统的处理和时间限制,我们希望 DFT 的频率分辨率尽可能大。两个相邻频率之间的步长大小反应了我们频率分辨率。

如果我们对上面的离散采样信号执行DFT,将得到如下图所示的频域图。
这就是香农(Shannon)采样定理。采样定理说明,当采样频率大于或等于信号所含最高频率的两倍时,才有可能通过理想滤波器,把原信号完整地恢复出来。否则会发生频率混叠(如图6-5©所示),此时即使使用理想滤波器,也无法将主频谱分离出来,因而不可能准确复现原有的连续信号。
信号最高频率是2.75。
取采样频率为10Hz。
这个信号不仅包含一组 10Hz 左右的频率,还有一个在 190Hz 左右。事实上,更高频率的波峰甚至更多,只是,DFT 不会测试高于采样频率的频率。我们称这些是鬼频率,根本不存在于信号中,而是一种数学上的问题。它们的出现是因为我们掌握的有关信号的信息存在空白。信号被采样,这意味着它仅在某些时间点定义。因此,只要较高频率的正弦波在信号定义的那些时间点达到正确的值,那么 DTFT 和 DFT 都会认为这些频率存在于信号中,就像这样:
在对信号进行采样时,若不想丢失太多信息,则必须以至少两倍于信号中最高频率的频率对其进行采样。例如对于语音信息,需要每秒至少对声音信号进行 40,000 次(40kHz)采样,这是因为我们的耳朵可以检测到的最高频率是 20kHz。
例如pwm信号是400kHz,则采样信号至少两倍于信号中最高频率的频率对其进行采样,为800kHz,每秒至少对声音信号进行 800,000 次(800kHz)采样。
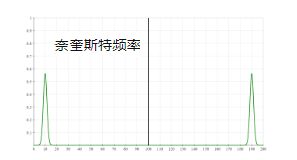
回到上面的 DFT 产生的频率图,这次我在 100Hz 处画了一条黑线,被称为奈奎斯特频率的对称就点位于黑线所在的 100Hz 处。至于奈奎斯特频率后续可以专门出一篇文章来讲,另外还有混叠,随着降低采样频率,每秒测量信号的次数越来越少。因此,我们正在丢失越来越多的信号的信息。奈奎斯特频率始终是采样频率的一半,它越来越接近信号中的最高频率。在大约 30Hz 的采样率下,奈奎斯特频率会碰到 10Hz 的频率组,我们从信号中丢失了太多信息。结果,信号开始失真。这种失真称为混叠。
( 190 + 10 ) / 2 = 100 H z (190+10)/2=100Hz (190+10)/2=100Hz
这个信号不仅包含一组 10Hz 左右的频率,还有一个在 190Hz 左右。事实上,更高频率的波峰甚至更多,只是,DFT 不会测试高于采样频率的频率。我们称这些是鬼频率,根本不存在于信号中,而是一种数学上的问题。它们的出现是因为我们掌握的有关信号的信息存在空白。信号被采样,这意味着它仅在某些时间点定义。因此,只要较高频率的正弦波在信号定义的那些时间点达到正确的值,那么 DTFT 和 DFT 都会认为这些频率存在于信号中,就像这样:
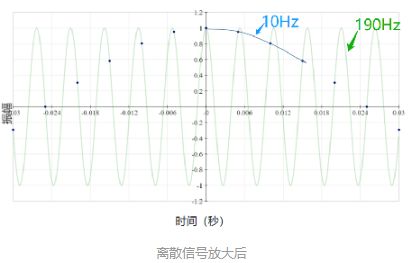
回到上面的 DFT 产生的频率图,这次我在 100Hz 处画了一条黑线,被称为奈奎斯特频率的对称就点位于黑线所在的 100Hz 处。至于奈奎斯特频率后续可以专门出一篇文章来讲,另外还有混叠,随着降低采样频率,每秒测量信号的次数越来越少。因此,我们正在丢失越来越多的信号的信息。奈奎斯特频率始终是采样频率的一半,它越来越接近信号中的最高频率。在大约 30Hz 的采样率下,奈奎斯特频率会碰到 10Hz 的频率组,我们从信号中丢失了太多信息。结果,信号开始失真。这种失真称为混叠。

采样频率分布范围:
f / N ∗ k f/N*k f/N∗k

参考文献
深入理解离散傅里叶变换(DFT)
但是在工程应用中,得益于数字技术的应用,绝大多数傅里叶变换的应用都是采用离散傅里叶变换(DFT),更确切的说,是它的快速算法FFT。这篇文章再来写写有关离散傅里叶变换的关键点。
这篇属于纯理论推导,全是公式。
参考:离散傅里叶变换(DFT)
这篇实践性比较强,用matlab分析。
DTFT计算公式,中的w取值是连续的而且从负无穷大到正无穷大,对于计算机处理是不可能的,需要无限细分无限区间。即使在DTFT小节中用matlab实现计算,也只是将(-pi,pi)区间划分成1600份来逼近DTFT的效果。
实际上真正用的是DFT,离散傅里叶变换。离散傅里叶变换可以将连续的频谱转化成离散的频谱去计算,这样就易于计算机编程实现傅里叶变换的计算。FFT算法的出现,使得DFT的计算速度更快。
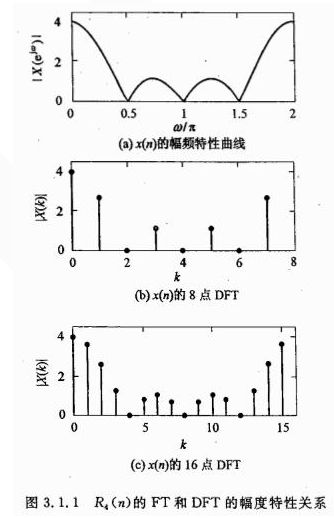
说明:上图结果证明了离散傅里叶变化是对FT变化在区间(0,2*pi)的等间距N点采样
四、窗函数与频谱泄露-STFT短时傅里叶变换
参考:动手实践–窗函数与频谱泄漏
在上一篇文章中,离散傅里叶变换 (DFT)为我们提供了一种实际实现傅里叶变换的实用方法。然而,为了分析长信号,经常需要将它们分解成更小的块,并在每个块上运行 DFT,一次一个。正如我们将很快看到的,这可能会导致称为频谱泄漏的问题。一个我们无法完全解决的问题。但是,可以通过使用窗口函数来降低其严重性。
窗函数是在信号通过 DFT 算法发送之前改变信号形状的函数。以这样一种方式预处理信号,将其切成小块的时候,使其频谱影响尽可能小。
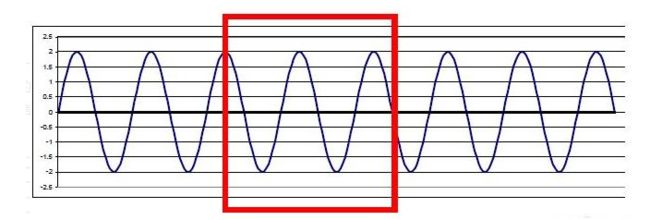
在上一篇文章中,我们分析了人工合成信号,如下所示,该信号在我们的区块开始时从零开始,并在我们的区块结束之前趋于零。这样的信号不需要加窗函数。然而,并不是所有的信号都那么方便。事实上,几乎所有日常信号在我们对它们运行 DFT 之前都需要使用窗口函数进行一些调节。想象一下,你正在使用一个录音软件来写一封信。计算机通过分析您说话时声音中的频率模式来识别您所说的内容。每种声音都有自己独特的频率模式。计算机分析每个模式并将其与存储在内存中的字典中包含的单词相关联。录音时,你肯定不会一个个字的单独发音,来帮助计算机识别各个声音。因此,计算机会不断地记录你的声音,而且会不断地将此记录分成块并将每个块发送出去进行处理。
频谱泄漏:相同的信号显示出非常不同的频率响应。但是,这怎么可能?我们没有改变信号本身,我们只是缩短了每个块的长度。我们在第一张图中看到的峰值的频率分量已被压缩,它们的一些能量已经泄漏到相邻的频率中,这是频谱泄漏。
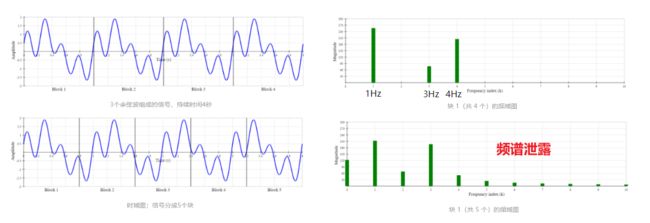
窗函数如何减少频谱泄漏:
首先看从傅里叶级数到傅里叶变换,产生了哪些变化
DFT 已经取消了这些变化,因为我们无法应对它们造成的无穷大。所以基本上,我们正在使用一个与傅里叶级数非常相似的工具,它只能对重复信号进行建模,来尝试对非重复信号进行建模。这就是为什么我特意选择一个重复信号来演示频谱泄漏现象的原因,对于重复信号,只有在正确的位置拆分它才知道真正发生了重复
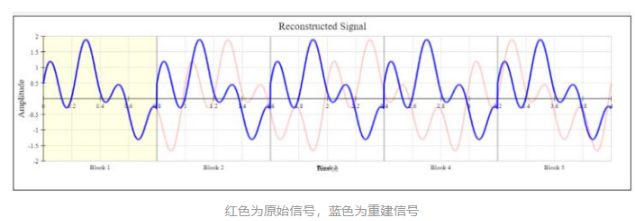
当我尝试用余弦波重构整个信号时,以蓝色显示的重构信号不再类似于原始信号,事实上,重建信号成功模仿原始信号的唯一一次是在我们正在处理的实际块期间。这就是你在所选块Block1中看不到红色信号的原因,重建的信号覆盖了它。每个块之间的信号存在不连续性,正是这些不连续性导致了频谱泄漏。当信号试图快速重新调整到它认为它应该在下一个块开始的位置时,信号的一些能量正在泄漏到更高的频率中。
块之间的这种不连续性正是发明窗口函数要解决的问题。它们不能完全恢复原始信号的频率响应,但可以大大减少频谱泄漏到更高频率的分量。有许多不同类型的窗口函数,**但是,它们都有一个共同的目标,确保信号在块的开头和结尾处为零或几乎为零。**为了应用窗口,时域信号的每个点都乘以相应的窗口系数。因此,如果有块中的信号样本,还必须有窗口函数中的系数。让我们看几个例子。
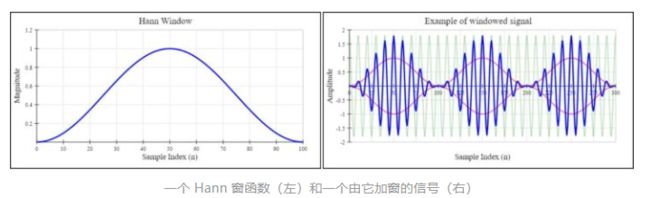
Hann 窗函数
以 奥地利气象学家Julius Ferdinand von Hann (1839 – 1921) 的名字命名。他发明了一种加权移动平均技术,用于结合邻近地区的气象数据。他的技术后来被Blackman 和 Tukey用来推导 Hann 窗口函数,如下图左图所示。
Hamming窗函数
汉明窗函数是由Richard Hamming (1915 – 1998) 发明的。它的形状与汉窗相似,但有一个重要区别。汉明窗完全淡出信号,而汉明窗在块的开始和结束处留下一点信号
为什么块的开头和结尾处不能有零样本
Bartlett窗函数
Bartlett 窗函数由英国统计学家Maurice Stevenson Bartlett(1910 – 2002) 发明,是一个三角形窗。
Tukey 窗函数
Tukey 窗口函数以其发明者的名字命名:John Wilder Tukey(1915 – 2000)。我们已经在上面提到了 Tukey,因为他与 Blackman 一起开发了 Hann 窗口。这也不是我们最后一次见到他,与 James Cooley 一起,他发明了Cooley-Tukey FFT 算法
窗函数的应用:
对于不同信号使用的最佳窗口函数的问题有点复杂,这取决于将信号 DFT 处理到频域后打算如何处理它。例如,如果想在上面讨论的频域中执行某些操作后恢复时域信号,那么汉明窗可能是最好的。
但是,在下面的模拟中,可以比较不同的窗口函数,并查看它们对频域信号的影响。需要特别注意的是它们如何减少频谱泄漏到更高频率。
在将信号分解为 DFT 所需的块之前,加窗函数有助于调节信号。这是为了消除导致频谱泄漏的块之间的不连续性,一些信号的能量泄漏到更高的频率。这些不连续性是由 DFT 看到信号的方式产生的伪影。这是因为它与只能模拟重复信号的傅里叶级数相似。
所以现在,使用 DFT 和窗口函数,终于找到了一种对真实信号执行傅里叶变换的方法。但是,DFT 可能会占用大量处理器资源,尤其是在一个块中有大量样本的情况下。我们能做些什么来提高 DFT 的效率吗?
在接下来的文章中,将介绍快速傅里叶变换,记得点赞加关注哦!
五、FFT算法——(DFT)的加速
参考:推导FFT算法的本质-单位圆求逆来加快算法。
参考:彻底搞懂快速傅里叶变换FFT核心思想–分而治之
前面几篇文章中使用离散傅里叶变换和窗函数,实现了对真实世界信号执行傅里叶变换。然而,**及时是处理持续非常短的信号的计算量也可能非常大。**但是,如果采用一种为“分而治之”的方法来分解问题,就可以大大减少这个计算量。
分而治之是快速傅里叶变换 (FFT) 的核心。FFT 算法最初发表在 1965 年的一篇名为An Algorithm for the Machine Calculation of Complex Fourier Series 的论文中。它由 IBM 的研究员 James Cooley和普林斯顿大学的教授John Tukey编写。
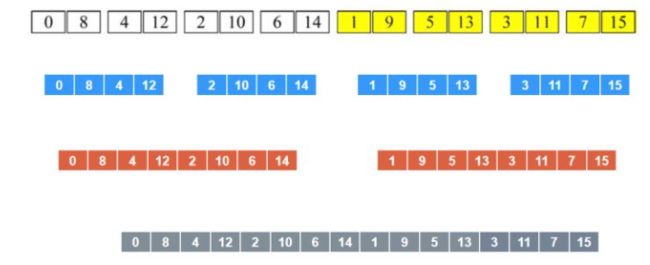
首先考虑一个与傅里叶变换无关的简单问题。对于一个包含 16 个数字的列表,找出列表中最大的数字。
一般我们按顺序遍历,依次比较验证这16个数,哪个是最大的,根据列表的数量、以及最大数字所在实际位置,这个问题就变得比较繁琐了。
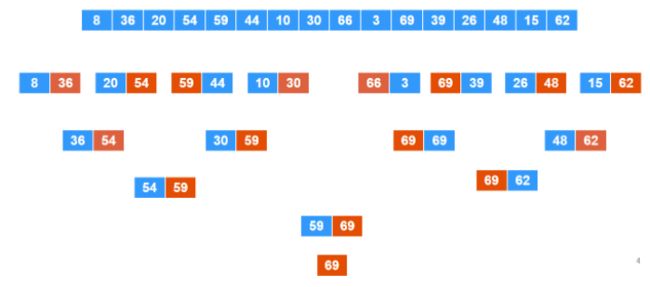
一种更快的方法是将问题分成越来越小的块,直到问题变得非常小,解决起来很简单,这就是“分而治之”的由来。因此,将 16 个值的列表分成 2 组,每组 8 个。上面列表中的前 8 个值将形成第一组,最后 8 个值将形成第二组,…然后再次分成 8 组,每组 2 个值。

然后对于这8组数字,依次比较,保留较大的数,然后标记为橙色,直接舍弃掉那个较小的值,直到只剩下一个数字,那就是最大值,这就是分治法,找最大值。总共比较了多少次:8+4+2+1,总共15次, 显然比顺序查找要少得多。
结合分治法的各个阶段,把他应用于傅里叶变换,就有以下三个步骤:
DIVIDE:将样本分成样本总数一半的组,直到每组中只剩下一对样本
CONQUER:每个样本对执行 DFT
COMBINE:使用刚刚执行的计算结果,组合成新样本对,作为下一阶段的输入
重复:不断重复第 2 和第 3 阶段,直到得出一个最终的答案
划分
DFT并不能像上面数字比大小那样直接划分,但是对于周期为T余弦波和正弦波,所以计算DFT的时候,每隔一个周期T,两个点的复指数是相等的,只是信号值x(n)不同,所以我们只需保存第一个周期cos,sin值, DFT的x(k)
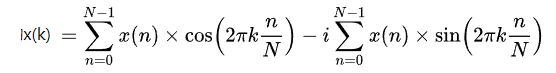
举个例子,下图就是一个周期为2π的余弦波,即时域每隔2π (相应的索引间隔为8),他们的值是相等的,这是第一个结论,可以帮组我们进行分组
另一个结论是随着我们增加余弦波的频率,也会出现周期性,注意目前只观察2个点,索引为0和8的位置(间隔为一个周期的点对)。
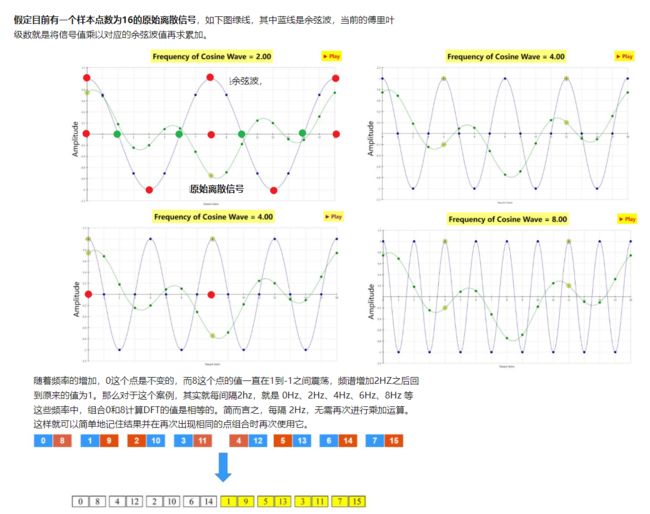
假定目前有一个样本点数为16的原始离散信号,如下图绿线,其中蓝线是余弦波,当前的傅里叶级数就是将信号值乘以对应的余弦波值再求累加。
随着频率的增加,0这个点是不变的,而8这个点的值一直在1到-1之间震荡,频谱增加2HZ之后回到原来的值为1。那么对于这个案例,其实就每间隔2hz,就是 0Hz、2Hz、4Hz、6Hz、8Hz 等这些频率中,组合0和8计算DFT的值是相等的。简而言之,每隔 2Hz,无需再次进行乘加运算。这样就可以简单地记住结果并在再次出现相同的点组合时再次使用它。
对于另外一个点组合4和12,也有如上规律,这一次,重复出现的值发生在 0Hz、4Hz、8Hz 等;简而言之,这个组合结果,每隔 4Hz重复一次,那么我们依次类推还有其他这样的两个点组合,正是通过这种重复利用前期的结果,可以节省计算次数,这也就是快速傅立叶变换快速的原因。
在计算机科学中,分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小,越容易直接求解,解题所需的计算时间也越少。例如,对于n个元素的排序问题,当n=1时,不需任何计算。n=2时,只要作一次比较即可排好序。n=3时只要作3次比较即可,…。而当n较大时,问题就不那么容易处理了。要想直接解决一个规模较大的问题,有时是相当困难的.
目前为止,已经通过分治算法,成功地将整个计算划分为很小的块,至于每个小块如何快速计算,需要参见下一章内容:蝴蝶操作
蝴蝶算法
参考:彻底搞懂快速傅里叶变换FFT–蝴蝶操作
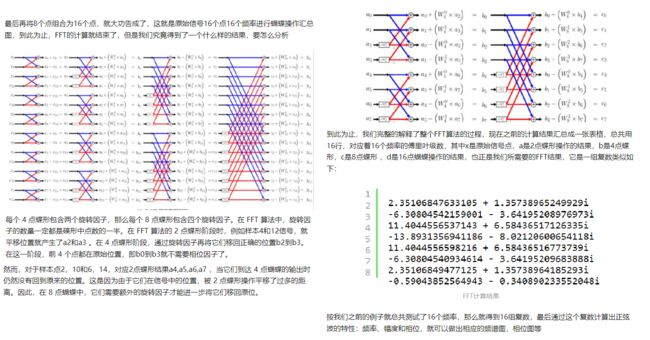
在上一篇文章中,解释了如何使用分治法处理傅里叶变换,以及实现了将信号分解成组序列,每组只包含一对样本,仅对两个样本执行 DFT 是非常简单的,但是为进一步减少计算量,就需要引入蝴蝶图,所谓蝴蝶图,是因为它运算时的形状类似于蝴蝶的翅膀。

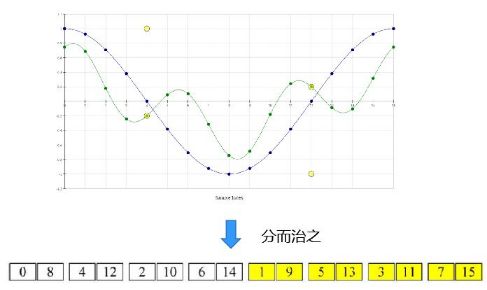
在“划分”阶段结束时,将 16 个样本信号分成 8 个样本对,并以特殊方式对这些对进行排序,如下所示。
蝴蝶操作呢,就是一种联合计算方式,形状类似蝴蝶,运算过程也很简单就像你看到的这样,输入两个值x0和x8分别被重复调用来做运算,只有最下面乘以一个-1,我们分别得到2个结果记作a0,a1。这里的x0、x8分别就是信号索引0和8所对应的值。
旋转因子
参考:彻底搞懂快速傅里叶变换FFT–旋转因子
上一篇文章,引入蝴蝶操作来计算样本对的DFT,实现了“分而治之”中对简单重复小块的处理,同时又引入信号相位改变的新问题,为保持整体的结果不变,利用“旋转因子”将平移后的信号再次平移回去,作为下一阶段的输入。
算法输出
参考: 算法输出
上一篇文章,我们介绍了相位因子,完美解决所有点对的蝴蝶操作,知道了2个样本组合为4个样本点的蝴蝶操作现在留下了四组 4 点蝴蝶,需要将它们组合成两组 8 点蝴蝶,然后组合成一组 16 点蝴蝶,这就最后的结果,FFT 算法的结果就是16 个不同频率正弦波的列表。注意:这里会完成FFT的所有计算,自己动手绘制和计算关键步骤,才能真真搞懂其原理。